Data Structures and Algorithms in Java
6th Edition
ISBN: 9781118771334
Author: Michael T. Goodrich
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5, Problem 16C
In the Towers of Hanoi puzzle, we are given a platform with three pegs, a, b, and c, sticking out of it. On peg a is a stack of n disks, each larger than the next, so that the smallest is on the top and the largest is on the bottom. The puzzle is to move all the disks from peg a to peg c, moving one disk at a time, so that we never place a larger disk on top of a smaller one. See Figure 5.15 for an example of the case n =4. Describe a recursive
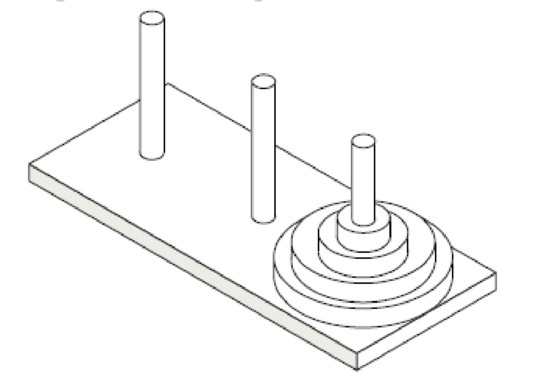
Figure 5.15: An illustration of the Towers of Hanoi puzzle.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Consider a maze represented by a matrix of m rows and n
columns with obstacles (see the figure below). A cell with a
value = -1 is an obstacle that cannot be overcome.
The goal is to start from cell [0, 0] and reach the last cell [m-1,
n-1]. This may be possible by taking several paths. Count the
number of these paths.
The movement is allowed from cells (i+ 1, j) and (i, j+ 1) only.
-1
-1
Provide two solutions, one iterative and one recursive to the
above problem.
Shrek has guessed three positive integers a, b, and c. He keeps these numbers in secret, but he
writes down four numbers on a board in arbitrary order their pairwise sums (three numbers) and sum
of all three numbers (one number). So, there are four numbers on a board in random order: a + b, a+
c, b + c and a+b+c.
You have to guess three numbers a, b, and c using given numbers. Print three guessed integers in any
order. Pay attention that some given numbers a, b and c can be equal (it is also possible that a-b=c).
Instruction: Create a Java program that will perform the algorithm that will solve the problem using
inheritance as shown in the figure. It must satisfy the 3-sample output as shown below. Explain your codes
using comments.
Main class Creates an instance of "Number"
class and call the methods. in
Input
sequence as shown in the figure.
numl, num2, num3, num4 :int
●
Main
Input class - It contains a method in() that ask
four positive integers for the numbers
on the board in…
You are given an instance of a problem where you have an n x n grid
of squares. Each square can be unpainted or can have a hole, so you cannot go
on the square with a hole. The objective is to paint all the squares that do not
have a hole. You start in the square (0,0) which is unpainted. The actions you
can do are: (1) paint the square you are on if it is not painted; (2) move, either
vertically or horizontally, to an adjacent square inside the grid that is not painted
and does not have a hole.
a. Describe a state-space representation for the problem, specifying the
state representation, the initial state, the goal condition, and the actions.
b. Is the state space finite? Is it a tree or a graph?
c. Propose a heuristic for the problem. Is your heuristics admissible or not?
Explain briefly your answer
Chapter 5 Solutions
Data Structures and Algorithms in Java
Ch. 5 - Prob. 1RCh. 5 - Prob. 2RCh. 5 - Prob. 3RCh. 5 - Prob. 4RCh. 5 - Prob. 5RCh. 5 - Draw the recursion trace for the execution of...Ch. 5 - Prob. 7RCh. 5 - Describe a recursive algorithm for converting a...Ch. 5 - Prob. 9RCh. 5 - Prob. 10R
Ch. 5 - Prob. 11CCh. 5 - Prob. 12CCh. 5 - Give a recursive algorithm to compute the product...Ch. 5 - In Section 5.2 we prove by induction that the...Ch. 5 - Write a recursive method that will output all the...Ch. 5 - In the Towers of Hanoi puzzle, we are given a...Ch. 5 - Write a short recursive Java method that takes a...Ch. 5 - Write a short recursive Java method that...Ch. 5 - Use recursion to write a Java method for...Ch. 5 - Write a short recursive Java method that...Ch. 5 - Prob. 21CCh. 5 - Prob. 22CCh. 5 - Prob. 23CCh. 5 - Isabel has an interesting way of summing up the...Ch. 5 - Prob. 25CCh. 5 - Prob. 26CCh. 5 - Prob. 27PCh. 5 - Write a program for solving summation puzzles by...Ch. 5 - Prob. 29PCh. 5 - Write a program that can solve instances of the...
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
What data structure that appeared in COBOL originated with Plankalkl?
Concepts Of Programming Languages
class Box { private: double width; double length: double height: public: Box(double w, l, h) { width = w; le...
Starting Out with C++ from Control Structures to Objects (9th Edition)
When determining whether a number is inside a range, its best to use this operator. a. b. ! c. | | d. ? :
Starting Out with Java: From Control Structures through Objects (7th Edition) (What's New in Computer Science)
Find the no-load value of υo in the circuit shown.
Find υo when RL is 150 Ω.
How much power is dissipated in th...
Electric Circuits. (11th Edition)
What is an object? What is a control?
Starting Out With Visual Basic (8th Edition)
When displaying a Java applet, the browser invokes the _____ to interpret the bytecode into the appropriate mac...
Web Development and Design Foundations with HTML5 (8th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- You are given a stack of unknown number of cards each of which contains one number. Propose an algorithm for finding the average of the numbers on the cards. You may only look at one card at a time. How is this problem different from the previous one?arrow_forwardWrite a program using Python to solve the locker riddle which reads as follows: Imagine 100 lockers numbered 1 to 100 with 100 students lined up in front of those 100lockers:The first student opens every locker.The second student closes every 2nd locker.The 3rd student changes every 3rd locker; if it’s closed, she opens it; if it’s open, she closes it.The 4th student changes every fourth locker (e.g., 4th, 8th, etc.).The 5th student changes every 5th locker (e.g., 5th, 10th, etc.).That same pattern continues for all 100 students. Which lockers are left open after all 100 students have walked the rowof lockers?arrow_forwardIn chess, a walk for a particular piece is a sequence of legal moves for that piece, starting from a square of your choice, that visits every square of the board. A tour is a walk that visits every square only once. (See Figure 5.13.) 5.13 Prove by induction that there exists a knight’s walk of an n-by-n chessboard for any n ≥ 4. (It turns out that knight’s tours exist for all even n ≥ 6, but you don’t need to prove this fact.)arrow_forward
- Write a function find_equivalent_matchings that takes a matching and returns all matchings with the same pattern (including the original one). Using this function, draw all matchings equivalent to {(0, 7), (1, 4), (2, 3), (5, 6)}. You might find it helpful to generate all permutations of a list using itertools.permutation (imported above) as in the following code template. perms=permutations (list_of_items) for p in perms:arrow_forwardThere is a legend about a magical park with N × N trees. The trees are positioned in a square grid with Nrows (numbered from 1 to N from north to south) and N columns (numbered from 1 to N from west to east).The height (in metres) of each tree is an integer between 1 and N × N, inclusive. Magically, the height ofall trees is unique.Bunga is standing on the northmost point of the park and wants to count the number of visible trees for eachcolumn. Similarly, Lestari is standing on the westmost point of the park and wants to count the number ofvisible trees for each row. A tree X is visible if all other trees in front of the tree X are shorter than the treeX.For example, let N = 3 and the height (in metres) of the trees are as follows.6 1 87 5 32 9 4• On the first column, Bunga can see two trees, as the tree on the third row is obstructed by the othertrees.• On the second column, Bunga can see all three trees.• On the third column, Bunga can see only the tree on the first row, as the…arrow_forwardComputer Science Please do a simple JAVA code for the Monty Hall problem. Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice? Please have the following Main allows the person playing to choose any door class door: should have data member methods Class person: should have data methodsarrow_forward
- 1. The entrance room (or the starting of the maze) is considered as level 1. Now, answer these following questions: (a). Write an algorithm to figure out how many maximum levels the maze can go up to. (b). Figure out the complexity of your algorithm. To create a maze some rooms of a building is connected. Starting room is called Entrance room. From the entrance room other rooms are there connected from it. However, some rooms of that maze- building have connected room from it, and some rooms do not have any connected room. Each of the room can have at most or up to two rooms connected from it. The starting room is the entrance room of the maze or building. Fore example: It can be any one like the followings: Exemple -: Room1 Roono Room Entrance Room Raom Room2 Room? Roo Roomo Here, maxinum level =7 Example -2; Entrace Room D- Room5 Room 2 Room 4 Maxximum level=3arrow_forwardWrite an algorithm to print all ways of arranging eight queens on an 8x8 chess board so that none of them share the same row, column, or diagonal. In this case, "diagonal" means all diagonals, not just the two that bisect the board.arrow_forwardThere are m towns in a straight line, with a road joining each pair of consecutive towns. Legends say that an ordinary person in one of these towns will become a hero by completing a sequence of n quests. The first quest will be completed in their home town, but after each quest they may complete their next quest either in the same town or after moving to a neighbouring town.For example, if n = 5 and m = 4, a resident of town 2 may become a hero as follows:• begin in town 2 for quest 1,• then move to town 3 for quest 2,• stay in town 3 for quest 3,• return to town 2 for quest 4, and• move to town 1 for quest 5.Design an algorithm which runs in O(nm) time and finds the total number of waysto complete n quests.arrow_forward
- The Monty Hall game is a statistical problem: there is a TV show (like the Monty Hall show) that allows contestants to choose between three doors, A, B, and C. Behind one of these doors is a new car (the winning door), and behind the other two are goats (the losing doors). After the contestant makes a choice, the game show host shows a goat behind one of the doors NOT chosen. The contestant is then given a choice to either switch to the other, non-opened door, or stick with their original guess. The interesting part of this “game" is the statistics involved –a person has a 1/3 chance of originally picking a winning door. The other door – that which is not revealed to have a goat but also was not originally chosen – actually has a 2/3 chance of being a winning door. Therefore, it is in the contestant's best interest to switch doors. You will create a program that simulates the Monty Hall game, where the computer plays the role of the host. The program must have no outputs, but 1) Ask…arrow_forwardThe Monty Hall game is a statistical problem: there is a TV show (like the Monty Hall show) that allows contestants to choose between three doors, A, B, and C. Behind one of these doors is a new car (the winning door), and behind the other two are goats (the losing doors). After the contestant makes a choice, the game show host shows a goat behind one of the doors NOT chosen. The contestant is then given a choice to either switch to the other, non-opened door, or stick with their original guess. The interesting part of this “game" is the statistics involved-a person has a 1/3 chance of originally picking a winning door. The other door chosen – actually has a 2/3 chance of being a winning door. Therefore, it is in the contestant's best interest to switch doors. that which is not revealed to have a goat but also was not originally You will create a program that simulates the Monty Hall game, where the computer plays the role of the host. The program must have no outputs, but 1) Ask the…arrow_forwardThe Knapsack Problem is a famous computer science problem that is defined as follows: imagine you are carrying a knapsack with capacity to hold a total of weight C. You are selecting among n items with values A={a_1, a_2, ... , a_n} and associated weights W={w_1, w_2, ... , w_n}. Here the weights and values are all positive (but not necessarily unique). You wish to maximize the total value of the items you select not exceeding the given weight capacity, i.e. maximize sum_{a in A} such that sum_{w in W} <= C. Please note that you can only select your items once. a) We can reformulate this as a 2D bottom-up dynamic programming problem as follows. Define T_{i,j} as the highest possible value sum considering items 1 through i and total weight capacity j (j <= C). What is the base case i.e. T_{0,j} for all j and T_{i,0} for all i?, and What is the loop statement?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning
C++ Programming: From Problem Analysis to Program...
Computer Science
ISBN:9781337102087
Author:D. S. Malik
Publisher:Cengage Learning
Binary Numbers and Base Systems as Fast as Possible; Author: Techquikie;https://www.youtube.com/watch?v=LpuPe81bc2w;License: Standard YouTube License, CC-BY
Binary Number System; Author: Neso Academy;https://www.youtube.com/watch?v=w7ZLvYAi6pY;License: Standard Youtube License