
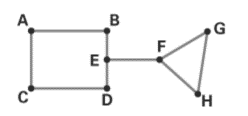
Use the preceding graph to answer the following questions:
a. How many edges does the graph have?
b. Which vertices are odd? Which are even?
c. Is the graph connected?
d. Does the graph have any bridges?
To find:
a. Find the number of edges in the graph.
b. Find the odd vertices and even vertices.
c. Check whether the graph is connected or not.
d. Check whether the graph has any bridge or not.
Answer to Problem 1CT
Solution:
a. The number of edges in the graph is 9.
b. The odd vertices are E, F and the even vertices are A, B, C, D, G, H.
c. The given graph is a connected graph.
d. The graph has one bridge namely EF.
Explanation of Solution
Graph:
A graph is a set of points, called vertices, and lines, called edges, that join pairs of vertices.
Vertex:
1. The points in the graph are called as vertex.
2. The point of intersection of a pair of edges is not a vertex.
3. A vertex of a graph is odd if it is the endpoint of an odd number of edges.
4. A vertex is even if it is the endpoint of an even number of edges.
Degree:
1. Degree of a vertex is the number of edges joined to that vertex.
2. If the degree is an odd number, then it is called as odd vertex.
3. If the degree of a vertex is even, then the vertex is called as even vertex.
Edge:
The line joining a pair of vertices is called as edge.
For example, we can refer a line joining the vertices A and B as edge AB or edge BA.
Connected graph:
A graph is connected if it is possible to travel from any vertex to any other vertex of the graph by moving along successive edges.
Bridge:
A bridge in a connected graph is an edge such that if it were removed, the graph would no longer be connected.
Calculation:
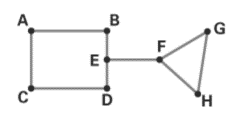
The graph in the problem is given below.
a. Find the number of edges:
The vertices in the graph are A, B, C, D, E, F, G and H.
The line joining the vertices is AB, AC, CD, BE, ED, EF, FG, FH and GH.
The number of edges in the graph is 9.
b. Find the odd vertices and even vertices:
Vertex A is the endpoint of two edges, so its degree is two.
Vertex B is the endpoint of two edges, so its degree is two.
Vertex C is the endpoint of two edges, so its degree is two.
Vertex D is the endpoint of two edges, so its degree is two.
Vertex E is the endpoint of two edges, so its degree is three
Vertex F is the endpoint of two edges, so its degree is three.
Vertex G is the endpoint of two edges, so its degree is two.
Vertex H is the endpoint of two edges, so its degree is two.
The odd vertices are E, F and the even vertices are A, B, C, D, G, H.
c. Check whether the graph is connected or not:
In a connected graph, there are no unreachable vertices.
In the given graph, we can travel from one vertex to another through successive edges.
For example, we can travel from vertex A to F through edges AB, BE, EF.
The given graph is a connected graph.
d. Check whether the graph has any bridge or not:
In the graph, if we remove the edge EF, then the graph becomes non connected graph. We cannot travel from vertex A to vertex G.
The edge EF is a bridge in the graph.
Want to see more full solutions like this?
Chapter 4 Solutions
MYLAB MATH WITH PEARSON ETEXT FOR MATHEM
- Answer number 1arrow_forwardUse a calculator to find a decimal approximation for the following trigonometric function. cot 226°54' cot 226°54' (Simplify your answer. Type an integer or a decimal. Round to eight decimal places as needed.)arrow_forwardIn preparing for the upcoming holiday season, Fresh Toy Company (FTC) designed a new doll called The Dougie that teaches children how to dance. The fixed cost to produce the doll is $100,000. The variable cost, which includes material, labor, and shipping costs, is $31 per doll. During the holiday selling season, FTC will sell the dolls for $39 each. If FTC overproduces the dolls, the excess dolls will be sold in January through a distributor who has agreed to pay FTC $10 per doll. Demand for new toys during the holiday selling season is extremely uncertain. Forecasts are for expected sales of 60,000 dolls with a standard deviation of 15,000. The normal probability distribution is assumed to be a good description of the demand. FTC has tentatively decided to produce 60,000 units (the same as average demand), but it wants to conduct an analysis regarding this production quantity before finalizing the decision. (a) Determine the equation for computing FTC's profit for given values of the…arrow_forward
- For all integers a and b, (a + b)^3 ≡ a^3 + b^3 (mod 3).arrow_forwardFind a plane containing the point (3, -3, 1) and the line of intersection of the planes 2x + 3y - 3z = 14 and -3x - y + z = −21. The equation of the plane is:arrow_forwardDetermine whether the lines L₁ : F(t) = (−2, 3, −1)t + (0,2,-3) and L2 : ƒ(s) = (2, −3, 1)s + (−10, 17, -8) intersect. If they do, find the point of intersection. ● They intersect at the point They are skew lines They are parallel or equalarrow_forward
- Answer number 15arrow_forwardWhy researchers are interested in describing measures of the center and measures of variation of a data set?arrow_forwardLet Χ be a real-valued character (mod k). Let k S = Σnx(n). n=1 If (a, k) = 1, ax(a)S = S (mod k). (iii) Write k = 2ºq where q is odd. Show that there is an integer a with (a, k) = 1 such that a = 3 (mod 2ª) and a = 2 (mod q). Deduce that 12S = 0 (mod k).arrow_forward
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL




