
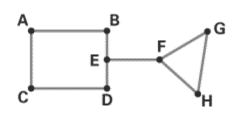
Use the preceding graph to answer the following questions:
a. How many edges does the graph have?
b. Which vertices are odd? Which are even?
c. Is the graph connected?
d. Does the graph have any bridges?
To find:
a. Find the number of edges in the graph.
b. Find the odd vertices and even vertices.
c. Check whether the graph is connected or not.
d. Check whether the graph has any bridge or not.
Answer to Problem 1CT
Solution:
a. The number of edges in the graph is 9.
b. The odd vertices are E, F and the even vertices are A, B, C, D, G, H.
c. The given graph is a connected graph.
d. The graph has one bridge namely EF.
Explanation of Solution
Graph:
A graph is a set of points, called vertices, and lines, called edges, that join pairs of vertices.
Vertex:
1. The points in the graph are called as vertex.
2. The point of intersection of a pair of edges is not a vertex.
3. A vertex of a graph is odd if it is the endpoint of an odd number of edges.
4. A vertex is even if it is the endpoint of an even number of edges.
Degree:
1. Degree of a vertex is the number of edges joined to that vertex.
2. If the degree is an odd number, then it is called as odd vertex.
3. If the degree of a vertex is even, then the vertex is called as even vertex.
Edge:
The line joining a pair of vertices is called as edge.
For example, we can refer a line joining the vertices A and B as edge AB or edge BA.
Connected graph:
A graph is connected if it is possible to travel from any vertex to any other vertex of the graph by moving along successive edges.
Bridge:
A bridge in a connected graph is an edge such that if it were removed, the graph would no longer be connected.
Calculation:
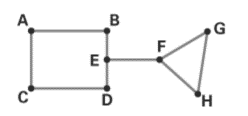
The graph in the problem is given below.
a. Find the number of edges:
The vertices in the graph are A, B, C, D, E, F, G and H.
The line joining the vertices is AB, AC, CD, BE, ED, EF, FG, FH and GH.
The number of edges in the graph is 9.
b. Find the odd vertices and even vertices:
Vertex A is the endpoint of two edges, so its degree is two.
Vertex B is the endpoint of two edges, so its degree is two.
Vertex C is the endpoint of two edges, so its degree is two.
Vertex D is the endpoint of two edges, so its degree is two.
Vertex E is the endpoint of two edges, so its degree is three
Vertex F is the endpoint of two edges, so its degree is three.
Vertex G is the endpoint of two edges, so its degree is two.
Vertex H is the endpoint of two edges, so its degree is two.
The odd vertices are E, F and the even vertices are A, B, C, D, G, H.
c. Check whether the graph is connected or not:
In a connected graph, there are no unreachable vertices.
In the given graph, we can travel from one vertex to another through successive edges.
For example, we can travel from vertex A to F through edges AB, BE, EF.
The given graph is a connected graph.
d. Check whether the graph has any bridge or not:
In the graph, if we remove the edge EF, then the graph becomes non connected graph. We cannot travel from vertex A to vertex G.
The edge EF is a bridge in the graph.
Want to see more full solutions like this?
Chapter 4 Solutions
Mathematics All Around, Books a la carte edition (6th Edition)
- Answer question 4 pleasearrow_forward16:39 < 文字 15:28 |美图秀秀 保存 59% 5G 46 照片 完成 Bonvicino - Period Name: 6. A right regular hexagonal pyramid with the top removed (as shown in Diagram 1) in such a manner that the top base is parallel to the base of the pyramid resulting in what is shown in Diagram 2. A wedge (from the center) is then removed from this solid as shown in Diagram 3. 30 Diogram 1 Diegrom 2. Diagram 3. If the height of the solid in Diagrams 2 and 3 is the height of the original pyramid, the radius of the base of the pyramid is 10 cm and each lateral edge of the solid in Diagram 3 is 12 cm, find the exact volume of the solid in Diagram 3, measured in cubic meters. Show all work. (T 文字 贴纸 消除笔 涂鸦笔 边框 马赛克 去美容arrow_forwardAnswer question 3 pleasearrow_forward
- Answer question 3 pleasearrow_forward38 Below triangle is isosceles. Find the value of x. 70° 60° x 20° Warrow_forwardProblem 11 (a) A tank is discharging water through an orifice at a depth of T meter below the surface of the water whose area is A m². The following are the values of a for the corresponding values of A: A 1.257 1.390 x 1.50 1.65 1.520 1.650 1.809 1.962 2.123 2.295 2.462|2.650 1.80 1.95 2.10 2.25 2.40 2.55 2.70 2.85 Using the formula -3.0 (0.018)T = dx. calculate T, the time in seconds for the level of the water to drop from 3.0 m to 1.5 m above the orifice. (b) The velocity of a train which starts from rest is given by the fol- lowing table, the time being reckoned in minutes from the start and the speed in km/hour: | † (minutes) |2|4 6 8 10 12 14 16 18 20 v (km/hr) 16 28.8 40 46.4 51.2 32.0 17.6 8 3.2 0 Estimate approximately the total distance ran in 20 minutes.arrow_forward
- - Let n = 7, let p = 23 and let S be the set of least positive residues mod p of the first (p − 1)/2 multiple of n, i.e. n mod p, 2n mod p, ..., p-1 2 -n mod p. Let T be the subset of S consisting of those residues which exceed p/2. Find the set T, and hence compute the Legendre symbol (7|23). 23 32 how come? The first 11 multiples of 7 reduced mod 23 are 7, 14, 21, 5, 12, 19, 3, 10, 17, 1, 8. The set T is the subset of these residues exceeding So T = {12, 14, 17, 19, 21}. By Gauss' lemma (Apostol Theorem 9.6), (7|23) = (−1)|T| = (−1)5 = −1.arrow_forwardLet n = 7, let p = 23 and let S be the set of least positive residues mod p of the first (p-1)/2 multiple of n, i.e. n mod p, 2n mod p, ..., 2 p-1 -n mod p. Let T be the subset of S consisting of those residues which exceed p/2. Find the set T, and hence compute the Legendre symbol (7|23). The first 11 multiples of 7 reduced mod 23 are 7, 14, 21, 5, 12, 19, 3, 10, 17, 1, 8. 23 The set T is the subset of these residues exceeding 2° So T = {12, 14, 17, 19, 21}. By Gauss' lemma (Apostol Theorem 9.6), (7|23) = (−1)|T| = (−1)5 = −1. how come?arrow_forwardShading a Venn diagram with 3 sets: Unions, intersections, and... The Venn diagram shows sets A, B, C, and the universal set U. Shade (CUA)' n B on the Venn diagram. U Explanation Check A- B Q Search 田arrow_forward
- 3. A different 7-Eleven has a bank of slurpee fountain heads. Their available flavors are as follows: Mountain Dew, Mountain Dew Code Red, Grape, Pepsi and Mountain Dew Livewire. You fill five different cups full with each type of flavor. How many different ways can you arrange the cups in a line if exactly two Mountain Dew flavors are next to each other? 3.2.1arrow_forwardBusinessarrow_forwardWhat is the area of this figure? 5 mm 4 mm 3 mm square millimeters 11 mm Submit 8 mm Work it out 9 mmarrow_forward
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL




