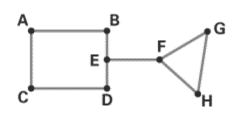
Use the preceding graph to answer the following questions: a. How many edges does the graph have? b. Which vertices are odd? Which are even? c. Is the graph connected? d. Does the graph have any bridges?

Question

Want to see more full solutions like this?

Answer 1

Textbook Question

Chapter 4.CT, Problem 1CT

Chapter 4.CT, Problem 1CT, Use the preceding graph to answer the following questions: a.How many edges does the graph have?

Use the preceding graph to answer the following questions:

a. How many edges does the graph have?

b. Which vertices are odd? Which are even?

c. Is the graph connected?

d. Does the graph have any bridges?

Expert Solution & Answer

To determine

To find:

a. Find the number of edges in the graph.

b. Find the odd vertices and even vertices.

c. Check whether the graph is connected or not.

d. Check whether the graph has any bridge or not.

Answer to Problem 1CT

Solution:

a. The number of edges in the graph is 9.

b. The odd vertices are E, F and the even vertices are A, B, C, D, G, H.

c. The given graph is a connected graph.

d. The graph has one bridge namely EF.

Explanation of Solution

Graph:

A graph is a set of points, called vertices, and lines, called edges, that join pairs of vertices.

Vertex:

1. The points in the graph are called as vertex.

2. The point of intersection of a pair of edges is not a vertex.

3. A vertex of a graph is odd if it is the endpoint of an odd number of edges.

4. A vertex is even if it is the endpoint of an even number of edges.

Degree:

1. Degree of a vertex is the number of edges joined to that vertex.

2. If the degree is an odd number, then it is called as odd vertex.

3. If the degree of a vertex is even, then the vertex is called as even vertex.

Edge:

The line joining a pair of vertices is called as edge.

For example, we can refer a line joining the vertices A and B as edge AB or edge BA.

Connected graph:

A graph is connected if it is possible to travel from any vertex to any other vertex of the graph by moving along successive edges.

Bridge:

A bridge in a connected graph is an edge such that if it were removed, the graph would no longer be connected.

Calculation:

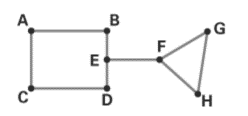
The graph in the problem is given below.

Mathematics All Around-Workbook, Chapter 4.CT, Problem 1CT

a. Find the number of edges:

The vertices in the graph are A, B, C, D, E, F, G and H.

The line joining the vertices is AB, AC, CD, BE, ED, EF, FG, FH and GH.

The number of edges in the graph is 9.

b. Find the odd vertices and even vertices:

Vertex A is the endpoint of two edges, so its degree is two.

Vertex B is the endpoint of two edges, so its degree is two.

Vertex C is the endpoint of two edges, so its degree is two.

Vertex D is the endpoint of two edges, so its degree is two.

Vertex E is the endpoint of two edges, so its degree is three

Vertex F is the endpoint of two edges, so its degree is three.

Vertex G is the endpoint of two edges, so its degree is two.

Vertex H is the endpoint of two edges, so its degree is two.

The odd vertices are E, F and the even vertices are A, B, C, D, G, H.

c. Check whether the graph is connected or not:

In a connected graph, there are no unreachable vertices.

In the given graph, we can travel from one vertex to another through successive edges.

For example, we can travel from vertex A to F through edges AB, BE, EF.

The given graph is a connected graph.

d. Check whether the graph has any bridge or not:

In the graph, if we remove the edge EF, then the graph becomes non connected graph. We cannot travel from vertex A to vertex G.

The edge EF is a bridge in the graph.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Students have asked these similar questions

Find mSW

توليد تمرين شامل حول الانحدار الخطي المتعدد بطريقة المربعات الصغرى

Which of the following is the general solution to y′′ + 4y = e^2t + 12 sin(2t) ?A. y(t) = c1 cos(2t) + c2 sin(2t) + 1/8 e^2t − 3t cos(2t)B. y(t) = c1e^2t + c2e^−2t + 1/4 te^2t − 3t cos(2t)C. y(t) = c1 + c2e^−4t + 1/12 te^2t − 3t cos(2t)D. y(t) = c1 cos(2t) + c2 sin(2t) + 1/8 e^2t + 3 sin(2t)E. None of the above. Please include all steps! Thank you!

Answer 2