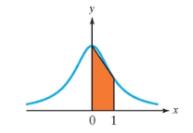
Problem 1SP: Find the exact values or state that the expression is undefined. a. sin122 b. arcsin1 c. sin13 Problem 2SP: Find the exact values. a. cos11 b. tan133 c. arctan0 Problem 3SP: Use a calculator to approximate the function values in both radians and degrees. a. tan17.92 b.... Problem 4SP: Use a calculator to approximate the degree measure (to 1 decimal place) or radian measure (to 4... Problem 5SP: Find the exact values. a. coscos11 b. cos1cos43 Problem 6SP: Find the exact value of sintan1125 . Problem 7SP: Find the exact value of cossin1211 . Problem 8SP: Write the expressiontansin1xx2+9 as an algebraic expression for x0 . Problem 9SP: For the construction of a house, a 16-ft by 6-ft wooden frame is made. Find the angle that the... Problem 10SP: Approximate each expression in radians, rounded to 4 decimal places. a. sec14 b. cos1512 Problem 1PE: A function must be on its entire domain to have an inverse function. Problem 2PE: If 23,12 is on the graph of y=cosx , what is the related point on y=cos1x ? Problem 3PE: The graph of y=tan1x has two (horizontal/vertical) asymptotes represented by the equations and . Problem 4PE: The domain of y=arctanx is . The output is a real number (or angle in radians) between and . Problem 5PE: In interval notation, the domain of y=cos1x is . The output is a real number (or angle in radians)... Problem 6PE: In interval notation, the domain ofy=sin1x is . The output is a real number (or angle in radians)... Problem 7PE: For Exercises 7-12, find the exact value or state that the expression is undefined. (See Example 1)... Problem 8PE: For Exercises 7-12, find the exact value or state that the expression is undefined. (See Example 1)... Problem 9PE: For Exercises 7-12, find the exact value or state that the expression is undefined. (See Example 1)... Problem 10PE: For Exercises 7-12, find the exact value or state that the expression is undefined. (See Example 1)... Problem 11PE: For Exercises 7-12, find the exact value or state that the expression is undefined. (See Example 1)... Problem 12PE: For Exercises 7-12, find the exact value or state that the expression is undefined. (See Example 1)... Problem 13PE: For Exercises 13-16, find the exact value. sin132+sin112 Problem 14PE: For Exercises 13-16, find the exact value. sin122sin11 Problem 15PE: For Exercises 13-16, find the exact value. 2sin1223 Problem 16PE: For Exercises 13-16, find the exact value. 2+3sin132 Problem 17PE: For Exercises 17-28, find the exact value or state that the expression is undefined. (See Example 2)... Problem 18PE: For Exercises 17-28, find the exact value or state that the expression is undefined. (See Example 2)... Problem 19PE: For Exercises 17-28, find the exact value or state that the expression is undefined. (See Example 2)... Problem 20PE Problem 21PE: For Exercises 17-28, find the exact value or state that the expression is undefined. (See Example 2)... Problem 22PE: For Exercises 17-28, find the exact value or state that the expression is undefined. (See Example 2)... Problem 23PE: For Exercises 17-28, find the exact value or state that the expression is undefined. (See Example 2)... Problem 24PE: For Exercises 17-28, find the exact value or state that the expression is undefined. (See Example 2)... Problem 25PE Problem 26PE: For Exercises 17-28, find the exact value or state that the expression is undefined. (See Example 2)... Problem 27PE Problem 28PE Problem 29PE: For Exercises 29-32, find the exact value. 3tan11+tan13 Problem 30PE: For Exercises 29-32, find the exact value. cos122+cos112 Problem 31PE: For Exercises 29-32, find the exact value. 2cos132tan133 Problem 32PE: For Exercises 29-32, find the exact value. 3tan11+cos122 Problem 33PE: For Exercises 33-36, use a calculator to approximate the function values in both radians and... Problem 34PE: For Exercises 33-36, use a calculator to approximate the function values in both radians and... Problem 35PE Problem 36PE Problem 37PE: For Exercises 37-46, use a calculator to approximate the degree measure (to 1 decimal place) or... Problem 38PE: For Exercises 37-46, use a calculator to approximate the degree measure (to 1 decimal place) or... Problem 39PE: For Exercises 37-46, use a calculator to approximate the degree measure (to 1 decimal place) or... Problem 40PE: For Exercises 37-46, use a calculator to approximate the degree measure (to 1 decimal place) or... Problem 41PE: For Exercises 37-46, use a calculator to approximate the degree measure (to 1 decimal place) or... Problem 42PE: For Exercises 37-46, use a calculator to approximate the degree measure (to 1 decimal place) or... Problem 43PE Problem 44PE: For Exercises 37-46, use a calculator to approximate the degree measure (to 1 decimal place) or... Problem 45PE Problem 46PE: For Exercises 37-46, use a calculator to approximate the degree measure (to 1 decimal place) or... Problem 47PE: For Exercises 47-58, find the exact values. (See Example 5) sinsin122 Problem 48PE: For Exercises 47-58, find the exact values. (See Example 5) arcsinsin53 Problem 49PE: For Exercises 47-58, find the exact values. (See Example 5) sin1sin54 Problem 50PE Problem 51PE: For Exercises 47-58, find the exact values. (See Example 5) coscos123 Problem 52PE: For Exercises 47-58, find the exact values. (See Example 5) arccoscos116 Problem 53PE: For Exercises 47-58, find the exact values. (See Example 5) cos1cos43 Problem 54PE: For Exercises 47-58, find the exact values. (See Example 5) coscos112 Problem 55PE: For Exercises 47-58, find the exact values. (See Example 5) tan1tan23 Problem 56PE: For Exercises 47-58, find the exact values. (See Example 5) tantan12 Problem 57PE Problem 58PE: For Exercises 47-58, find the exact values. (See Example 5) tan1tan6 Problem 59PE: For Exercises 59-70, find the exact values. (See Examples 6-7) costan133 Problem 60PE: For Exercises 59-70, find the exact values. (See Examples 6-7) sincos112 Problem 61PE Problem 62PE: For Exercises 59-70, find the exact values. (See Examples 6-7) sincos123 Problem 63PE: For Exercises 59-70, find the exact values. (See Examples 6-7) sincos134 Problem 64PE: For Exercises 59-70, find the exact values. (See Examples 6-7) sintan143 Problem 65PE: For Exercises 59-70, find the exact values. (See Examples 6-7) sintan11 Problem 66PE Problem 67PE: For Exercises 59-70, find the exact values. (See Examples 6-7) cossin127 Problem 68PE: For Exercises 59-70, find the exact values. (See Examples 6-7) costan1512 Problem 69PE: For Exercises 59-70, find the exact values. (See Examples 6-7) tancos156 Problem 70PE Problem 71PE: For Exercises 71-76, write the given expression as an algebraic expression. It is not necessary to... Problem 72PE: For Exercises 71-76, write the given expression as an algebraic expression. It is not necessary to... Problem 73PE: For Exercises 71-76, write the given expression as an algebraic expression. It is not necessary to... Problem 74PE: For Exercises 71-76, write the given expression as an algebraic expression. It is not necessary to... Problem 75PE Problem 76PE: For Exercises 71-76, write the given expression as an algebraic expression. It is not necessary to... Problem 77PE: To meet the requirements of the Americans with Disabilities Act (ADA) a wheelchair ramp must have a... Problem 78PE: A student measures the length of the shadow of the Washington Monument to be 620ft . If the... Problem 79PE: A balloon advertising an open house is stabilized by two cables of lengths 20ft and 40ft tethered to... Problem 80PE: A group of campers hikes down a steep path. One member of the group has an altimeter on his watch to... Problem 81PE: Navajo Tube Hill, a snow tubing hill in Utah, is 550ft long and has a 75-ft vertical drop. Find the... Problem 82PE: A ski run on Giant Steps Mountain in Utah is 1475m long. The difference in altitude from the... Problem 83PE Problem 84PE Problem 85PE: Show that sec1x=cos11x for x1 . Problem 86PE: Show that csc1x=sin11x for x1. Problem 87PE: Show that secx1+csc1x=2 for x1 . Problem 88PE Problem 89PE Problem 90PE: For Exercises 89-94, find the exact values. sec12 Problem 91PE Problem 92PE Problem 93PE: For Exercises 89-94, find the exact values. cot13 Problem 94PE: For Exercises 89-94, find the exact values. cot11 Problem 95PE: For Exercises 95-100, use a calculator to approximate each expression in radians, rounded to 4... Problem 96PE: For Exercises 95-100, use a calculator to approximate each expression in radians, rounded to 4... Problem 97PE: For Exercises 95-100, use a calculator to approximate each expression in radians, rounded to 4... Problem 98PE Problem 99PE: For Exercises 95-100, use a calculator to approximate each expression in radians, rounded to 4... Problem 100PE: For Exercises 95-100, use a calculator to approximate each expression in radians, rounded to 4... Problem 101PE: For Exercises 101-104, find the exact value if possible. Otherwise find an approximation to 4... Problem 102PE Problem 103PE: For Exercises 101-104, find the exact value if possible. Otherwise find an approximation to 4... Problem 104PE: For Exercises 101-104, find the exact value if possible. Otherwise find an approximation to 4... Problem 105PE Problem 106PE: For Exercises 105-108, find the inverse function and its domain and range. gx=6cosx4 for 0x Problem 107PE: For Exercises 105-108, find the inverse function and its domain and range. hx=4+tanx For 2x2 Problem 108PE: For Exercises 105-108, find the inverse function and its domain and range. kx=+sinx for 2x2 Problem 109PE: A video camera located at ground level follows the liftoff of an Atlas V Rocket from the Kennedy... Problem 110PE: The effective focal length f of a camera is the distance required for the lens to converge light to... Problem 111PE: For Exercises 111-114, use the relationship given in the right triangle and the inverse sine,... Problem 112PE: For Exercises 111-114, use the relationship given in the right triangle and the inverse sine,... Problem 113PE Problem 114PE: For Exercises 111-114, use the relationship given in the right triangle and the inverse sine,... Problem 115PE: For Exercises 115-120, find the exact solution to each equation. 2sin1x=0 Problem 116PE: For Exercises 115-120, find the exact solution to each equation. 3cos1x=0 Problem 117PE: For Exercises 115-120, find the exact solution to each equation. 6cos1x3=0 Problem 118PE Problem 119PE: For Exercises 115-120, find the exact solution to each equation. 4tan12x= Problem 120PE Problem 121PE Problem 122PE: Explain the flaw in the logic:cos4=22 . Therefore, cos122=4 . Problem 123PE Problem 124PE Problem 125PE: In calculus, we can show that the area below the graph of fx=11+x2 , above the x- axis, and between... Problem 126PE Problem 127PE: The vertical viewing angle to a movie screen is the angle formed from the bottom of the screen to a... Problem 128PE Problem 129PE: a. Graph the functions y=tan1x and y=xx33+x55 on the window 2,2,4 by 2,2,1 . b. Graph the... format_list_bulleted


 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell




