
Construct a mathematical model for each of the following problems. (The answers in the back of the book include both the mathematical model and the interpretation of its solution.) Use matrix
inverse methods to solve the model and then interpret the solution.
Concert tickets. A concert hall has
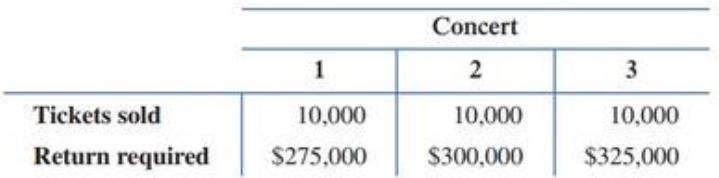
(A) How many tickets of each category should be sold to bring in each of the returns indicated in the table?
(B) Is it possible to bring in a return of
(C) Describe all the possible returns.
Want to see the full answer?
Check out a sample textbook solution
Chapter 4 Solutions
FINITE MATH.F/BUS,ECON,LIFE..-ACCESS
Additional Math Textbook Solutions
Pre-Algebra Student Edition
Intro Stats, Books a la Carte Edition (5th Edition)
Elementary Statistics
Algebra and Trigonometry (6th Edition)
College Algebra with Modeling & Visualization (5th Edition)
- Price (S) The graph below depicts a firm with market power. In the graph, MC represents the firm's marginal costs, ATC represents the average total costs, D represents demand, and MR represents marginal revenue. 110 70 60 50 40 30 20 MC ATC D 0 40 50 70 80 95 Quantity/Units MR a. At 60 units of output, how much would this profit-maximizing monopolist charge? b. How many units would it produce to maximize total revenue rather than total profit? c. What is the maximum quantity this firm can produce without incurring economic losses? d. Calculate the firm's profit at the profit-maximizing output and price. e. Why is this firm's marginal revenue curve below its demand curve? Explain.arrow_forwardA well-known company predominantly makes flat pack furniture for students. Variability with the automated machinery means the wood components are cut with a standard deviation in length of 0.45 mm. After they are cut the components are measured. If their length is more than 1.2 mm from the required length, the components are rejected. a) Calculate the percentage of components that get rejected. b) In a manufacturing run of 1000 units, how many are expected to be rejected? c) The company wishes to install more accurate equipment in order to reduce the rejection rate by one-half, using the same ±1.2mm rejection criterion. Calculate the maximum acceptable standard deviation of the new process.arrow_forwardFind the (exact) direction cosines and (rounded to 1 decimal place) direction angles of = (3,7,6)arrow_forward
- Forces of 9 pounds and 15 pounds act on each other with an angle of 72°. The magnitude of the resultant force The resultant force has an angle of pounds. * with the 9 pound force. The resultant force has an angle of with the 15 pound force. It is best to calculate each angle separately and check by seeing if they add to 72°.arrow_forward1. Sketch the following sets and determine which are domains: (a) |z−2+i| ≤ 1; - (c) Imz> 1; (e) 0≤ arg z≤ л/4 (z ± 0); Ans. (b), (c) are domains. (b) |2z+3| > 4; (d) Im z = 1; - (f) | z − 4| ≥ |z.arrow_forward8. Suppose that the moments of the random variable X are constant, that is, suppose that EX" =c for all n ≥ 1, for some constant c. Find the distribution of X.arrow_forward
- 9. The concentration function of a random variable X is defined as Qx(h) = sup P(x ≤ X ≤x+h), h>0. Show that, if X and Y are independent random variables, then Qx+y (h) min{Qx(h). Qr (h)).arrow_forward= Let (6,2,-5) and = (5,4, -6). Compute the following: บี.บี. บี. นี = 2 −4(u. v) = (-4). v= ū. (-40) (ū. v) v =arrow_forwardLet ā-6+4j- 1k and b = 7i8j+3k. Find a. b.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning  College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell





