Chapter 4.5, Problem 20E

To determine

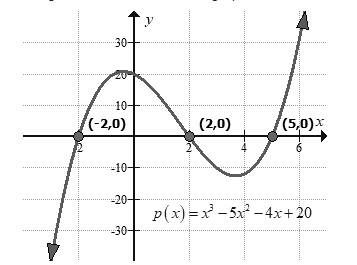
To find: the zeros of the given function. Also sketch the graph of the function.

Answer to Problem 20E

The zeros of the given function is $x=5,x=2$ and $x=-2$ .

Explanation of Solution

Given information:

A function is given as

  $p\left(x\right)=x^3-5x^2-4x+20$

Concept used:

Leading coefficient of a polynomial function is the coefficient of the leading term.

Degree of the polynomial is the degree of leading term or the height degree in the polynomial function.

For the polynomial $f\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+\mathrm{...}+a_{1}x+a_0$ the leading coefficient is $a_n$ and the degree is $n$ .

The end behavior can describe the graph of a polynomial function as  $x$  approaches $+\infty$ or as  $x$  approaches $-\infty$ .

The end behavior of a polynomial function can be determined by the leading coefficient and the degree of the polynomial.

If degree is even and leading coefficient is negative.

  $f\left(x\right)\to -\infty$ as $x\to -\infty$ and $f\left(x\right)\to -\infty$ as $x\to +\infty$ .

If degree is odd and leading coefficient is negative.

  $f\left(x\right)\to \infty$ as $x\to -\infty$ and $f\left(x\right)\to -\infty$ as $x\to +\infty$ .

If degree is odd and leading coefficient is positive.

  $f\left(x\right)\to -\infty$ as $x\to -\infty$ and $f\left(x\right)\to \infty$ as $x\to +\infty$ .

If degree is even and leading coefficient is positive.

  $f\left(x\right)\to \infty$ as $x\to -\infty$ and $f\left(x\right)\to \infty$ as $x\to +\infty$ .

Zeros of a polynomial function can be found by equating the function with 0.

Calculation:

Consider the given function.

  $p\left(x\right)=x^3-5x^2-4x+20$

Now, for zeros of the function equate the function with 0.

  $\begin{array}{l}p\left(x\right)=0\\ x^3-5x^2-4x+20=0\end{array}$

Now, factorize left side of $x^3-5x^2-4x+20=0$ as shown:

  $\begin{array}{c}{x}^3-5x^2-4x+20=0\\ x^2\left(x-5\right)-4\left(x-5\right)=0\\ \left(x-5\right)\left(x^2-4\right)=0\end{array}$

Solution can be found by equating each factor with 0.

  $\begin{array}{c}x-5=0\\ x=5\end{array}$

And

  $\begin{array}{c}{x}^2-4=0\\ x^2=4\\ x=\pm 2\end{array}$

Therefore, the zeros of the given function is $x=5,x=2$ and $x=-2$ ..

So, the graph crosses $x$ axis at $x=5,x=2,x=-2$ .

Degree is odd and leading coefficient is positive.

  $p\left(x\right)\to \infty$ as $x\to -\infty$ and $p\left(x\right)\to \infty$ as $x\to +\infty$ .

Graph:

The graph of the function can be sketched by the characteristics.