
Concept explainers
a.
Find
a.
Answer to Problem 106E
Explanation of Solution
Given information:
The figure shows point
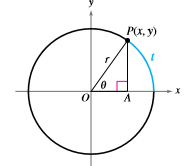
Find
Calculation:
Let us consider the following figure Also let this is a unit circle with radius
Hence, from the unit circle definitions of sine and cosine,
b.
What is the value of
b.
Answer to Problem 106E
Explanation of Solution
Given information:
The figure shows point
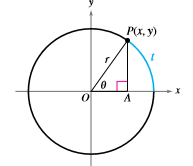
What is the value of
Calculation:
Let us consider the following figure Also let this is a unit circle with radius
The value of
Hence, we get
c.
Find
c.
Answer to Problem 106E
Explanation of Solution
Given information:
The figure shows point
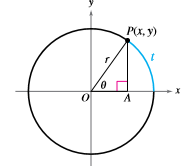
Use the definitions of sine and cosine given in this section to find
Calculation:
Let us consider the following figure Also let this is a unit circle with radius
Using the definition of sine and cosine,
As,
d.
what can you conclude from the part (a) and (c).
d.
Answer to Problem 106E
Explanation of Solution
Given information:
The figure shows point
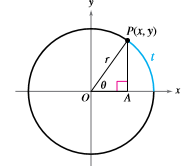
Based on your answers to parts (a) and (c), what can you conclude?
Calculation:
Let us consider the following figure Also let this is a unit circle with radius
From the answers in part (a) and (b), we can conclude that the value of trigonometric functions from unit circle definitions is equal to the value of trigonometric functions from rectangular co-ordinate definitions.
Hence, the trigonometric functions from unit circle is equal to the trigonometric functions from rectangular co-ordinate.
Chapter 4 Solutions
EBK PRECALCULUS W/LIMITS
- H.w WI M Wz A Sindax Sind dy max Утах at 0.75m from A w=6KN/M L=2 W2=9 KN/m P= 10 KN B Make the solution handwritten and not artificial intelligence because I will give a bad rating if you solve it with artificial intelligencearrow_forwardSolve by DrWz WI P L B dy Sind Ⓡ de max ⑦Ymax dx Solve by Dr ③Yat 0.75m from A w=6KN/M L=2 W2=9 kN/m P= 10 KN Solve By Drarrow_forwardHow to find the radius of convergence for the series in the image below? I'm stuck on how to isolate the x in the interval of convergence.arrow_forward
- Determine the exact signed area between the curve g(x): x-axis on the interval [0,1]. = tan2/5 secx dx andarrow_forwardSet up the partial fraction expansion of the function below. Do not explicitly solve for the variables 5 x²(x − 2)(x − 3)³ (24 - 81)² -arrow_forwardEvaluate the integral below: (4w (4w8) sec(4w) tan(4w) dwarrow_forward
- solve these pleasearrow_forwardA factorization A = PDP 1 is not unique. For A= 7 2 -4 1 1 1 5 0 2 1 one factorization is P = D= and P-1 30 = Use this information with D₁ = to find a matrix P₁ such that - -1 -2 0 3 1 - - 1 05 A-P,D,P P1 (Type an integer or simplified fraction for each matrix element.)arrow_forwardMatrix A is factored in the form PDP 1. Use the Diagonalization Theorem to find the eigenvalues of A and a basis for each eigenspace. 30 -1 - 1 0 -1 400 0 0 1 A= 3 4 3 0 1 3 040 3 1 3 0 0 4 1 0 0 003 -1 0 -1 Select the correct choice below and fill in the answer boxes to complete your choice. (Use a comma to separate vectors as needed.) A basis for the corresponding eigenspace is { A. There is one distinct eigenvalue, λ = B. In ascending order, the two distinct eigenvalues are λ₁ ... = and 2 = Bases for the corresponding eigenspaces are { and ( ), respectively. C. In ascending order, the three distinct eigenvalues are λ₁ = = 12/2 = and 3 = Bases for the corresponding eigenspaces are {}, }, and { respectively.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





