
Concept explainers
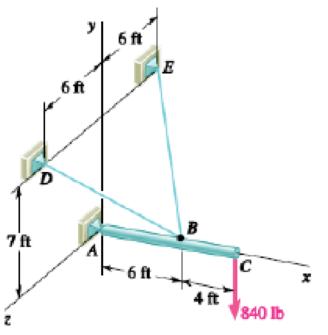
PROBLEM 4.105
A 10-ft boom is acted upon by the 840-lb force shown. Determine the tension in each cable and the reaction at the ball-and-socket joint at A.
The tension in each cable and the reaction at the ball and socket joint at A.
Answer to Problem 4.105P
The tension in cable BD is
Explanation of Solution
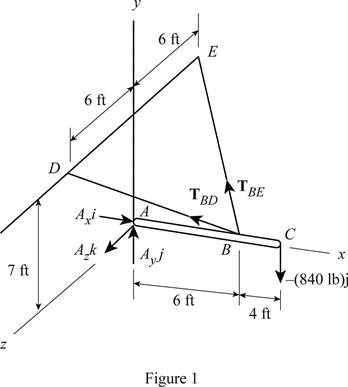
The free body diagram corresponding to the system of cable is shown in figure 1 plotted below.
A down ward force of magnitude
Write the equation to find the position vector
Here,
Write the equation to find the position vector
Here,
Write the equation to find the magnitude of
Here,
Write the equation to find the magnitude of
Here,
Write the equation to find the tension along cable BD.
Here,
Write the equation to find the tension along cable BE.
Here,
Write the equation to find the moments at point B due to force at D.
Here,
Write the equation to find the moment at point B due to force at point E.
Here,
Write the equation to find the moment of force at point B due to force at point C.
Here,
Write the equation to find the sum of moment of force at point B.
Here,
Substitute equation (VII), (VIII), and (IX) in equation (X) to find the
Substitute
Since sum of all external force acting on a body is zero, equate the equation for moments to zero.
Write the equation to find the sum of x components of force.
Write the equation to find the sum of y components of force.
Write the equation to find the sum of z component of forces.
Conclusion:
Substitute
Substitute
Substitute
Substitute
Substitute
Equate the coefficients of unit vectors
Equate the coefficient of unit vector
Equate the coefficients of unit vector
Substitute
Substitute
Substitute
Therefore, the tension in cable BD is
Want to see more full solutions like this?
Chapter 4 Solutions
Loose Leaf for Vector Mechanics for Engineers: Statics and Dynamics
- 4.110 A 7-ft boom is held by a ball and socket at A and by two cables EBF and DC; cable EBF passes around a frictionless pulley at B. Determine the tension in each cable.arrow_forwardAnswer the given problem. Show your complete solution. Provide a handwritten calculationarrow_forwardShow your complete and detailed solution.arrow_forward
- A 48-in. boom is held by a ball-and-socket joint at C and by two cables BF and DAF passes around a frictionless pulley at A . For the loading shown, determine the tension in each cable and the reaction at C.arrow_forwardThe rectangular plate shown weighs 93 lb and is held in the position shown by hinges at A and B and by cable EF. Assuming that the hinge at B does not exert any axial thrust and no couples exerted on both A and B, determine (a) the tension in the cable, (b) the reactions at A and B. y Solution: 12 in. 30 in. H 4 in. E 8 in. B 4 in. 25 in. 20 in. Xarrow_forwardA uniform circular rod with a weight of 8 lb and radius of 10 in. is attached to a pin at C and to the cable AB . Determine (a) the tension in the cable, (b) the reaction at C.arrow_forward
- The press shown below is used to emboss a small metal plate at E. The press is composed of 3 members: handle ABC, link BD, and piston DE that are connected by pins at points A, B. and D. A vertical force of 250 N is applied at point C. Determine: (a) The vertical component of the force exerted on the plate at E and the reactions at pin A. (b) The mechanical advantage of the press. Draw all required FBD's and put units on your answers. A 200 mm 60° 19T 20° 400 mm 15⁰ C C Parrow_forward2Answer the given problem. Provide a handwritten calculation and use a given, required, solution format.arrow_forwardE 2. A force, P of magnitude 90 lb is applied to member ACE, which is supported by a frictionless pin at D and by cable ABE. Assume that the tension is the same in portions AB and BE of the cable. For the case of a = 3in. , determine: (a) the tension in the cable, and (b) the reaction at D. Ans: TABE = 117 lb, D = 129.8 lb 56.3° B D 12 in. -5 in- -7 in-arrow_forward
- The lid of a roof scuttle weighs 75 lb. It is hinged at corners A and B and maintained in the desired position by a rod CD pivoted at C . A pin at end D of the rod fits into one of several holes drilled in the edge of the lid. For a = 50°, determine (a) the magnitude of the force exerted by rod CD, (b) the reactions at the hinges. Assume that the hinge at B does not exert any axial thrust.arrow_forward3. Determine the tension in each wire that support the 75-kg homogeneous plate shown.arrow_forwardA thin ring of mass 2 kg and radius r=140 mm is held against a frictionless wall by a 125-mm string AB. Determine (a) the distance d, (b) the tension in the string, (c) the reaction at C.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





