Chapter 4.3, Problem 24E

Presidents and first ladies: The presents the ages of the last 10 U.S. presidents and their wives on the first day of their presidencies.

1. Compute the least-squares regression line for predicting the president’s age from the first lady’s age.
2. Compute the coefficient of determination-
3. Construct a scatterplot of the presidents' ages (y) versus the first ladies' ages (x).
4. Which point is an outlier?
5. Remove die outlier and compute the least-squares regression line for predicting the president’s age from the first lady: s age.
6. Is the outlier influential? Explain.
7. Compute the coefficient of determination for the data set with the outlier removed. Is due proportion of variation explained by due least-squares regression he greater, less. or about the same without due outlier? Explain.

To determine

To Calculate: The least-squares regression line for predicting the president’s age from lady’s age.

Answer to Problem 24E

The least-squares regression line is,

  $\widehat{y}=14+0.8426x$

Explanation of Solution

Given: The following table presents the age of the president’s and their wives on the first day of their presidencies.

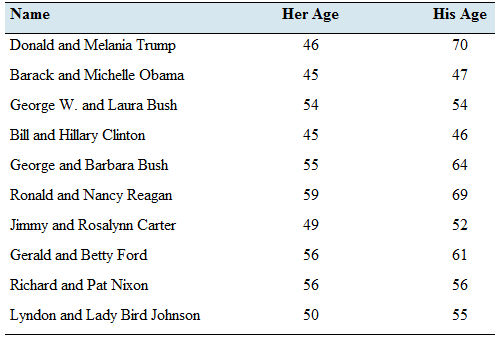
Name	Her Age	His Age
Donald and Melania Trump	46	70
Barak and Mechelle Obama	45	47
George W. and Laura Bush	54	54
Bill and Hillary Clinton	45	46
George and Babara Bush	55	64
Ronald and Nancy Reagan	59	69
Jimmy and Rosalyn Carter	49	52
Gerald and Betty Ford	56	61
Richard and Pat Nixon	56	56
Lyndon and Lady Bird Johnson	50	55

Calculation:

Here,

  $y$ = president’s age

  $x$ = lady’s age

From below formula we can find least regression line.

  $\widehat{y}=b_0+b_{1}x$

where $b_0$ and $b_1$ are constants.

We can find these constants from below formulas.

  $\begin{array}{l}{b}_1=r\frac{s_y}{s_x}\\ b_0=\overline{y}-b_1\overline{x}\\ r=\frac{1}{n-1}{\displaystyle \sum \left(\frac{x-\overline{x}}{s_x}\right)}\left(\frac{y-\overline{y}}{s_y}\right)\end{array}$

Where,

  $n$ is the number of observations

  $\overline{x}$ is the average of $x$

  $\overline{y}$ is the average of $y$

  $s_x$ is the standard deviation of $x$

  $s_y$ is the standard deviation of $y$

Descriptive Statistics
	N	Mean	Std. Deviation
His age	10	57.40	8.409
Her age	10	51.50	5.148
Valid N (listwise)	10

  $n=10$    number of observations

  $\overline{x}=51.5$    average of lady’s age $\left(x\right)$

  $\overline{y}=57.4$    average of president’s age $\left(y\right)$

  $s_x=5.148$    standard deviation of $x$

  $s_y=8.409$    standard deviation of $y$

  $r=0.5159$    correlation between $x$ and $y$

To find constants,

  $\begin{array}{l}{b}_1=r\frac{s_y}{s_x}\\ b_1=0.5159\times \frac{8.409}{5.148}\\ =0.8426\end{array}$

And,

  $\begin{array}{c}{b}_0=\overline{y}-b_1\overline{x}\\ =57.4-\left(0.8426\times 51.5\right)\\ b_0=14.0061\\ b_0\approx 14\end{array}$

By substituting above formula,

  $\begin{array}{c}y=b_0+b_{1}x\\ y=14+0.8426x\end{array}$

Conclusion:

The least-squares regression line for predicting the president’s age from lady’s age is,

  $y=14+0.8426x$

To determine

To find: The correlation coefficient of the two variables.

Answer to Problem 24E

The correlation coefficient is found to be,

  $r=0.5159$

Explanation of Solution

Calculation:

The correlation coefficient $\left(r\right)$ is given by the formula,

  $r=\frac{1}{n-1}{\displaystyle \sum \left(\frac{x-\overline{x}}{s_x}\right)\left(\frac{y-\overline{y}}{s_y}\right)}$

Where $s_x$ and $s_y$ is the standard deviation of $x$ and $y$ .

The means and the standard deviations of the both variables can be obtained by using the Excel.

Descriptive Statistics
	N	Mean	Std. Deviation
His age	10	57.40	8.409
Her age	10	51.50	5.148
Valid N (listwise)	10

Then,

  $\begin{array}{c}\overline{x}=51.5\\ s_x=5.148\\ \overline{y}=57.4\\ s_y=8.409\end{array}$

Then, a table should be constructed to calculate $r$ as follows.

  $\begin{array}{l}\begin{array}{ccccc}\begin{array}{c}\text{Her}\text{Age}\\ x\end{array}& \begin{array}{c}\text{His}\text{Age}\\ y\end{array}& \frac{x-\overline{x}}{s_x}& \frac{y-\overline{y}}{s_y}& \left(\frac{x-\overline{x}}{s_x}\right)\left(\frac{y-\overline{y}}{s_y}\right)\\ 46& 70& -1.0684& 1.4984& -1.6009\\ 45& 47& -1.2626& -1.2368& 1.5616\\ 54& 54& 0.4856& -0.4043& -0.1963\\ 45& 46& -1.2626& -1.3557& 1.7117\\ 55& 64& 0.6799& 0.7849& 0.5337\\ 59& 69& 1.4569& 1.3795& 2.0098\\ 49& 52& -0.4856& -0.6422& 0.3119\\ 56& 61& 0.8741& 0.4281& 0.3742\\ 56& 56& 0.8741& -0.1665& -0.1455\\ 50& 55& -0.2914& -0.2854& 0.0832\end{array}\\ {\displaystyle \sum \left(\frac{x-\overline{x}}{s_x}\right)\left(\frac{y-\overline{y}}{s_y}\right)}=4.6434\end{array}$

The correlation coefficient can be calculated as,

  $\begin{array}{c}r=\frac{1}{10-1}\times 4.6434\\ =\frac{4.6434}{9}\\ r=0.5159\end{array}$

Conclusion:

The correlation coefficient between the interest rates for two mortgage plans is found tobe,

  $r=0.5159$

To determine

To graph: The scatter plot of the given two quantitative variables.

Explanation of Solution

Graph:

Let $x$ be the lady’s age and $y$ be the president’s age. The scatter plot can be constructed by the ordered pairs using the Excel.

  

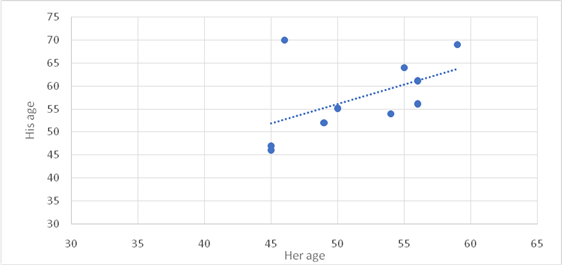
Interpretation:

Out of all these $10$ ordered pairs, there is a weak positive relationship between president’s age and lady’s age.

To determine

To Identify: The outliers within the given data.

Answer to Problem 24E

There is one outlier which is age $70$

Explanation of Solution

Explain:

Here, Excel is used to calculate below statistics.

  $Q_1$ is the middle value in the first half of the rank-ordered data set.

  $Q_2$ is the median value in the set.

  $Q_3$ is the middle value in the second half of the rank-ordered data set.

The interquartile range is equal to $Q_3$ minus $Q_1$ .

To calculate upper bound,

  $\begin{array}{c}{Q}_3+\left(IQR\times 1.5\right)=Q_3+\left(\left(Q_3-Q_1\right)\times 1.5\right)\\ =56.75+\left(56.75-48.5\right)\times 1.5\\ =56.75+8.25\times 1.5\\ =56.75+12.375\\ Q_3+\left(IQR\times 1.5\right)=69.125\end{array}$

To calculate lower bound,

  $\begin{array}{c}{Q}_1-\left(IQR\times 1.5\right)=Q_1-\left(\left(Q_3-Q_1\right)\times 1.5\right)\\ =48.5-\left(56.75-48.5\right)\times 1.5\\ =48.5-8.25\times 1.5\\ =48.5-12.375\\ Q_1-\left(IQR\times 1.5\right)=36.125\end{array}$

An outlier is a data point that lies outside the upper bound and lower bound.

  $\begin{array}{ccccc}{Q}_1& Q_3& IQR& \begin{array}{l}\text{Lower }\\ \text{Bound}\end{array}& \begin{array}{l}\text{Upper}\\ \text{Bound}\end{array}\\ 48.5& 56.75& 8.25& 36.125& 69.125\end{array}$

Out of all $10$ ordered pairs, only one value can be identified as an outlier, where the age is not between the lower bound and upper bound.

  $70>69.125$

To determine

To find: The least-squares regression line for predicting the president’s age from lady’s age with removing outlier.

Answer to Problem 24E

The least-squares regression is,

  $y=-14.7+1.3567x$

Explanation of Solution

Calculation:

Here,

  $y$ = president’s age

  $x$ = lady’s age

From below formula we can find least regression line.

  $\widehat{y}=b_0+b_{1}x$

where $b_0$ and $b_1$ are constants.

We can find constants from below formulas.

  $\begin{array}{l}{b}_1=r\frac{s_y}{s_x}\\ b_0=\overline{y}-b_1\overline{x}\\ r=\frac{1}{n-1}{\displaystyle \sum \left(\frac{x-\overline{x}}{s_x}\right)}\left(\frac{y-\overline{y}}{s_y}\right)\end{array}$

Where,

  $n$ is the number of observations$\overline{x}$ is the average of $x$

  $\overline{y}$ is the average of $y$

  $s_x$ is the standard deviation of $x$

  $s_y$ is the standard deviation of $y$

When the outlier is removed, the number of ordered pairs is $9$ .

Descriptive Statistics
	N	Mean	Std. Deviation
His age	9	56.00	7.583
Her age	9	52.11	5.061
Valid N (listwise)	9

  $n=9$   ; number of observations.

  $\overline{x}=52.11$  ; average of lady’s age $\left(x\right)$

  $\overline{y}=56$  ; average of president’s age $\left(y\right)$

  $s_x=5.061$  ; standard deviation of $x$

  $s_y=7.583$  ; standard deviation of $y$

  $r=0.9055$  ; correlation between $x$ and $y$

To find constants,

  $\begin{array}{l}{b}_1=r\frac{s_y}{s_x}\\ b_1=(0.9055)\frac{7.583}{5.061}\\ =1.3567\end{array}$

And,

  $\begin{array}{l}{b}_0=\overline{y}-b_1\overline{x}\\ =56-(1.3567)\times 52.11\\ =-14.6976\\ =-14.7\end{array}$

By substituting into the above formula,

  $\begin{array}{l}y=b_0+b_{1}x\\ y=-14.7+1.3567x\end{array}$

Conclusion:

The least-squares regression line for predicting the president’s age from lady’s age is,

  $y=-14.7+1.3567x$

To determine

To Check: The influence of outlier.

Answer to Problem 24E

Yes. It is influenced.

Explanation of Solution

Explain:

Descriptive Statistics
	N	Mean	Std. Deviation
His age	10	57.40	8.409
Her age	10	51.50	5.148
Valid N (listwise)	10
Descriptive Statistics
	N	Mean	Std. Deviation
His age	9	56.00	7.583
Her age	9	52.11	5.061
Valid N (listwise)	9

To calculate above statistics, Excel is used. Here we can see statistics with outlier and without outlier. Second table shows statistics without outlier. Total number of observations, mean and standard deviation of dependent and independent variables are changed. So, it influences to least squares regression line for predicting the president’s age from lady’s age.

To determine

To find: The correlation coefficient of the two variables without outlier.

Answer to Problem 24E

The correlation coefficient is found to be,

  $r=0.9055$

Explanation of Solution

Calculation:

The correlation coefficient $\left(r\right)$ is given by the formula,

  $r=\frac{1}{n-1}{\displaystyle \sum \left(\frac{x-\overline{x}}{s_x}\right)\left(\frac{y-\overline{y}}{s_y}\right)}$

Where $s_x$ and $s_y$ is the standard deviation of $x$ and $y$ .

The means and the standard deviations of the both variables can be obtained by using the Excel.

For the remaining $9$ pairs without the outlier,

Descriptive Statistics
	N	Mean	Std. Deviation
His age	9	56.00	7.583
Her age	9	52.11	5.061
Valid N (listwise)	9

Then,

  $\begin{array}{c}\overline{x}=52.11\\ s_x=5.061\\ \overline{y}=56\\ s_y=7.583\end{array}$

Then, a table should be constructed to calculate $r$ as follows.

  $\begin{array}{l}\begin{array}{ccccc}x& y& \frac{x-\overline{x}}{s_x}& \frac{y-\overline{y}}{s_y}& \left(\frac{x-\overline{x}}{s_x}\right)\left(\frac{y-\overline{y}}{s_y}\right)\\ 45& 47& -1.4051& -1.1869& 1.6677\\ 54& 54& 0.3732& -0.2637& -0.0984\\ 45& 46& -1.4051& -1.3187& 1.8529\\ 55& 64& 0.5708& 1.0550& 0.6022\\ 59& 69& 1.3612& 1.7144& 2.3336\\ 49& 52& -0.6147& -0.5275& 0.3243\\ 56& 61& 0.7684& 0.6594& 0.5067\\ 56& 56& 0.7684& 0& 0\\ 50& 55& -0.4171& -0.1319& 0.0550\end{array}\\ {\displaystyle \sum \left(\frac{x-\overline{x}}{s_x}\right)\left(\frac{y-\overline{y}}{s_y}\right)}=7.2438\end{array}$

The correlation coefficient can be calculated as,

  $\begin{array}{c}r=\frac{1}{9-1}\times 7.2438\\ =\frac{7.2438}{8}\\ r=0.9055\end{array}$

Conclusion:

The correlation coefficient between the interest rates for two mortgage plans is found to be,

  $r=0.9055$