Probability and Statistical Inference (9th Edition)
9th Edition
ISBN: 9780321923271
Author: Robert V. Hogg, Elliot Tanis, Dale Zimmerman
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 4.2, Problem 8E
A certain raw material is classified as to moisture content X (in percent) and impurity Y (in percent). Let X and Y have the joint pmf given by
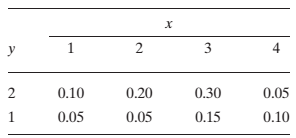
(a) Find the marginal pmfs, the
(b) Find the
(c) If additional heating is needed with high moisture content and additional filtering with high impurity such that the additional cost is given by the
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
6.54 Let Y₁, Y2,..., Y, be independent Poisson random variables with means 1, 2,..., An
respectively. Find the
a probability function of
Y.
b conditional probability function of Y₁, given that Y = m.
Y₁ = m.
c conditional probability function of Y₁+Y2, given that
6.55 Customers arrive at a department store checkout counter according to a Poisson distribution
with a mean of 7 per hour. In a given two-hour period, what is the probability that 20 or more
customers will arrive at the counter?
6.56 The length of time necessary to tune up a car is exponentially distributed with a mean of
.5 hour. If two cars are waiting for a tune-up and the service times are independent, what is
the probability that the total time for the two tune-ups will exceed 1.5 hours? [Hint: Recall the
result of Example 6.12.]
6.57 Let Y, Y2,..., Y,, be independent random variables such that each Y, has a gamma distribution
with parameters a, and B. That is, the distributions of the Y's might have different a's, but…
6.82
6.83
6.84
6.85
*6.86
6.87
If Y is a continuous random variable and m is the median of the distribution, then m is such
that P(Ym) = P(Y ≥ m) = 1/2. If Y₁, Y2,..., Y, are independent, exponentially dis-
tributed random variables with mean ẞ and median m, Example 6.17 implies that Y(n) =
max(Y₁, Y., Y) does not have an exponential distribution. Use the general form of FY() (y)
to show that P(Y(n) > m) = 1 - (.5)".
Refer to Exercise 6.82. If Y₁, Y2,..., Y,, is a random sample from any continuous distribution
with mean m, what is P(Y(n) > m)?
Refer to Exercise 6.26. The Weibull density function is given by
-my" m-le-y/a
f(y)= α
0.
y > 0,
elsewhere,
where a and m are positive constants. If a random sample of size n is taken from a Weibull
distributed population, find the distribution function and density function for Y(1) = min(Y1,
Y2,Y). Does Y(1) = have a Weibull distribution?
Let Y₁ and Y2 be independent and uniformly distributed over the interval (0, 1). Find
P(2Y(1) 0,
elsewhere,…
6.26
The Weibull density function is given by
e-y/a
f(y) = α
0.
y > 0,
elsewhere,
where a and m are positive constants. This density function is often used as a model for the
lengths of life of physical systems. Suppose Y has the Weibull density just given. Find
a the density function of UY".
b E(Y) for any positive integer k.
6.27
Let Y have an exponential distribution with mean ẞ.
6.28
6.29
a Prove that W = √Y has a Weibull density with α = ẞ and m = 2.
b
Use the result in Exercise 6.26(b) to give E(Yk/2) for any positive integer k.
Let Y have a uniform (0, 1) distribution. Show that U = -2ln(Y) has an exponential distri-
bution with mean 2.
The speed of a molecule in a uniform gas at equilibrium is a random variable V whose density
function is given by
6.30
6.31
6.32
f(v) = av²e-by², v > 0,
where b = m/2kT and k, T, and m denote Boltzmann's constant, the absolute temperature,
and the mass of the molecule, respectively.
a Derive the distribution of W = mV2/2, the kinetic energy of…
Chapter 4 Solutions
Probability and Statistical Inference (9th Edition)
Ch. 4.1 - For each of the following functions, determine the...Ch. 4.1 - Roll a pair of four-sided dice, one red and one...Ch. 4.1 - Let the joint pmf of X and Y be defined by...Ch. 4.1 - Select an (even) integer randomly from the set...Ch. 4.1 - Each part of Figure 4.1-5 depicts the sample space...Ch. 4.1 - The torque required to remove bolts in a steel...Ch. 4.1 - A particle starts at (0,0) and moves in one-unit...Ch. 4.1 - In a smoking survey among boys between the ages of...Ch. 4.1 - A manufactured item is classified as good, a...Ch. 4.2 - Prob. 1E
Ch. 4.2 - Prob. 2ECh. 4.2 - Roll a fair four-sided die twice. Let X equal the...Ch. 4.2 - Let X and Y have a trinomial distribution with...Ch. 4.2 - Prob. 5ECh. 4.2 - The joint pmf of X and Y is f(x,y)=16,0x+y2, where...Ch. 4.2 - Let the joint pmf of X and Y be...Ch. 4.2 - A certain raw material is classified as to...Ch. 4.2 - Prob. 9ECh. 4.2 - If the correlation coefficient exists, show that...Ch. 4.3 - Let X and Y have the joint pmf...Ch. 4.3 - Let the joint pmf f(x,y) of X and Y be given by...Ch. 4.3 - Let W equal the weight of laundry soap in a...Ch. 4.3 - The gene for eye color in a certain male fruit fly...Ch. 4.3 - Let X and Y have a trinomial distribution with...Ch. 4.3 - An insurance company sells both homeowners...Ch. 4.3 - Using the joint pmf from Exercise 4.2-3, find the...Ch. 4.3 - A fair six-sided die is rolled 30 independent...Ch. 4.3 - Let X and Y have a uniform distribution on the set...Ch. 4.3 - Let fX(x)=110,x=0,1,2,...,9, and...Ch. 4.3 - Suppose that X has a geometric distribution with...Ch. 4.5 - Let X and Y have a bivariate normal distribution...Ch. 4.5 - Show that the expression in the exponent of...Ch. 4.5 - Let X and Y have a bivariate normal distribution...Ch. 4.5 - Let X and Y have a bivariate normal...Ch. 4.5 - Let X denote the height in centimeters and Y the...Ch. 4.5 - For a freshman taking introductory statistics and...Ch. 4.5 - For a pair of gallinules, let X equal the weight...Ch. 4.5 - Let X and Y have a bivariate normal distribution...Ch. 4.5 - Let X and Y have a bivariate normal distribution....Ch. 4.5 - In a college health fitness program, let X denote...Ch. 4.5 - For a female freshman in a health fitness program,...Ch. 4.5 - Prob. 12ECh. 4.5 - An obstetrician does ultrasound examinations on...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, probability and related others by exploring similar questions and additional content below.Similar questions
- QIA Let F-4c24, countible or, A, countible), show that is o-algebra. B Let (Fne N) is family of a-algebra on 2, prove that F. o-algebra Q2: Prove that: 1. X, is martingale -esin 2. M, -e sin B,, is martingale by using Ito formula Q3: A Let X, has stochastic differential with drift p(x)=-bx + c, and diffusion o²(x)=4x, let Y√X,, where X, ≥0, find dr B: Let X, -(-s), Ito integral process, find dx, and [x.xko). Q4: Let Y, =[x,dB, is Ito integral, such that X, is nonrandom process, find: التوزيع 1. The distribution of Y 2. The moment generating function of Y,.arrow_forwardSolve the following Probability Problem (solve all parts) HW 2.x. (Headless Hunt)The Headless Hunt is an organization of 88 Hogwarts ghosts so elite thateven Nearly Headless Nick was annually denied admission for decades,despite being The Gryffindor ghost. The ghosts love playing sports anddecided to get together and have either a Head Polo tournament or aHorseback Head-Juggling tournament. However, even if they are ghosts,they still have jobs so some of them might have an urgent haunting as-signment. In order for no one to be left behind they need to be able tosplit into teams of equal numbers. Head polo teams consist of 4 playerswhereas Horseback Head-Juggling teams have 11 players. Assume thatany number of them from 1 to 88 show up with equal probability. a) What is the probability they will be able to play one of the twotournaments?b) If in addition to the previous 2 sports there was one more option, atournament in Headless bowling which is played in teams of 8 players,what would…arrow_forward42. Consider the following joint probability table. B₁ B2 B3 B4 A 0.09 0.22 0.15 0.20 A 0.03 0.10 0.09 0.12arrow_forward
- EXERCISES 4.3 Mechanics 41. Consider the following contingency table. B B A 26 34 Ac 14 26 a. Convert the contingency table into a joint probability table. b. What is the probability that A occurs? ن فة What is the probability that A and B occur? d. Given that B has occurred, what is the probability that A occurs? e. Given that A has occurred, what is the probability that B occurs? f. Are A and B mutually exclusive events? Explain. g. Are A and B independent events? Explain. 42. Consider the following joint probability table. B₁ B2 B3 BA A 0.09 0.22 0.15 0.20 Ac 0.03 0.10 0.09 0.12arrow_forwardCan u make a room for mearrow_forwardالتمرين الأول: 08) نقاط) نرمي رباعي وجوه مرقم من ا إلى 4 بحيث إحتمال وجوهه يحقق العلاقة التالية: - 24 = (3)P(1) = ) = 4P -1 أحسب احتمال كل وجه. -2 (١ أحسب احتمال الحادثة : الحصول على عدد زوجي). ب استنتج احتمال الحادثة ة. -3 أحسب احتمال الحادثة B الحصول على عدد د أكبر أو يساوي (2)arrow_forward
- Please solve the following Probability problem. Show all work and solve all parts that are asked: HW 1.y.(Yutnori) Yutnori is played by 2 (groups of) players on a gameboard with pieces thatmove around. Each player takes turns throwing yut sticks - each stick hastwo sides, round and flat, which makes the stick roll. Five combinationsare possible with yut sticks: do, gae, geol, yut and mo. A player achievinga yut or mo is allowed to roll again. Combinations and the number ofmoves they allow on the gameboard are presented in Figure 3 (flat sideup is blank and round side up is filled with x-es). Assuming each of the 4 Yut sticks falls on both of its sides with equalprobability, what is the probability that:a) you roll a yut?b) you roll a geol ?c) you get a second roll?d) you move 6 spaces in your first turn?In reality, a typical Yut stick is designed so that the probability of flat sidefacing up is around 60%. Try to think of what the previous probabilitieswould be in this case.arrow_forwardPlease solve the following Probability Problem, please show all work and solve what is asked: HW 1.w. (Special game)The atmosphere has heated up and a fight erupted! There are n + 1players and somebody threw the first punch. Once a person is punched,they punch another person in the group at random. What are the oddsthat after m iterations:a) Nobody punches the person who started it?b) Nobody gets punched twice?Now take it up a notch: imagine the first person punched N other peopleat random, and once someone gets punched, they punch another N peoplein the group at random, and so on. Again, what are the odds that afterm iterations:a) Nobody punches the person who started it?b) Nobody gets punched twice?arrow_forwardQ1. A chest of drawers has 3 drawers. Each drawer has 2 boxes. The boxes of one drawer contain a silver coin in each respectively, the boxes of another a gold coin in each box, and the boxes of the third drawer a gold and a silver coin, respectively. A drawer is selected at random and a box from the drawer is selected at random and opened. The coin is found to be silver. What is the probability that the coin in the other box is gold? (Harder Problem)arrow_forward
- Please solve the following Probability Problem: Show all work and complete what is askedarrow_forwardPlease solve the following probability problem. Show all work and must solve all parts HW 1.z. (Mingle)A number is called and players need to group up and enter rooms. Ifplayers do not manage to make it into the rooms in time, or if a room hasless or more players than it is supposed to have, they will be eliminated.Assume there are 200 people other than you and the number called is 10.Determine the probability that you will form the group of the correct sizein each of the following cases:a) Imagine you had no better strategy than going to each of the 200people and tossing a fair coin to determine if they will join yourgroup or not.b) Imagine everybody else is divided into 25 groups of 4 people and 20groups of 5 people. Among all the possible groups, you are choosingto join two at random.c) Imagine everybody else is divided into 20 groups of 4 people, 10groups of 2 people and 20 groups of 5 people. You are choosing tojoin two groups at random.d) Imagine everybody else is divided into 20…arrow_forwardAre the two statements A and B equivalent? (A) p~q (B) ~pq ☐ Statement A and B are equivalent. ☐ Statement A and B are not equivalent as their values in three rows are not identical. ☐ Statement A and B are not equivalent as their values in one row is not identical. ☐ Statement A and B are not equivalent as their values in two row are not identical.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Mod-01 Lec-01 Discrete probability distributions (Part 1); Author: nptelhrd;https://www.youtube.com/watch?v=6x1pL9Yov1k;License: Standard YouTube License, CC-BY
Discrete Probability Distributions; Author: Learn Something;https://www.youtube.com/watch?v=m9U4UelWLFs;License: Standard YouTube License, CC-BY
Probability Distribution Functions (PMF, PDF, CDF); Author: zedstatistics;https://www.youtube.com/watch?v=YXLVjCKVP7U;License: Standard YouTube License, CC-BY
Discrete Distributions: Binomial, Poisson and Hypergeometric | Statistics for Data Science; Author: Dr. Bharatendra Rai;https://www.youtube.com/watch?v=lHhyy4JMigg;License: Standard Youtube License