
Concept explainers
(a)
An expression for the probability that an electron in ground state will be found outside a sphere of radius
(a)
Answer to Problem 78AP
The expression for the probability that an electron in ground state will be found outside a sphere of radius
Explanation of Solution
Write the expression for the radial probability density function for the Hydrogen atom in ground state.
Here,
Write the expression to find the probability to for an electron in grounds state to be found outside a sphere of radius
The probability outside a sphere is to be found. So integration must be done from radius of sphere to infinity.
Use expression (I) in (III) to find
Integrate expression (IV) by integration by parts.
Simplify expression (V) to find
Conclusion:
Apply limits from
Therefore, the expression for the probability that an electron in ground state will be found outside a sphere of radius
(b)
Graph the relation between probability and
(b)
Answer to Problem 78AP
The graph between probability and
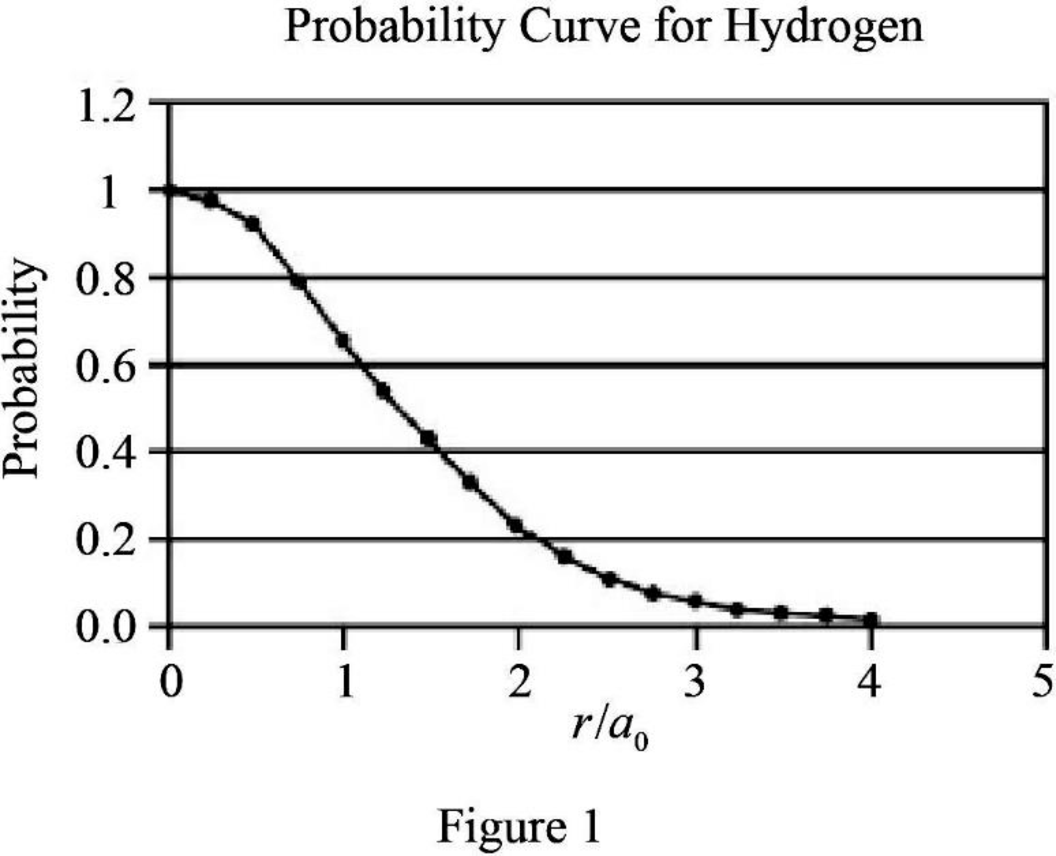
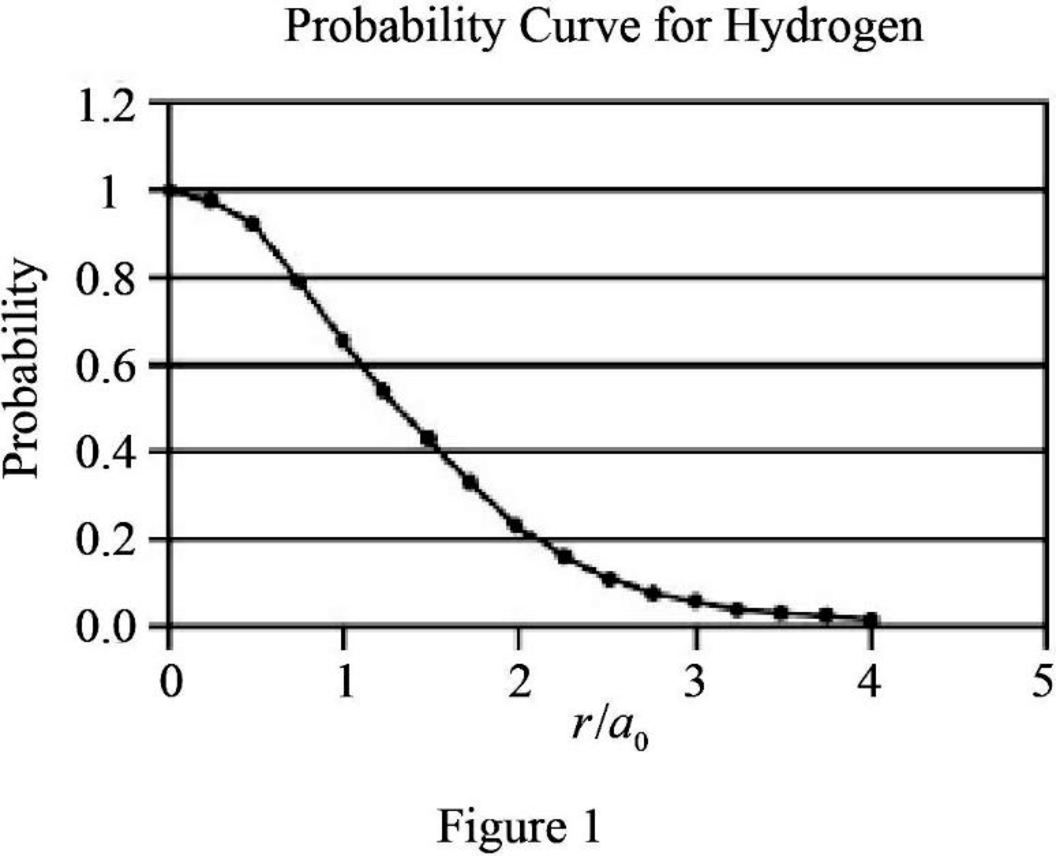
Explanation of Solution
The expression for probability as a function of
The expression is exponential in nature. The graph will be exponentially decreasing as the value of
Assume values between
Figure 1 below shows the plot between probability and
Conclusion:
Therefore, The graph between probability and
(c)
The value of
(c)
Answer to Problem 78AP
The value of
Explanation of Solution
The probability to detect an electron inside or outside a sphere of radius
Use expression for probability derived in part (a).
Substitute
Put
Conclusion:
Equation (VIII) is a transcendental equation. Solving it the value of
Therefore, the value of
Want to see more full solutions like this?
Chapter 42 Solutions
Physics For Scientists And Engineers With Modern Physics, 9th Edition, The Ohio State University
- A square metal sheet 2.5 cm on a side and of negligible thickness is attached to a balance and inserted into a container of fluid. The contact angle is found to be zero, as shown in Figure a, and the balance to which the metal sheet is attached reads 0.42 N. A thin veneer of oil is then spread over the sheet, and the contact angle becomes 180°, as shown in Figure b. The balance now reads 0.41 N. What is the surface tension of the fluid? x Your response differs from the correct answer by more than 10%. Double check your calculations. N/m a barrow_forwardA helium-filled balloon (whose envelope has a mass of m₁ = 0.260 kg) is tied to a uniform string of length l = 2.70 m and mass m = 0.050 6 kg. The balloon is spherical with a radius of r = 0.399 m. When released in air of temperature 20°C and density Pair = 1.20 kg/m³, it lifts a length h of string and then remains stationary as shown in the figure below. We wish to find the length of string lifted by the balloon. He (a) When the balloon remains stationary, what is the appropriate analysis model to describe it? Oa particle in equilibrium model a particle under constant acceleration model a particle under constant velocity model the ideal fluid model (b) Write a force equation for the balloon from this model in terms of the buoyant force B, the weight F of the balloon, the weight Fe of the helium, and the weight F of the segment of string of length h. (Use any variable or symbol stated above along with the following as necessary: π. Follow the sign convention that upward is the positive…arrow_forwardAssume that if the shear stress in steel exceeds about 4.00 × 108 N/m², the steel ruptures. (a) Determine the shearing force necessary to shear a steel bolt 1.50 cm in diameter. (No Response) N (b) Determine the shearing force necessary to punch a 1.50-cm-diameter hole in a steel plate 0.650 cm thick. (No Response) Narrow_forward
- = = You are preparing your house for a party with your classmates and friends, and want to set up an impressive light display to entertain them. From your study of fluids, you have come up with the idea based on the water flowing from the tank in the figure. You set up the tank as shown in the figure, filled to a depth h 1.15 m, and sitting on a stand of height { 0.300 m. You punch a hole in the tank at a height of Y1 = 0.102 m above the stand. (Ignore the thickness of the tank in your calculation.) You want to punch a second hole higher on the tank so that the streams of water from the two holes arrive at the same position on the table, in a catch basin at a distance d from the right edge of the stand. A pump will continuously carry water from the catch basin back up to the top of the tank to keep the water level fixed. Then, you will use laser pointers on the left side of the tank to light the two streams of water, which will capture the light (see the section on total internal…arrow_forwardA square metal sheet 2.5 cm on a side and of negligible thickness is attached to a balance and inserted into a container of fluid. The contact angle is found to be zero, as shown in Figure a, and the balance to which the metal sheet is attached reads 0.42 N. A thin veneer of oil is then spread over the sheet, and the contact angle becomes 180°, as shown in Figure b. The balance now reads 0.41 N. What is the surface tension of the fluid? N/m aarrow_forwardSucrose is allowed to diffuse along a 12.0-cm length of tubing filled with water. The tube is 6.1 cm² in cross-sectional area. The diffusion coefficient is equal to 5.0 × 10-10 m²/s, and 8.0 × 10−14 x transported along the tube in 18 s. What is the difference in the concentration levels of sucrose at the two ends of the tube? .00567 kg isarrow_forward
- need help part a and barrow_forwardComplete the table below for spherical mirrors indicate if it is convex or concave. Draw the ray diagrams S1 10 30 S1' -20 20 f 15 -5 Marrow_forwardA particle with a charge of − 5.20 nC is moving in a uniform magnetic field of (B→=−( 1.22 T )k^. The magnetic force on the particle is measured to be(F→=−( 3.50×10−7 N )i^+( 7.60×10−7 N )j^. Calculate the scalar product v→F→. Work the problem out symbolically first, then plug in numbers after you've simplified the symbolic expression.arrow_forward
- Need help wity equilibrium qestionarrow_forwardneed answer asap please thanks youarrow_forwardA man slides two boxes up a slope. The two boxes A and B have a mass of 75 kg and 50 kg, respectively. (a) Draw the free body diagram (FBD) of the two crates. (b) Determine the tension in the cable that the man must exert to cause imminent movement from rest of the two boxes. Static friction coefficient USA = 0.25 HSB = 0.35 Kinetic friction coefficient HkA = 0.20 HkB = 0.25 M₁ = 75 kg MB = 50 kg P 35° Figure 3 B 200arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning
Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning





