Chapter 4.2, Problem 32P

Survey: Customer Loyalty Are customers more loyal in the east or in the west? The following table is based on information from Trends in the United States, published by the Food Marketing Institute, Washington, D.C. The columns represent length of customer loyalty (in years) at a primary supermarket. The rows represent regions of the United States.

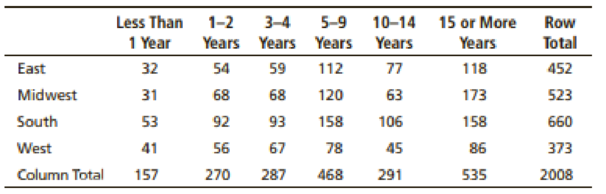
What is the probability that a customer chosen at random

1. (a) has been loyal 10 to 14 years?
2. (b) has been loyal 10 to 14 years, given that he or she is from the east?
3. (c) has been loyal at least 10 years?
4. (d) has been loyal at least 10 years, given that he or she is from the west?
5. (e) is from the west, given that he or she has been loyal less than 1 year?
6. (f) is from the south, given that he or she has been loyal less than 1 year?
7. (g) has been loyal 1 or more years, given that he or she is from the east?
8. (h) has been loyal 1 or more years, given that he or she is from the west?
9. (i) Are the events “from the east” and “loyal 15 or more years” independent? Explain.

To determine

Find the probability that a customer chosen at random has been loyal 10 to 14 years.

Answer to Problem 32P

The the probability that a customer chosen at random has been loyal 10 to 14 years is 0.1449.

Explanation of Solution

From the given Table, the number of customers in the 10 to 14 years is 291.

The total number of customers is 2042. That is, $f=291$ and $n=2,008$

The probability that a chosen customer at random has been loyal 10 to 14 years is as follows:

$\begin{array}{c}P\left(10\text{ to }14\text{ years}\right)=\frac{f}{n}\\ =\frac{291}{2,008}\\ \approx 0.1449\end{array}$

Thus, the probability that a customer chosen at random has been loyal 10 to 14 years is 0.1449.

To determine

Compute theprobability that a chosen customer at random has been loyal 10 to 14 years, given that he or she is from the east.

Answer to Problem 32P

The probability that a chosen customer at random has been loyal 10 to 14 years, given that he or she is from the east will be 0.1704.

Explanation of Solution

The probability that a chosen customer at random has been loyal 10 to 14 years, given that he or she is from the east as follows:

$\begin{array}{c}P\left(10\text{ to }14\text{ years /East}\right)=P\left(\frac{10\text{ to }14\text{ years andEast}}{\text{East}}\right)\\ =\frac{77}{452}\\ \approx 0.1704\end{array}$

Thus, the probability that a chosen customer at random has been loyal 10 to 14 years, given that he or she is from the east is 0.1704.

To determine

Find the probability that a chosen customer at random has been loyal at least 10 years.

Answer to Problem 32P

The probability that a chosen customer at random has been loyal at least 10 years is 0.4114.

Explanation of Solution

The probability that a chosen customer at random has been loyal at least 10 years is as follows:

$\begin{array}{c}P\left(\text{At least }10\text{years}\right)=P\left(10-14\text{years}\right)+P\left(15\text{ or More}\right)\\ =\frac{291}{2,008}+\frac{535}{2,008}\\ =\frac{826}{2,008}\\ \approx 0.4114\end{array}$

Thus, the probability that a chosen customer at random has been loyal at least 10 years is 0.4114.

To determine

Find the probability that a customer has been loyal at least 10 years, given that he or she is from the west.

Answer to Problem 32P

The the probability that a customer has been loyal at least 10 years, given that he or she is from the west is 0.3512.

Explanation of Solution

The probability that a customer has been loyal at least 10 years, given that he or she is from the west is computed as follows:

$\begin{array}{c}P\left(\text{At least }10\text{years/ West}\right)=P\left(10-14years/\text{West}\right)+P\left(15\text{ or More/West}\right)\\ =\frac{45}{373}+\frac{86}{373}\\ =\frac{131}{373}\\ \approx 0.3512\end{array}$

Thus, the probability that a customer has been loyal at least 10 years, given that he or she is from the west is 0.3512.

To determine

Find the probability that a customer is from the west, given that he or she has been loyal less than 1 year.

Answer to Problem 32P

The probability that a customer is from the west, given that he or she has been loyal less than 1 year is 0.2611.

Explanation of Solution

From the given Table, the number of customers in the west who have been loyal less than 1 year is 41 and the total number of customers in less than 1 year is 157.

The probability that a customer is from the west, given that he or she has been loyal less than 1 year is as follows:

$\begin{array}{c}P\left(\text{West/less than 1 year}\right)=\frac{41}{157}\\ =0.2611\end{array}$

Therefore, the probability that a customer is from the west, given that he or she has been loyal less than 1 year is 0.2611.

To determine

Find the probability that a customer is from the south, given that he or she has been loyal less than 1 year.

Answer to Problem 32P

The probability that a customer is from the south, given that he or she has been loyal less than 1 year is 0.3376.

Explanation of Solution

From the given Table, the number of customers in the south who have been loyal less than 1 year is 53 and the total number  of customers in the less than 1 year is 157.

The probability that a customer is from the south, given that he or she has been loyal less than 1 year is as follows:

$\begin{array}{c}P\left(\text{South/less than 1 year}\right)=\frac{53}{157}\\ =0.3376\end{array}$

Therefore, the probability that a customer is from the south, given that he or she has been loyal less than 1 year is 0.3376.

To determine

Find the probability that a customer has been loyal 1 or more years, given that he or she is from the east.

Answer to Problem 32P

The probability that a customer has been loyal 1 or more years, given that he or she is from the east is 0.9292.

Explanation of Solution

The probability that a customer has been loyal 1 or more years, given that he or she is from the east is computed as follows:

$\begin{array}{c}P\left(\text{1 or more years/East}\right)=1-P\left(\text{less than1year}/\text{East}\right)\\ =1-\frac{32}{452}\\ =\frac{452-32}{452}\\ =\frac{420}{452}\\ =0.9292\end{array}$

Thus, the probability that a customer has been loyal 1 or more years, given that he or she is from the east is 0.9292.

To determine

Compute the probability that a customer has been loyal 1 or more years, given that he or she is from the west.

Answer to Problem 32P

The probability that a customer has been loyal 1 or more years, given that he or she is from the west is 0.8900.

Explanation of Solution

The probability that a customer has been loyal 1 or more years, given that he or she is from the west is as follows:

$\begin{array}{c}P\left(\text{1 or more years/West}\right)=1-P\left(\text{less than1year}/\text{West}\right)\\ =1-\frac{41}{373}\\ =\frac{373-41}{373}\\ =\frac{332}{373}\\ =0.8900\end{array}$

Therefore, the probability that a customer has been loyal 1 or more years, given that he or she is from the west is 0.8900.

To determine

Explain whether the events “from the east” and “loyal 15 or more years” are independent.

Explanation of Solution

The independent condition for “from the east” and “loyal 15 or more years” is as follows:

$P\left(\text{East}\right)=P\left(\text{East/15 or more year}\right)$

Compute the value of $P\left(\text{East}\right)$ as follows:

$P\left(\text{East}\right)=\frac{452}{2,008}$

The value of $P\left(\text{East/15 or more years}\right)$ is as follows:

$\begin{array}{c}P\left(\text{East/15 or more years}\right)=\frac{118}{535}\\ =0.2205\end{array}$

Since the value of $P\left(\text{East}\right)$ is not equal to the value of $P\left(\text{East/15 or more years}\right)$. Thus, it can be said that the two events “from the east” and “loyal 15 or more years” are dependent.