Chapter 4.2, Problem 22P

Expand Your knowledge: Logarithmic Transformations. Exponential Growth Model There are several extensions of linear regression that apply to exponential growth and power law models. Problems 22-25 will outline some of these extensions. First of all. recall that a variable grows linearly over time if it adds a fixed increment during each equal period. Exponential growth occurs when a variable is multiplied by a fixed number during each period. This means that exponential growth increases by a fixed multiple or percentage of the previous amount. College algebra can be used to show that if a variable grows exponentially, then its logarithm grows linearly. The exponential growth model is $y=\alpha {\beta }^x$. where $\alpha \text{ and }\beta$ are fixed constants to be estimated from data.

How do we know when we are dealing with exponential growth, and how can we estimate $\alpha \text{ and }\beta$? Please read on. Populations of living things such as bacteria locusts, fish, panda bears, and so on lend to grow (or decline) exponentially. However, these populations can be restricted by outside limitations such as food, space, pollution, disease, hunting, and so on. Suppose we have data pairs (x, y) for which there is reason to believe the scatter plot is not linear but rather exponential, as described earlier. This means the increase in y values begins rather slowly but then seems to explode. Note: For exponential growth models, we assume all y > 0.

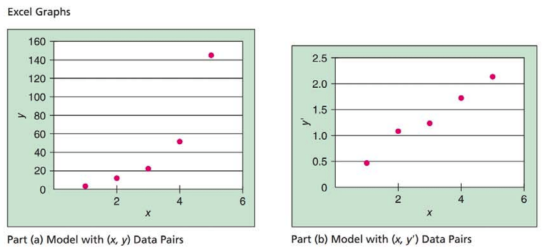
x	1	2	3	4	5
y	3	12	22	51	145

Consider the following data, where x = time in hours and y = number of bacteria in a laboratory culture at the end of x hours.

(a) Look at the Excel graph of the scatter diagram of the (x, y) data pairs. Do you think a straight line will be a good fit to these data? Do the y values seem almost to explode as time goes on?

(b) Now consider a transformation $y\text{'}=\text{ log }y$. We are using common logarithms of base 10 (however, natural logarithms of base e would work just as well).

x	1	2	3	4	5
y'=- log y	0.477	1.079	1.342	1.748	2.161

Look at the Excel graph of the scatter diagram of the (x. y') data pairs and compare this diagram with the diagram in part (a). Which graph appears to better fit a straight line?

(c) Use a calculator with regression keys to verify the linear regression equation for the (x, y) data pairs, $y=-50.3+32.3x$, with sample correlation coefficient r = 0.882.

(d) Use a calculator with regression keys to verify the linear regression equation for the (x, y') data pairs, $y\text{'}=0.150+0.404x$, with sample correlation coefficient r = 0.994. The sample correlation coefficient r = 0.882 for the (x, y) pairs is not bad. But the sample correlation coefficient r = 0.994 for the (x, y') pairs is a lot better!

(e) The exponential growth model is $y=\alpha {\beta }^x$. Let us use the results of part (d) to estimate $\alpha \text{ and }\beta$ for this strain of laboratory bacteria. The equation $y\text{'}=a+bx$ is the same as log $y=a+bx$. If we raise both sides of this equation to the power 10 and use some college algebra, we gel $y={10}^a{\left({10}^b\right)}^x.$ Thus, $\alpha ={10}^{\text{a}}\text{ and }\beta ={10}^{\text{b}}$. Use these results to approximate $\alpha \text{ and }\beta$ and write the exponential growth equation for our strain of bacteria.

Note: The TI-84Plus/TI-83Plu.s/TI-nspire calculators fully support the exponential growth model. Place the original x data in list LI and the corresponding y data in list L2. Then press STAT, followed by CALC, and scroll down to option 0: ExpReg. The output gives values for $\alpha ,\beta$. and the sample correlation coefficient r.