Trigonometry (11th Edition)
11th Edition
ISBN: 9780134217437
Author: Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 4, Problem 50RE
(a)
To determine
To calculate: The time between high tides in given graph.
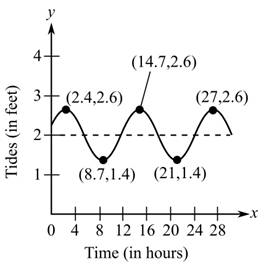
(b)
To determine
To calculate: The difference in water levels between high tide and low tide.
(c)
To determine
To calculate: The estimation of the tides for
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
what it means to have a change in amplitude and a change in period.
Pls help ASAP and pls show all steps and calculations.
Sinusoidal modeling: use your knowledge of amplitude, period, vertical translations, and horizontal translations along with your higher order of thinking skills to find functions that model the following.
Chapter 4 Solutions
Trigonometry (11th Edition)
Ch. 4.1 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.1 -
CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.1 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.1 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.1 -
5. The least positive number x for which cos x =...Ch. 4.1 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.1 - Concept Check Match each function with its graph...Ch. 4.1 - Concept Check Match each function with its graph...Ch. 4.1 -
Concept Check Match each function with its graph...Ch. 4.1 - Concept Check Match each function with its graph...
Ch. 4.1 - Concept Check Match each function with its graph...Ch. 4.1 - Concept Check Match each function with its graph...Ch. 4.1 -
Graph each function over the interval [ –2π, 2π]....Ch. 4.1 - Graph each function over the interval [ 2, 2]....Ch. 4.1 - Graph each function over the interval [2, 2]. Give...Ch. 4.1 -
Graph each function over the interval [–2π, 2π]....Ch. 4.1 - Graph each function over the interval [2,2]. Give...Ch. 4.1 -
Graph each function over the interval [–2π,2π]....Ch. 4.1 -
Graph each function over the interval [–2 π,2π]....Ch. 4.1 - Graph each function over the interval [–2π,2π]....Ch. 4.1 - Graph each function over the interval [2,2 ]. Give...Ch. 4.1 - Prob. 22ECh. 4.1 - Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 - Connecting Graphs with Equations Determine an...Ch. 4.1 - Connecting Graphs with Equations Determine an...Ch. 4.1 - Connecting Graphs with Equations Determine an...Ch. 4.1 - Connecting Graphs with Equations Determine an...Ch. 4.1 - Connecting Graphs with Equations Determine an...Ch. 4.1 - Connecting Graphs with Equations Determine an...Ch. 4.1 - Average Annual Temperature Scientists believe that...Ch. 4.1 - Blood Pressure Variation The graph gives the...Ch. 4.1 - Prob. 49ECh. 4.1 - Prob. 50ECh. 4.1 - Prob. 51ECh. 4.1 - Prob. 52ECh. 4.1 - Prob. 53ECh. 4.1 - Activity of a Nocturnal Animal Many activities of...Ch. 4.1 -
55. Atmospheric Carbon Dioxide At Mauna Loa....Ch. 4.1 - Atmospheric Carbon Dioxide Refer to Exercise 55....Ch. 4.1 -
57. Average Daily Temperature The temperature in...Ch. 4.1 - 58. Fluctuation in the Solar Constant The solar...Ch. 4.1 -
Musical Sound Waves Pure sounds produce single...Ch. 4.1 - Musical Sound Waves Pure sounds produce single...Ch. 4.1 - Prob. 61ECh. 4.1 - Prob. 62ECh. 4.1 - Prob. 63ECh. 4.1 - Prob. 64ECh. 4.1 - Prob. 65ECh. 4.1 - Prob. 66ECh. 4.2 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.2 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.2 - CONCEPT PREVIEW Fill in the blanks to correctly...Ch. 4.2 - CONCEPT PREVIEW Fill in the blanks to correctly...Ch. 4.2 -
CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.2 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.2 -
CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.2 - CONCEPT PREVIEW Fill in the blanks to correctly...Ch. 4.2 - Concept Check Match each function with its graph...Ch. 4.2 - Concept Check Match each function with its graph...Ch. 4.2 - Concept Check Match each function w ith its graph...Ch. 4.2 - Concept Check Match each function w ith its graph...Ch. 4.2 - Concept Check Match each function with its graph...Ch. 4.2 - Concept Check Match each function with its graph...Ch. 4.2 - Concept Check Match each function with its graph...Ch. 4.2 - Concept Check Match each function with its graph...Ch. 4.2 - The graphs of y = sin x + 1 and y = sin(x + 1) are...Ch. 4.2 - Concept Check Refer to Exercise 17. Which one of...Ch. 4.2 -
Concept Check Match each function in Column I...Ch. 4.2 - Concept Check Match each function in Column I with...Ch. 4.2 -
Concept Check Match each function in Column I...Ch. 4.2 - Concept Check Match each function in Column I with...Ch. 4.2 - Concept Check Fill in each blank with the word...Ch. 4.2 - Prob. 24ECh. 4.2 - Connecting Graphs with equations Each function...Ch. 4.2 - Connecting Graphs with Equations Each function...Ch. 4.2 -
Connecting Graphs with Equations Each function...Ch. 4.2 - Prob. 28ECh. 4.2 -
Find the amplitude, the period, any vertical...Ch. 4.2 -
Find the amplitude, the period, any vertical...Ch. 4.2 -
Find the amplitude, the period, any vertical...Ch. 4.2 -
Find the amplitude, the period, any vertical...Ch. 4.2 - Find the amplitude, the period, any vertical...Ch. 4.2 -
Find the amplitude, the period, any vertical...Ch. 4.2 - Find the amplitude, the period, any vertical...Ch. 4.2 - Find the amplitude, the period, any vertical...Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 -
Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 -
Graph each function over a one-period interval....Ch. 4.2 -
Graph each function over a one-period interval....Ch. 4.2 - Graph each function over a one-period interval....Ch. 4.2 - Graph each function over a one-period interval....Ch. 4.2 - Graph each function over a one-period interval....Ch. 4.2 -
Graph each function over a one-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 -
Graph each function over a two-period interval....Ch. 4.2 -
Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 -
Graph each function over a two-period interval....Ch. 4.2 -
Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 -
Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a one-period interval....Ch. 4.2 -
Graph each function over a one-period interval....Ch. 4.2 - Prob. 60ECh. 4.2 - Average Monthly Temperature The average monthly...Ch. 4.2 - Prob. 62ECh. 4.2 - Prob. 63ECh. 4.2 - Prob. 64ECh. 4.2 - Prob. 65ECh. 4.2 - Prob. 66ECh. 4.2 - Prob. 1QCh. 4.2 - Graph each function over a two-period interval....Ch. 4.2 - Prob. 3QCh. 4.2 - Prob. 4QCh. 4.2 - Prob. 5QCh. 4.2 - Graph each function over a two-period interval....Ch. 4.2 - Prob. 7QCh. 4.2 - Prob. 8QCh. 4.2 - Prob. 9QCh. 4.2 - Prob. 10QCh. 4.2 - Prob. 11QCh. 4.2 - Prob. 12QCh. 4.3 - 1. The least positive value x for which tan x = 0...Ch. 4.3 - The least positive value x for which cot x = 0 is...Ch. 4.3 - Concept Check Fill in each blank with the word...Ch. 4.3 - Concept Check Fill in each blank with the word...Ch. 4.3 - The negative value k with the greatest value for...Ch. 4.3 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.3 - Concept Check Match each function with its graph...Ch. 4.3 - Concept Check Match each function with its graph...Ch. 4.3 -
Concept Check Match each function with its...Ch. 4.3 - Concept Check Match each function with its graph...Ch. 4.3 - Concept CheckMatch each function with its graph...Ch. 4.3 - Concept Check Match each function with its graph...Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 -
Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 -
Graph each function over a one-period...Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 -
Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a two-period interval....Ch. 4.3 -
Graph each function over a two-period interval....Ch. 4.3 -
Graph each function over a two-period...Ch. 4.3 -
Graph each function over a two-period...Ch. 4.3 - Graph each function over a two-period interval....Ch. 4.3 - Graph each function over a two-period interval....Ch. 4.3 - Prob. 31ECh. 4.3 - Graph each function over a two-period interval....Ch. 4.3 - Graph each function over a two-period interval....Ch. 4.3 - Prob. 34ECh. 4.3 - Graph each function over a two-period interval....Ch. 4.3 - Prob. 36ECh. 4.3 - Graph each function over a two-period interval....Ch. 4.3 - Prob. 38ECh. 4.3 - Prob. 39ECh. 4.3 - Prob. 40ECh. 4.3 - Prob. 41ECh. 4.3 - Prob. 42ECh. 4.3 - Prob. 43ECh. 4.3 - Prob. 44ECh. 4.3 - Concept Check Decide whether each statement is...Ch. 4.3 - Concept CheckDecide whether each statement is true...Ch. 4.3 -
Concept Check Decide whether each statement is...Ch. 4.3 - Prob. 48ECh. 4.3 - Concept Check If c is any number, then how many...Ch. 4.3 - Prob. 50ECh. 4.3 - 51. Show that tan(–x) = –tan x by writing tan(–x)...Ch. 4.3 - 52. Show that cot (–x) = –cot x by writing cot...Ch. 4.3 - Prob. 53ECh. 4.3 - Prob. 54ECh. 4.3 - Prob. 55ECh. 4.3 - Prob. 56ECh. 4.3 - Prob. 57ECh. 4.3 - Prob. 58ECh. 4.3 - Prob. 59ECh. 4.3 - Prob. 60ECh. 4.3 - Prob. 61ECh. 4.3 - Prob. 62ECh. 4.4 - CONCEPT PREVIEW Match each description in Column I...Ch. 4.4 -
CONCEPT PREVIEW Match each description in...Ch. 4.4 -
CONCEPT PREVIEW Match each description in Column...Ch. 4.4 -
CONCEPT PREVIEW Match each description in Column...Ch. 4.4 -
CONCEPT PREVIEW Match each description in Column...Ch. 4.4 -
CONCEPT PREVIEW Match each description in Column...Ch. 4.4 - Concept Check Match each function with its graph...Ch. 4.4 - Concept Check Match each function with its graph...Ch. 4.4 - Concept Check Match each function with its graph...Ch. 4.4 - Concept Check Match each function with its graph...Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 -
Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Connecting Graphs with EquationsDetermine an...Ch. 4.4 - Connecting Graphs with Equations Determine an...Ch. 4.4 - Connecting Graphs with Equations Determine an...Ch. 4.4 - Connecting Graphs with Equations Determine an...Ch. 4.4 - Connecting Graphs with Equations Determine an...Ch. 4.4 - Prob. 30ECh. 4.4 - Concept CheckDecide whether each statement is true...Ch. 4.4 - Concept Check Decide whether each statement is...Ch. 4.4 - Concept CheckDecide whether each statement is true...Ch. 4.4 - Prob. 34ECh. 4.4 - 35. Concept Check If c is any number such that -1...Ch. 4.4 - Prob. 36ECh. 4.4 - 37. Show that sec (–x) = sec x by writing sec (–x)...Ch. 4.4 - Prob. 38ECh. 4.4 - Prob. 39ECh. 4.4 - (Modeling) Distance of a Rotating Beacon The...Ch. 4.4 - Prob. 41ECh. 4.4 - Prob. 42ECh. 4.4 - Prob. 43ECh. 4.4 - Prob. 44ECh. 4.4 - Prob. 45ECh. 4.4 - Prob. 46ECh. 4.4 - Prob. 1SECh. 4.4 - Prob. 2SECh. 4.4 - These summary exercises provide practice with the...Ch. 4.4 - Prob. 4SECh. 4.4 - Prob. 5SECh. 4.4 - Prob. 6SECh. 4.4 - Prob. 7SECh. 4.4 -
Graph each function over a two-period...Ch. 4.4 - Prob. 9SECh. 4.4 - Graph each function over a two-period...Ch. 4.5 - CONCEPT PREVIEW Refer to the equations in the...Ch. 4.5 - Prob. 2ECh. 4.5 - CONCEPT PREVIEW Refer to the equations in the...Ch. 4.5 - Prob. 4ECh. 4.5 - Prob. 5ECh. 4.5 - Prob. 6ECh. 4.5 - Spring Motion An object is attached to a coiled...Ch. 4.5 - Spring Motion Repeat Exercise 7, but assume that...Ch. 4.5 - 9. Voltage of an Electrical Circuit The voltage E...Ch. 4.5 - Prob. 10ECh. 4.5 - Particle Movement Write the equation and then...Ch. 4.5 - Prob. 12ECh. 4.5 -
13. Pendulum Motion What are the period P and...Ch. 4.5 - Prob. 14ECh. 4.5 - Spring Motion The formula for the up and down...Ch. 4.5 - Spring Motion (See Exercise 15.) A spring with...Ch. 4.5 - Spring Motion The position of a weight attached to...Ch. 4.5 - Spring Motion The position of a weight attached to...Ch. 4.5 - Spring Motion A weight attached to a spring is...Ch. 4.5 -
20. Spring Motion A weight attached to a spring...Ch. 4.5 -
(Modeling) Springs A weight on a spring has...Ch. 4.5 - Prob. 22ECh. 4.5 -
(Modeling) Springs A weight on a spring has...Ch. 4.5 -
(Modeling) Springs A weight on a spring has...Ch. 4.5 - Prob. 25ECh. 4.5 - Prob. 26ECh. 4.5 - Prob. 27ECh. 4.5 - Prob. 28ECh. 4.5 -
(Modeling) Spring Motion Consider the spring in...Ch. 4.5 - Prob. 30ECh. 4.5 - Prob. 31ECh. 4.5 - (Modeling) Spring Motion Consider the spring in...Ch. 4.5 - Prob. 33ECh. 4.5 - Prob. 34ECh. 4 - Concept Check Which one of the following...Ch. 4 - Prob. 2RECh. 4 - Prob. 3RECh. 4 - Prob. 4RECh. 4 - Prob. 5RECh. 4 - Prob. 6RECh. 4 - Prob. 7RECh. 4 - Prob. 8RECh. 4 -
For each function, give the amplitude, period,...Ch. 4 - Prob. 10RECh. 4 - Prob. 11RECh. 4 - Prob. 12RECh. 4 - Prob. 13RECh. 4 -
For each function, give the amplitude, period,...Ch. 4 - Prob. 15RECh. 4 - Prob. 16RECh. 4 - Prob. 17RECh. 4 - Prob. 18RECh. 4 - Prob. 19RECh. 4 - Prob. 20RECh. 4 - Prob. 21RECh. 4 - Prob. 22RECh. 4 - Prob. 23RECh. 4 - Prob. 24RECh. 4 - Prob. 25RECh. 4 - Prob. 26RECh. 4 - Prob. 27RECh. 4 - Prob. 28RECh. 4 - Prob. 29RECh. 4 - Prob. 30RECh. 4 - Prob. 31RECh. 4 - Prob. 32RECh. 4 - Graph each function over a one-period...Ch. 4 -
Graph each function over a one-period...Ch. 4 -
Graph each function over a one-period...Ch. 4 - Prob. 36RECh. 4 -
Graph each function over a one-period...Ch. 4 - Prob. 38RECh. 4 - Prob. 39RECh. 4 - Prob. 40RECh. 4 - Prob. 41RECh. 4 - Prob. 42RECh. 4 - (Modeling) Monthly Temperatures A set of...Ch. 4 - Prob. 44RECh. 4 - Prob. 45RECh. 4 - Prob. 46RECh. 4 - Prob. 47RECh. 4 - Prob. 48RECh. 4 - Prob. 49RECh. 4 - Prob. 50RECh. 4 - Prob. 51RECh. 4 - Prob. 52RECh. 4 - Prob. 53RECh. 4 - Prob. 54RECh. 4 - Prob. 55RECh. 4 - Prob. 56RECh. 4 - Prob. 57RECh. 4 - Prob. 58RECh. 4 - Prob. 1TCh. 4 - Prob. 2TCh. 4 - Prob. 3TCh. 4 - Prob. 4TCh. 4 - Prob. 5TCh. 4 - Prob. 6TCh. 4 - Prob. 7TCh. 4 - Prob. 8TCh. 4 - Prob. 9TCh. 4 - Prob. 10TCh. 4 - Prob. 11TCh. 4 - Prob. 12TCh. 4 - Average Monthly Temperature The average monthly...Ch. 4 -
14. Spring Motion The position of a weight...Ch. 4 - Prob. 15T
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, trigonometry and related others by exploring similar questions and additional content below.Similar questions
- Tide height as a function of time resembles a sinusoidal function during the time between low and high tide. At one such location on another planet with water, the tide has a high of 12.7 feet at 2 am and then the next low is -0.8 feet at 11 am (9 hours later). Find a formula for a sinusoidal function H(t) that gives the height tt hours after midnight.arrow_forwardSinusoidal modeling: use your knowledge of amplitude, period, vertical translations, and horizontal translations along with your higher order of thinking skills to find functions that model the following.arrow_forwardTide height as a function of time resembles a sinusoidal function during the time between low and high tide. At one such location on another planet with water, the tide has a high of 12.7 feet at 2 am and then the next low is -0.8 feet at 11 am (9 hours later). Find a formula for a sinusoidal function H(t) that gives the height t hours after midnight.arrow_forward
- Coastal areas experience tides which is where the ocean periodically gets to high and low points. Tides can be modeled with a sinusoidal (sine or cosine) function. At one beach, the high tide is 10 feet above mean sea level and the low tide is 10 feet below see level. The length of time between high and low tide is 5 hours. If high tide is at time t = Ohours, give the function H(t) that describes the height of the tide relative to sea level t hours after the high tide.arrow_forwardcan you write it out pleasearrow_forward2. The depth of water at the end of a pier varies with the tides throughout the day. On one day, the high tide occurs at 5:15 A.M. with a depth of 6.4 meters. The low tide occurs at 11:27 A.M. with a depth of 1.6 meters. a. Model the depth of water t hours after midnight using a cosine function b. Model the depth of water t hours after midnight a negative cosine function c. Model the depth of water t hours after midnight a sine function d. Find the depth of the water at 2:45 pm.arrow_forward
- Boarding for a ferris wheel occurs on a platform next to the 6:00 position (see image). The ferris wheel makes one full revolution every 5 minutes. (Assume the ferris wheel never stops rotating). The ferris wheel reaches a maximum height of 104 feet above the ground. Determine a cosine function that models the height h(feet) an occupant is above the ground at time t (minutes). Let t = 0 correspond to boarding the ferris wheel from the platform. h=h(t) = m 12 feet feetarrow_forwardA ferris wheel is 15 meters in diameter and boarded from a platform that is 5 meters above the ground. The six o'clock position on the ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 4 minutes. The function h = f(t) gives your height in meters above the ground t minutes after the wheel begins to turn. Amplitude -------- Minutes Midline ------ Minutes period ----- minutes How high are you off of the ground after 2 minutes --- meters answers are 7.5 12.5 4 20 please explain neatly , thank you !arrow_forwardExample • A wheel with a pointer is rotated and allowed to slow down and stop. When the wheel comes to rest, the angular position of the pointer is 8. A scale, 0<<360°, is marked with uniform increments around the rim of the wheel. Determine the PDF of e.arrow_forward
- Problem Solving 1. Consider the function y-3cosx-2x]-1. a. What is the amplitude of the function? b. What is the period? c. Describe the phase shift d. Describe the vertical translation e. Sketch the graph of the function for two cycles. 3arrow_forwardModeling Ocean Tides In one day, there are two high tides and two low tides in equally spaced intervals. The high tide is observed to be 6 feet above the average sea level. After 6 hours pass, the low tide occurs at 6 feet below the average sea level. In this task, you will model this occurrence using a trigonometric function by using x as a measurement of time. Assume the first high tide occurs at x = 0. Part E What is the height of the tide after 93 hours? 15pxarrow_forwardPls help ASAParrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
01 - What Is A Differential Equation in Calculus? Learn to Solve Ordinary Differential Equations.; Author: Math and Science;https://www.youtube.com/watch?v=K80YEHQpx9g;License: Standard YouTube License, CC-BY
Higher Order Differential Equation with constant coefficient (GATE) (Part 1) l GATE 2018; Author: GATE Lectures by Dishank;https://www.youtube.com/watch?v=ODxP7BbqAjA;License: Standard YouTube License, CC-BY
Solution of Differential Equations and Initial Value Problems; Author: Jefril Amboy;https://www.youtube.com/watch?v=Q68sk7XS-dc;License: Standard YouTube License, CC-BY