Fluid Mechanics
8th Edition
ISBN: 9780073398273
Author: Frank M. White
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 4, Problem 4.84P
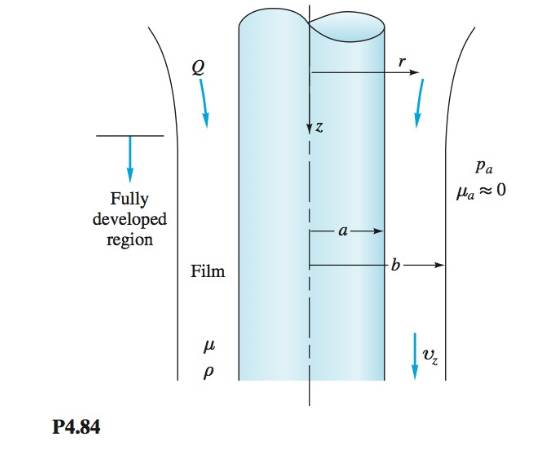
Consider a viscous film of liquid draining uniformly down the side of a vertical rod of radius a, as in Fig. P4.84. At some distance down the rod the film will approach a terminal or fully developed draining flow of constant outer radius b, with vz= vz(r),
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The flow pattern in bearing lubrication can be illustrated by
Fig. P4.83, where a viscous oil (p, µ) is forced into the gap
h(x) between a fixed slipper block and a wall moving at
velocity U. If the gap is thin, h< L, it can be shown that the
pressure and velocity distributions are of the form p = p(x),
u = u(y), v = w = 0. Neglecting gravity, reduce the
Navier-Stokes rquations .. to a single differential
equation for u(y). What are the proper boundary conditions?
Integrate and show that
1 dp ( – yh) + U(
и
2д dx
where h = h(x) may be an arbitrary, slowly varying gap
width. (
Oil
inlet
Fixed slipper
block
Oil
outlet
ho
h(x)
и (у)
Moving wall
A,B
P3.5 Water at 20°C flows through a 5-in-diameter smooth pipe
at a high Reynolds number, for which the velocity profile
is approximated by u = U.(v/R)/8, where U, is the cen-
terline velocity, R is the pipe radius, and y is the distance
measured from the wall toward the centerline. If the cen-
terline velocity is 25 ft/s, estimate the volume flow rate
in gallons per minute.
Chapter 4 Solutions
Fluid Mechanics
Ch. 4 - Prob. 4.1PCh. 4 - Flow through the converging nozzle in Fig. P4.2...Ch. 4 - Prob. 4.3PCh. 4 - Prob. 4.4PCh. 4 - Prob. 4.5PCh. 4 - Prob. 4.6PCh. 4 - Prob. 4.7PCh. 4 - P4.8 When a valve is opened, fluid flows in...Ch. 4 - An idealized incompressible flow has the proposed...Ch. 4 - A two-dimensional, incompressible flow has the...
Ch. 4 - Prob. 4.11PCh. 4 - Prob. 4.12PCh. 4 - Prob. 4.13PCh. 4 - Prob. 4.14PCh. 4 - What is the most general form of a purely radial...Ch. 4 - Prob. 4.16PCh. 4 - An excellent approximation for the two-dimensional...Ch. 4 - Prob. 4.18PCh. 4 - A proposed incompressible plane flow in polar...Ch. 4 - Prob. 4.20PCh. 4 - Prob. 4.21PCh. 4 - Prob. 4.22PCh. 4 - Prob. 4.23PCh. 4 - Prob. 4.24PCh. 4 - An incompressible flow in polar coordinates is...Ch. 4 - Prob. 4.26PCh. 4 - Prob. 4.27PCh. 4 - P4.28 For the velocity distribution of Prob. 4.10,...Ch. 4 - Prob. 4.29PCh. 4 - Prob. 4.30PCh. 4 - Prob. 4.31PCh. 4 - Prob. 4.32PCh. 4 - Prob. 4.33PCh. 4 - Prob. 4.34PCh. 4 - P4.35 From the Navier-Stokes equations for...Ch. 4 - A constant-thickness film of viscous liquid flows...Ch. 4 - Prob. 4.37PCh. 4 - Prob. 4.38PCh. 4 - Reconsider the angular momentum balance of Fig....Ch. 4 - Prob. 4.40PCh. 4 - Prob. 4.41PCh. 4 - Prob. 4.42PCh. 4 - Prob. 4.43PCh. 4 - Prob. 4.44PCh. 4 - Prob. 4.45PCh. 4 - Prob. 4.46PCh. 4 - Prob. 4.47PCh. 4 - Consider the following two-dimensional...Ch. 4 - Prob. 4.49PCh. 4 - Prob. 4.50PCh. 4 - Prob. 4.51PCh. 4 - Prob. 4.52PCh. 4 - Prob. 4.53PCh. 4 - P4.54 An incompressible stream function is...Ch. 4 - Prob. 4.55PCh. 4 - Prob. 4.56PCh. 4 - A two-dimensional incompressible flow field is...Ch. 4 - P4.58 Show that the incompressible velocity...Ch. 4 - Prob. 4.59PCh. 4 - Prob. 4.60PCh. 4 - An incompressible stream function is given by...Ch. 4 - Prob. 4.62PCh. 4 - Prob. 4.63PCh. 4 - Prob. 4.64PCh. 4 - Prob. 4.65PCh. 4 - Prob. 4.66PCh. 4 - A stream function for a plane, irrotational, polar...Ch. 4 - Prob. 4.68PCh. 4 - A steady, two-dimensional flow has the following...Ch. 4 - A CFD model of steady two-dimensional...Ch. 4 - Consider the following two-dimensional function...Ch. 4 - Prob. 4.72PCh. 4 - Prob. 4.73PCh. 4 - Prob. 4.74PCh. 4 - Given the following steady axisymmetric stream...Ch. 4 - Prob. 4.76PCh. 4 - Prob. 4.77PCh. 4 - Prob. 4.78PCh. 4 - Prob. 4.79PCh. 4 - Oil, of density and viscosity , drains steadily...Ch. 4 - Prob. 4.81PCh. 4 - Prob. 4.82PCh. 4 - P4.83 The flow pattern in bearing Lubrication can...Ch. 4 - Consider a viscous film of liquid draining...Ch. 4 - Prob. 4.85PCh. 4 - Prob. 4.86PCh. 4 - Prob. 4.87PCh. 4 - The viscous oil in Fig. P4.88 is set into steady...Ch. 4 - Oil flows steadily between two fixed plates that...Ch. 4 - Prob. 4.90PCh. 4 - Prob. 4.91PCh. 4 - Prob. 4.92PCh. 4 - Prob. 4.93PCh. 4 - Prob. 4.94PCh. 4 - Two immiscible liquids of equal thickness h are...Ch. 4 - Prob. 4.96PCh. 4 - Prob. 4.97PCh. 4 - Prob. 4.98PCh. 4 - For the pressure-gradient flow in a circular tube...Ch. 4 - W4.1 The total acceleration of a fluid particle is...Ch. 4 - Is it true that the continuity relation, Eq....Ch. 4 - Prob. 4.3WPCh. 4 - Prob. 4.4WPCh. 4 - W4.5 State the conditions (there are more than...Ch. 4 - Prob. 4.6WPCh. 4 - W4.7 What is the difference between the stream...Ch. 4 - Under what conditions do both the stream function...Ch. 4 - Prob. 4.9WPCh. 4 - Consider an irrotational, incompressible,...Ch. 4 - Prob. 4.1FEEPCh. 4 - Prob. 4.2FEEPCh. 4 - Prob. 4.3FEEPCh. 4 - Given the steady, incompressible velocity...Ch. 4 - Prob. 4.5FEEPCh. 4 - Prob. 4.6FEEPCh. 4 - C4.1 In a certain medical application, water at...Ch. 4 - Prob. 4.2CP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- A constant-thickness film of viscous liquid flows in laminarmotion down a plate inclined at angle θ , as in Fig. P4.36.The velocity profile isu = Cy(2h - y) υ = w = 0Find the constant C in terms of the specifi c weight andviscosity and the angle θ . Find the volume fl ux Q per unitwidth in terms of these parameters.arrow_forwardP4.41 As mentioned in P4.41, is the velocity profile for laminar flow between two plates, as in Fig. u = 4umaxy(hy) h² v=w=0 If the wall temperature is Tw at both walls, use the incompressible-flow energy equation (4.75) to solve for the temperature distribution T(y) between the walls for steady flow. y = h y = 0 y \u{y) T(y) Twarrow_forwardA pipe inclined at 45° to the horizontal (Fig. 2) converges over a length l of 2 m from a diameterd1 of 200 mm to a diameter d2 of 100 mm at the upper end. Oil of relative density 0.9 flowsthrough the pipe at a mean velocity ?̅1 at the lower end of 2 m/s. Find the pressure differenceacross the 2 m length ignoring any loss of energy, and the difference in level that would beshown on a mercury manometer connected across this length. The relative density of mercury is 13.6 and the leads to the manometer arefilled with the oil.arrow_forward
- Don't give handwritten solution.arrow_forwardLiquid drains from a small hole in a tank, as shown inFig. P4.60, such that the velocity fi eld set up is given byυ r ≈ 0, υ z ≈ 0, υ θ ≈ KR 2 / r , where z = H is the depth of thewater far from the hole. Is this fl ow pattern rotational orirrotational? Find the depth z C of the water at the radiusr = R .arrow_forwardP.4.12 Oil of density 950 kg/m and viscosity 102 Ns/m² is to be pumped 10 km through a pipeline and the pressure drop must not exceed 2x10S N/m. What is the minimum diameter of pipe, which will be suitable, if a flowrate of 50 ton/h is to be maintained? Assume the pipe wall to be smooth. Use either a pipe friction chart or the Blasius equation f= 0.079/ Re4. Ans. d = 0.193 m D412arrow_forward
- An incompressible fluid (water) flows steadily from an open tank. The elevation of point 1 is 10.0m, and the elevation of point 2 and 3 is 2.00m. The cross-sectional area at point 2 is 0.0680 m^2, at point 3 it is 0.0360 m^2. The area of the tank is very large compared to the cross-sectional area of the pipe. Assuming that Bernoulli’s equation applies, compute: The gauge pressure at point 2.arrow_forward6) Air flow though the device shown in figure. Select which set of the following conditions is TRUE assuming incompressible non-viscous steady flow (a) p4 v3 (c) p2>p3; v2 > v3 (e) p4> pl; v4 pl; vl > v3 (d) p4 vl 2 ⇒OUTarrow_forwardTwo immiscible liquids of equal thickness h are beingsheared between a fixed and a moving plate, as in Fig. .Gravity is neglected, and there is no variation with x . Findan expression for ( a ) the velocity at the interface and ( b ) theshear stress in each fluid. Assume steady laminar flow.arrow_forward
- 2. (i) Water flows through a 5cm diameter pipe which has a 180° vertical bend, as in the Figure below. The total length of pipe between flanges 1 and 2 is 75 cm. When the weight flow rate is 230 N/s, p, = 165 kPa, and p2 = 134 kPa. Neglecting pipe weight, determine the total force which the flanges must withstand for this flow. (ii) Please describe Reynolds Transport Theorem and its physical meaning.arrow_forwardb) A Newtonian fluid flows in an annular space created by a concentric pipe of radius R, and a rod of radius R;, as shown in Figure Q1(b). The rod is moving at a constant velocity V, while the pipe is stationary. The flow is steady, laminar and incompressible and there is no forced pressure gradient driving the flow. Assuming the velocity components in the radial and tangential directions are zero and ignoring the effects of gravity, derive an expression for the velocity field in the annular space. R. R: Figure Q1(b)arrow_forward5. Is a flow for which u = 3 m: s-1, v= 8x s' possible in an incompressible fluid? Can a potential function exist?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Intro to Compressible Flows — Lesson 1; Author: Ansys Learning;https://www.youtube.com/watch?v=OgR6j8TzA5Y;License: Standard Youtube License