
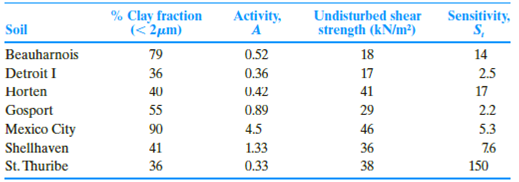
The properties of seven different clayey soils are shown below (Skempton and Northey, 1952). Investigate the relationship between the strength and plasticity characteristics by performing the following tasks:
a. Estimate the plasticity index for each soil using Skempton’s definition of activity [Eq. (4.28)].
b. Estimate the probable mineral composition of the clay soils based on PI and A (use Table 4.3)
c. Sensitivity (St) refers to the loss of strength when the soil is remolded or disturbed. It is defined as the ratio of the undisturbed strength (τf-undisturbed) to the remolded strength (τf-remolded)) at the same moisture content [Eq. (12.49)]. From the given data, estimate τf-remolded for the clay soils.
d. Plot the variations of undisturbed and remolded shear strengths with the activity, A, and explain the observed behavior.
(a)
Find the plasticity index for each soil using Skempton’s definition of activity.
Explanation of Solution
Determine the plasticity index of the Beauharnais soil using the relation.
Here, A is an activity.
Substitute 0.52 for A and 79 for % of clay–size fraction, by weight.
Similarly, calculate the plasticity index for the remaining soils.
Determine the remolded shear strength of the Beauharnais soil using the relation.
Here,
Substitute
Similarly, calculate the remolded shear strength of the remaining soils.
Summarize the calculated values of plasticity index and the remolded shear strength as in Table 1.
| Soil | % Clay fraction | Activity A | Plasticity Index |
| Beauharnois | 79 | 0.52 | 41.08 |
| Detroit I | 36 | 0.36 | 12.96 |
| Horten | 40 | 0.42 | 16.80 |
| Gosport | 55 | 0.89 | 48.95 |
| Mexico City | 90 | 4.5 | 405 |
| Shell haven | 41 | 1.33 | 54.53 |
| St.Thuribe | 36 | 0.33 | 11.88 |
(b)
Find the probable mineral composition of the clay soils based on PI and A.
Explanation of Solution
Determine the probable mineral composition of the clay soils based on PI and A.
Refer Table 4.3, “Typical values of liquid limit, plastic limit, and activity of some clay minerals” in the textbook.
Take the mineral composition of the Beauharnois soil as Illite for the activity value of 0.52 and the plasticity index value of 41.08.
Therefore, the mineral composition of Beauharnois soil is Illite.
Similarly, calculate the probable mineral composition of the remaining soils.
Summarize the calculated values of mineral composition as in Table (2).
| Soil | Activity A | Plasticity Index | Mineral composition |
| Beauharnois | 0.52 | 41.08 | Illite |
| Detroit I | 0.36 | 12.96 | Kaolinite |
| Horten | 0.42 | 16.80 | Kaolinite |
| Gosport | 0.89 | 48.95 | Illite |
| Mexico City | 4.5 | 405 | Montmorillonite |
| Shell haven | 1.33 | 54.53 | Montmorillonite |
| St.Thuribe | 0.33 | 11.88 | Kaolinite |
(c)
Find the remoulded shear strength of the clay soil.
Explanation of Solution
Determine the remoulded shear strength of the Beauharnais soil using the relation.
Here,
Substitute
Similarly, calculate the remolded shear strength of the remaining soils.
Summarize the calculated values of remolded shear strength as in Table 3.
| Soil | Activity A | Undisturbed Shear strength | Sensitivity |
Remoulded Shear strength |
| Beauharnois | 0.52 | 18 | 14 | 1.3 |
| Detroit I | 0.36 | 17 | 2.5 | 6.8 |
| Horten | 0.42 | 41 | 17 | 2.4 |
| Gosport | 0.89 | 29 | 2.2 | 13.2 |
| Mexico City | 4.5 | 46 | 5.3 | 8.7 |
| Shell haven | 1.33 | 36 | 7.6 | 4.7 |
| St.Thuribe | 0.33 | 38 | 150 | 0.3 |
(d)
Plot the variations of undisturbed and remolded shear strengths with the activity A.
Explanation of Solution
Refer Table 3.
Plot the graph between the undisturbed, remolded shear strengths with the activity A as in Figure 1.
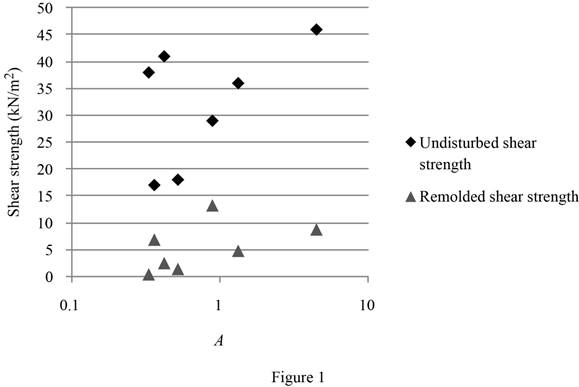
The shear strength of the clay obtains from two components, one is cohesion, which is the cementing force between particles, and second one is frictional resistance, which is mainly due to the particle movement of one particle over another. The cohesion contribution is greater to the shear strength, when the clay activity is greater. Although no reliable correlation can be developed from Figure 1, both the undisturbed and remolded shear strengths certainly show increasing trends as the activity increases.
Want to see more full solutions like this?
Chapter 4 Solutions
EBK PRINCIPLES OF GEOTECHNICAL ENGINEER
- For the I section prestressed concrete beam with a straight tendon shown in Fig below which is under the prestressing force, and U.D.L. Analyze the stresses at Mid- span at: A- transfer stage (due to initial prestress P. and self weight wo) B- at service stage. (due to effective prestress Pe and full loads) Check stresses with the ACI permissible stresses. Given: Initial prestress force Pi = 750 kN Effective prestress force Pe = 640 kN Wo (self) = 2.7 kN/m = W (D+L) 8 kN/m e = 130 mm I 5 10 mm² fci = 25 MPa (at transfer age), f' = 35 MPa (at service age) ASECTION 114 000 mm² W=4.75 kN/m |- 12 m F I 610mmarrow_forwardKindly help to provide explanation, examples and provide any useful link for citations and learning purposes. This is regarding building diagnosis.arrow_forwardDescribe the scientific of the arrival of enslaved Africans in America and how it has impacted American societyarrow_forward
- For the beam of cross section shown below, analyze the stresses at Mid-span at transfer and at service stages, Neglect losses. Use: f' =41.4 MPa and assume that concrete has attained strength of fci =34.5 MPa at the time of transfer. The initial prestress force is (Psi-1112 kN). The service deal load D.L = 3.65 kN/m (not include self weight of beam). The service live load L.L=14.6 kN/m. Use n=7. Check stresses with the ACI permissible stresses Determine the equivalent transformed section in compute A and I h=508 mm d=381 9.15 As= 1290 mm² 305arrow_forwardFor the prestressed concrete beam with a straight tendon shown in Fig below which is under the prestressing force of 1620 kN, Analyze the stresses at Mid-span at transfer stage. The uniformly distribution load (self weight) = 4.75 kN/m. Then draw the stress distribution across the section mid-span. W=4.75 kN/m Δ 7.3 m F= 1620 kN 750 mm I 230 mm 500 mmarrow_forward4.36 A pipe slopes upward in the direction of liquid flow at an angle of 30° with the horizontal. What is the pressure gradient in the flow direction along the pipe in terms of the specific weight of the liquid, y, if the liquid is decelerating (accelerating opposite to flow direction) at a rate of 0.3 g?arrow_forward
- 4.25 In this flow passage, the velocity is varying with time. The velocity varies with time at section A-A as 4m V-41/1-230/1 2.25- S to At time t = 0.50s, it is known that at section A-A the velocity gradient in the s direction is +2.1 m/s per meter. Given that to is 0.6 s and assuming quasi-1-D flow, answer the following questions for time t = 0.5 s: a. What is the local acceleration at A-A? b. What is the convective acceleration at A-A? A Diameter 50 cm Problem 4.25arrow_forwardCan you design a (Open Channel): -Most Efficient Section (Rectangle Shape) -Cost Estimate -Structural Analysis Design Requirements: Bed Slope= 1:1500 Manning's (n)= 0.015 Discharge: Q= 18 m^3/sarrow_forwardWhat is Highway engineeringarrow_forward
- Determine the vertical displacement of joint A. Each bar is made of steel and has the cross-sectional area shown. Take E = 29,000 ksi. Use the method of virtual work.arrow_forwardSketch the Energy Line and the Hydraulic Grade Line through the Venturi meter. Label the contribution of each term from bernoulli equationarrow_forward2. Design a storage and distribution system for the town of Waffle. The requirements are that fire protection shall be provided, the minimum water pressure at the top of the apartments is to be 240 kPa and the maximum system pressure is to be 550 kPa. The following assumptions may be used: Each of the four apartment buildings is occupied by 50 residents. Each apartment building is four stories high. Each story is 3 meters high. Each house is occupied by three residents. Average daily demand for the village is 500 Lpcd and the peak hourly demand factor is 6.2. Needed fire flow for the houses is 230 m3/h. and for apartment building is 500 m3/h, with 2 h duration. System pressure is to be provided from the elevated storage tank. Minor pressure losses in buildings may be ignored. The distribution system will not contain any loops. Assume that emergency supply (ES), fire department supply (FDS) or off peak pumping are not provided (they are all equal to zero). Provide the following…arrow_forward
 Principles of Geotechnical Engineering (MindTap C...Civil EngineeringISBN:9781305970939Author:Braja M. Das, Khaled SobhanPublisher:Cengage Learning
Principles of Geotechnical Engineering (MindTap C...Civil EngineeringISBN:9781305970939Author:Braja M. Das, Khaled SobhanPublisher:Cengage Learning Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Fundamentals of Geotechnical Engineering (MindTap...Civil EngineeringISBN:9781305635180Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Fundamentals of Geotechnical Engineering (MindTap...Civil EngineeringISBN:9781305635180Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781305081550Author:Braja M. DasPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781305081550Author:Braja M. DasPublisher:Cengage Learning Construction Materials, Methods and Techniques (M...Civil EngineeringISBN:9781305086272Author:William P. Spence, Eva KultermannPublisher:Cengage Learning
Construction Materials, Methods and Techniques (M...Civil EngineeringISBN:9781305086272Author:William P. Spence, Eva KultermannPublisher:Cengage Learning Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning





