Chapter 4, Problem 21P

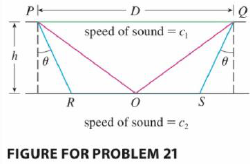
The speeds of sound c₁ in an upper layer and c₂ in a lower layer of rock and the thickness h of the upper layer can be determined by seismic exploration if the speed of sound in the lower layer is greater than the speed in the upper layer. A dynamite charge is detonated at a point P and the transmitted signals are recorded at a point Q, which is a distance D from P. The first signal to arrive at Q travels along the surface and takes T₁ seconds. The next signal travels from P to a point R, from R to S in the lower layer, and then to Q, taking T₂ seconds. The third signal is reflected off the lower layer at the midpoint O of RS and takes T₃ seconds to reach Q. (See the figure.)

(a) Express T₁, T₂, and T₃ in terms of D, h, c₁, c₂, and θ.

(b) Show that T₂, is a minimum when sin θ = c₁/c₂.

(c) Suppose that D = 1 km, T₁, = 0.26 s, T₂ = 0.32 s, and T₃ = 0.34 s. Find c₁, c₂, and h.

Note: Geophysicists use this technique when studying the structure of the earth’s crust, whether searching for oil or examining fault lines.