
Concept explainers
Suppose the single slit in Figure 38.4 is 6.00 cm wide and in front of a microwave source operating at 7.50 GHz. (a) Calculate the angle for the first minimum in the diffraction pattern. (b) What is the relative intensity l/lmax at 0 =- 15.0°? (c) Assume two such sources, separated laterally by 20.0 cm, are behind the slit. What must be the maximum distance between the plane of the sources and the slit if the diffraction patterns are to be resolved? In this case, the approximation sin θ ≈ tan 8 is not valid because of the relatively small value of a/λ.
(a)
The angle for the first minimum in the diffraction pattern.
Answer to Problem 38.77CP
The angle for the first minimum in the diffraction pattern is
Explanation of Solution
Given info: The width of the slit is
The expression of wavelength (
Here,
Substitute
Thus, the wavelength of the microwave source is
The expression of the condition for the first minimum in the diffraction pattern is,
Here,
Substitute
Thus, the angle for the first minimum in the diffraction pattern is
Conclusion:
Therefore, the angle for the first minimum in the diffraction pattern is
(b)
The relative intensity at
Answer to Problem 38.77CP
The relative intensity at
Explanation of Solution
Given info: The width of the slit is
The expression of the intensity variation in a diffraction pattern from a single slit is,
Here,
Rearrange the above equation for
Substitute
Thus, the relative intensity
Conclusion
Therefore, the relative intensity at
(c)
The maximum distance between the plane of the sources and the slit if the diffraction pattern are to be resolved.
Answer to Problem 38.77CP
The maximum distance between the plane of the sources and the slit if the diffraction pattern are to be resolved is
Explanation of Solution
Given info: The width of the slit is
The figure1 shows the given condition.
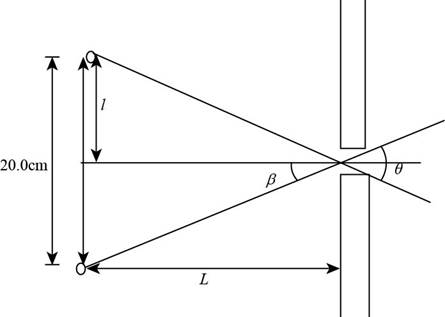
Figure (1)
Consider
The expression of distance (
Here,
Substitute
Thus, the distance of each source from the central line is
From figure1 the expression of distance (
The value of angle
Substitute
Substitute
Conclusion:
Therefore, The maximum distance between the plane of the sources and the slit if the diffraction pattern are to be resolved is
Want to see more full solutions like this?
Chapter 38 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- Radio telescopes are telescopes used for the detection of radio emission from space. Because radio waves have much longer wavelengths than visible light, the diameter of a radio telescope must be very large to provide good resolution. For example, the radio telescope in Penticton, BC in Canada, has a diameter of 26 m and can be operated at frequencies as high as 6.6 GHz. (a) What is the wavelength corresponding to this frequency? (b) What is the angular separation of two radio sources that can be resolved by this telescope? (c) Compare the telescope’s resolution with the angular size of the moon.arrow_forward(a) What is the minimum angular spread of a 633-nm wavelength He-Ne laser beam that is originally 1.00 mm in diameter? (b) If this laser is aimed at a mountain cliff 15.0 km away, how big will the illuminated spot be? (c) How big a spot would be illuminated on the moon, neglecting atmospheric effects? (This might be done to hit a corner reflector to measure the round-trip time and, hence, distance.)arrow_forwardSS-1 Coherent light of wavelength 675 nm passes through a narrow slit of width 0.0143 mm. The diffraction pattern is projected onto a viewing screen 1.08 m away from the slit. The intensity of the light at the center of the diffraction pattern is 175 W/m². (a) Draw a picture of the of situation descried in this problem. (b) Find the width of the central bright spot on the screen, in centimeters (cm). (c) Find the distance between the center of the diffraction pattern and the m = 4 minimum on the screen, in cm. (d) What is the intensity at a point on the screen 13.5 cm from the central maximum?arrow_forward
- A 475 nm wavelength spectral line is actually a doublet, 0.0043 nm separation. (a) What is the smallest number of lines that a diffraction network needs to have to separate this doublet in the 2nd order spectrum? (b) If this network is 10 cm long, in what direction will the line be observed in this spectrum? What will be the angular separation between the two components?arrow_forwardThe full width at half-maximum (FWHM) of a central diffraction maximum is defined as the angle between the two points in the pattern where the intensity is one-half that at the center of the pattern. (See figure (b).) (a) Does the intensity drop to one-half the maximum value when sin²α = a²/2? (b) Is a = 1.39 rad (about 80°) a solution to the transcendental equation of (a)? (c) Is the FWHM AÐ = 2sin¹(0.442 A/a), where a is the slit width? Calculate the FWHM of the central maximum for slit width (d) 1.17 A, (e) 5.03 A, and (f) 11.7 A. 20 20 Relative intensity 15 10 0.8 0.6 a=2 0.4 0.2 5 05 8 (degrees) (a) 10 15 20 20 Relative intensity 1.0 0.8 0.6 -A0- 0.4 0.2 a= 52 20 15 10 5 0 5 10 15 20 (degrees) (b)arrow_forwardTwo identical sources A and B emit in-phase plane radio waves with frequency 5.21E4 Hz and intensity 2.45E2 W/m2. A detector placed at location P closer to source B than source A detects a constructive interference. What is the minimum value of the path difference |AP–BP| (in m)?arrow_forward
- Light of wavelength 587.5 nm illuminates a slit of width 0.75 mm. (a) At what distance from the slit should a screen be placed if the first minimum in the diffraction pattern is to be 0.85 mm from the central maximum? (b) Calculate the width of the central maximum.arrow_forwardCoherent electromagnetic waves with wavelength l = 500 nm pass through two identical slits. The width of each slit is a, and the distance between the centers of the slits is d = 9.00 mm. (a) What is the smallest possible width a of the slits if the m = 3 maximum in the interference pattern is not present? (b) What is the next larger value of the slit width for which the m = 3 maximum is absent?arrow_forwardIf 580-nm light falls on a slit 0.05 mm wide, what is the full angular width of the central diffraction peak?arrow_forward
- Problem 2: Consider light that has its third minimum at an angle of 23.6° when it falls on a single slit of width 3.55 μm. Randomized Variables 9 = 23.6° w = 3.55 um D Find the wavelength of the light in nanometers. λ=1 sin() cos() cotan() asin() atan() acotan() tanh() cosh() O Degrees Hints: 2% deduction per hint. Hints remaining: 2 Submit tan() JU acos() E sinh() cotanh() Radians Hint ( + 7 8 9 4 5 6 1 0 VO BACKSPACE Feedback 2 3 All content © 2022 Expert TA, LLC DEL HOME END I give up! Feedback: 2% deduction per feedback. CLEARarrow_forwardTwo identical sources A and B emit in-phase plane radio waves with frequency 3.17E4 Hz and intensity 1.83E2 W/m2. A detector placed at location P closer to source B than source A detects a destructive interference. What is the minimum value of the path difference |AP–BP| (in m)?arrow_forwardLight of wavelength 633 nm is incident on a pair of identical stits of width 0.15 mm and center-to-center separation of 1.5 mm. The diffraction pattern is observed on a screen at distance 4 m. Calculate the spacing between consecutive zeros of intensity (in mm to 2 d.p.); and calculate how many peaks in total (on both sides) have intensity above 20 percent of the on-axis peak. (Hint: note sinc 2.0 = 0.454) The spacing of zeros is 1.69 mm, and the total number of peaks with at least 20 percent of central intensity isarrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax

