Concept explainers
Videos
(a)
The combination of gage block for (a).
Answer to Problem 20AR
The combination of blocks are
Explanation of Solution
Given:
Dimension is
Calculation:
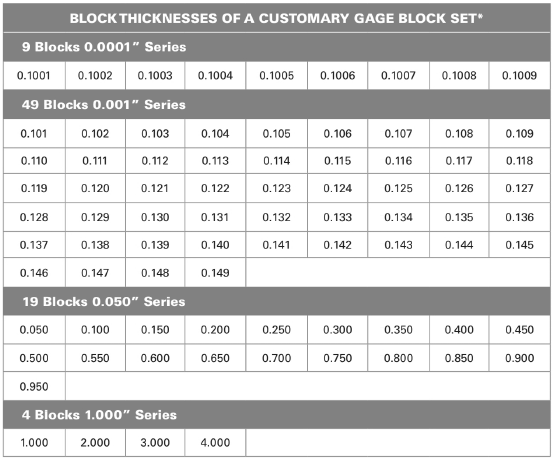
From above table:
The combination of the blocks are
Add all the dimensions of the blocks.
Thus, the combination of blocks are
Conclusion:
The combination of blocks are
(b)
The combination of gage block for (b).
Answer to Problem 20AR
The combination of blocks are
Explanation of Solution
Given:
Dimension is
Calculation:
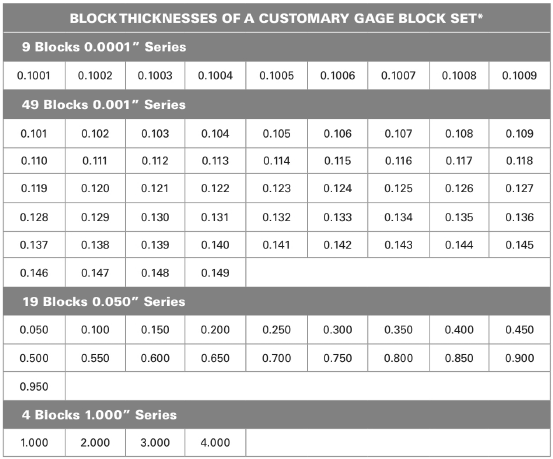
From above table:
The combination of the blocks are
Add all the dimensions of the blocks.
Thus, the combination of blocks are
Conclusion:
The combination of blocks are
(c)
The combination of gage block for (c).
Answer to Problem 20AR
The combination of blocks are
Explanation of Solution
Given:
Dimension is
Calculation:
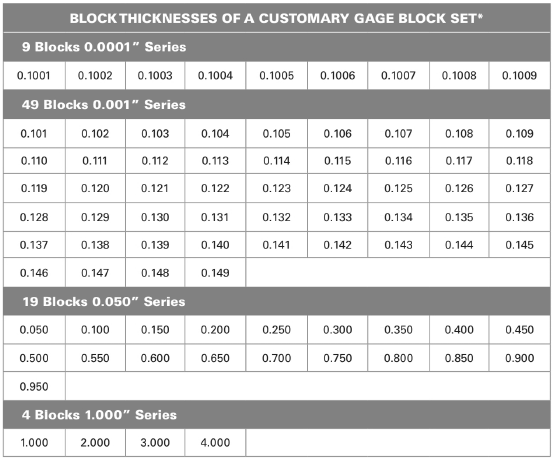
From above table:
The combination of the blocks are
Add all the dimensions of the blocks.
Thus, the combination of blocks are
Conclusion:
The combination of blocks are
(d)
The combination of gage block for (d).
Answer to Problem 20AR
The combination of blocks are
Explanation of Solution
Given:
Dimension is
Calculation:
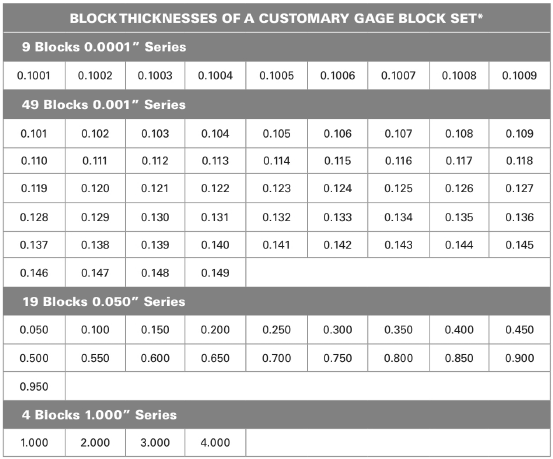
From above table:
The combination of the blocks are
Add all the dimensions of the blocks.
Thus, the combination of blocks are
Conclusion:
The combination of blocks are
(e)
The combination of gage block for (e).
Answer to Problem 20AR
The combination of blocks are
Explanation of Solution
Given:
Dimension is
Calculation:
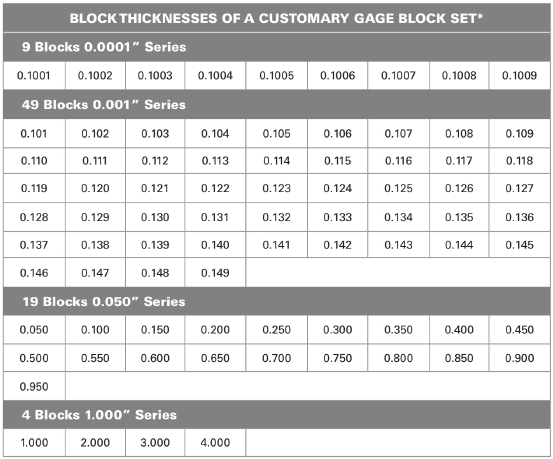
From above table:
The combination of the blocks are
Add all the dimensions of the blocks.
Thus, the combination of blocks are
Conclusion:
The combination of blocks are
(f)
The combination of gage block for (f).
Answer to Problem 20AR
The combination of blocks are
Explanation of Solution
Given:
Dimension is
Calculation:
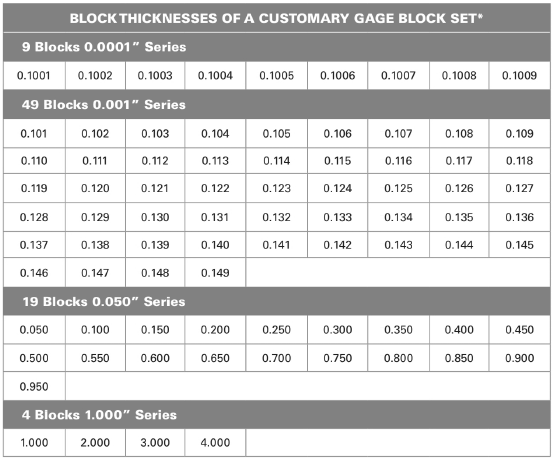
From above table:
The combination of the blocks are
Add all the dimensions of the blocks.
Thus, the combination of blocks are
Conclusion:
The combination of blocks are
(g)
The combination of gage block for (g).
Answer to Problem 20AR
The combination of blocks are
Explanation of Solution
Given:
Dimension is
Calculation:
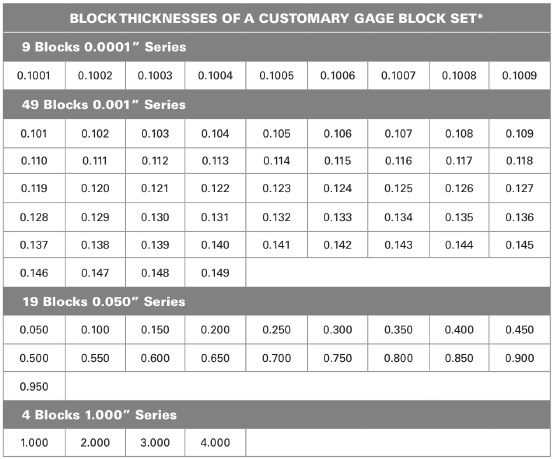
From above table:
The combination of the blocks are
Add all the dimensions of the blocks.
Thus, the combination of blocks are
Conclusion:
The combination of blocks are
(h)
The combination of gage block for (h).
Answer to Problem 20AR
The combination of blocks are
Explanation of Solution
Given:
Dimension is
Calculation:
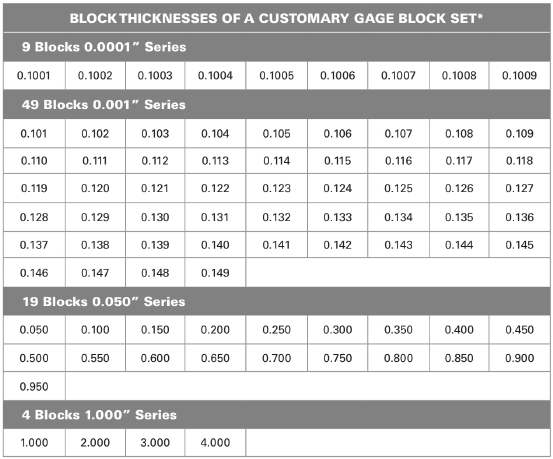
From above table:
The combination of the blocks are
Add all the dimensions of the blocks.
Thus, the combination of blocks are
Conclusion:
The combination of blocks are
Want to see more full solutions like this?
Chapter 38 Solutions
Mathematics For Machine Technology
- Advanced Functional Analysis Mastery Quiz Instructions: . No partial credit will be awarded; any mistake will result in a score of 0. ⚫ Submit your solution before the deadline. . Ensure your solution is detailed, and all steps are well-documented. • No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let X te a Banach space, and let T: XX be a linear operetor satisfying ||T|| - 1. Corsider the following tasks: 1. [Bounded Linear Operators] a. Prove that I is a bounded linear operator if and only if there exists a constant C such that ||T()||C|||| for all 2 € X. b. Show that if I' is a linear operator on a Banach space X and ||T||-1, then ||T(x)||||||| for all EX. 2. [Spectral Theorem] Let A be a self-adjoint operator on a Hibert space H. Assume that A has a non-empty spectrum. a. State and prove the Spectral…arrow_forwardAdvanced Mathematics Mastery Quiz Instructions: . No partial credit will be awarded; any mistake will result in a score of 0. Submit your solution before the deadline. . Ensure your solution is detailed, and all steps are well-documented. . . No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let the function f(x, y, z)=-42y+2ay" +22 tasks: and consider the following 1. [Critical Points and Classification] a. Find all critical points of f(x, y, z). b. Use the second partial derivative test to classify each critical point as a local minimum, local maximum, or saddle point. 2. [Directional Derivatives and Gradients] a. Compute the gradient vector Vf of f(x, y, z). b. Find the directional derivative of f at the point (1, 1, 1) in the direction of the vector v = (1,-2,3). 3. [Line Integral Evaluation] Consider the…arrow_forwardAdvanced Functional Analysis Mastery Quiz Instructions: . . No partial credit will be awarded; any mistake will result in a score of 0. Submit your solution before the deadline. . Ensure your solution is detailed, and all steps are well-documented. . . No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let X and Y be Banach spaces, and let T: XY be a bounded linear operator. Consider the following tasks: 1. [Baire's Category Theorem and Applications] a. State and prove Baire's Category Theorem for Banach spaces. Use the theorem to prove that a complete metric space cannot be the countable union of nowhere dense sets. b. Use Baire's Category Theorem to show that if T: XY is a bounded linear operator between Banach spaces, then the set of points in X where I' is continuous is a dense G8 set. 2. [Norms and…arrow_forward
- Advanced Functional Analysis Mastery Quiz Instructions: No partial credit will be awarded; any mistake will result in a score of 0. . Submit your solution before the deadline. . Ensure your solution is detailed, and all steps are well-documented. No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let X be a Banach space, and 7' be a bounded linear operator acting on X. Consider the following tasks: 1. [Operator Norm and Boundedness] a. Prove that the operator norm of a linear operator T': X →→ X is given by: ||T|| =sup ||T(2)|| 2-1 b. Show that if 'T' is a bounded linear operator on a Banach space, then the sequence {7"} converges to zero pointwise on any bounded subset of X if and only if ||T|| p, from X to X, where 4, (y)=(x, y), is a linear operator. b. Consider a sequence {} CX. Prove that if →→ 6(2)→→ (2)…arrow_forwardMathematics Challenge Quiz Instructions: • You must submit your solution before the deadline. • Any mistake will result in a score of 0 for this quiz. • Partial credit is not allowed; ensure your answer is complete and accurate. Problem Consider the parametric equations: x(t) = e cos(3t), y(t) = e sin(3t) fort Є R. 1. [Parametric Curve Analysis] a. Prove that the parametric curve represents a spiral by eliminating t and deriving the general equation in Cartesian form. b. Find the curvature (t) of the curve at any point 1. 2. [Integral Evaluation] For the region enclosed by the spiral between t = 0 and t =π, compute the area using the formula: where t₁ = 0 and t₂ = . A == √ √ ²x²(1)y (t) − y(t) x' (t)] dt 3. [Differential Equation Application] The curve satisfies a differential equation of the form: d'y da2 dy + P(x)+q(x)y = 0 a. Derive the explicit forms of p(x) and q(2). b. Verify your solution by substituting (t) and y(t) into the differential equation. 4. [Optimization and Limits]…arrow_forwardAdvanced Functional Analysis Mastery Quiz Instructions: No partial credit will be awarded: any mistake will result in a score of 0. Submit your solution before the deadline. Ensure your solution is detailed, and all stops are well-documented. No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let X and Y be Banach spaces, and let T: X →Y be a bounded linear operator. Consider the following tasks: 1. [Banach Fixed-Point Theorem] a State and prove the Banach Fixed-Point Theorem (Contraction Mapping Theorem). Provide a detailed explanation of how the theorem guarantees the existence of a unique fixed point for a contraction mapping on a complete metric space. b. Let T: X → X be a contraction mapping on X = R² with T(r. u) = (3.). Find the unique fixed point of T. 2. [Duality and the Hahn-Banach Theorem] a. State…arrow_forward
- Mathematics Mastery Quiz Instructions: • No partial credit will be awarded; any mistake will result in a score of 0. Submit your solution before the deadline. Ensure your solution is detailed and all steps are well-documented. Problem Let the function f(x, y) = x²y³ - 3x+y+ety and consider the following tasks: 1. [Critical Points and Classification] a. Find all critical points of f(x, y). b. Use the second partial derivative test to classify each critical point as a local minimum, local maximum, or saddle point. 2. [Line Integral Evaluation] Consider the vector field F(x, y) = (2x³y - y³ + e², 3x²y² - 4x³ + e³). a. Verify whether F is conservative. b. If conservative, compute the line integral of F along the curve C, parameterized as: C: Sx(t) = t² [y(t) = ln(t + 1)' tЄ [0,1].arrow_forwardAdvanced Functional Analysis Mastery Quiz Instructions: . No partial credit will be awarded; any mistake will result in a score of 0. . Submit your solution before the deadline. Ensure your solution is detailed, and all steps are well-documented. No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let X and Y be Banach spaces, and T: XY a bounded linear operator. Consider the following tasks: 1. [Bounded Linear Operators and Closed Graph Theorem] a. State and prove the Closed Graph Theorem, which asserts that if T: XY is a linear operator between Banach spaces and the graph of T' is closed in X x Y, then I' is bounded. b. Using the Closed Graph Theorem, show that if T: XY is an injective linear operator and the graph of 'I' is closed, then I' is bounded. 2. [Convergence and Strong vs Weak Topologies] a. Define…arrow_forwardPlease give a handwritten solution without use of AIarrow_forward
- Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell 
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL