Mathematics For Machine Technology
8th Edition
ISBN: 9781337798310
Author: Peterson, John.
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 38, Problem 11AR
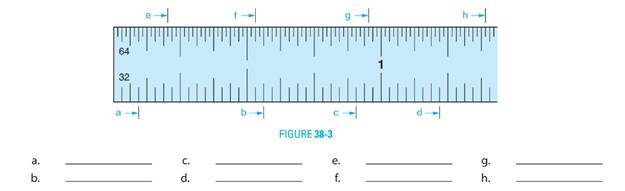
Read measurements a-h on the enlarged 32nds and 64th graduated fractional rule shown in Figure 38-3.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
pls help
In Problems 1-16 the indicated function y₁(x) is a solution of the
given differential equation. Use reduction of order or formula (5), as
instructed, to find a second solution y2(x).
1. y" - 4y' + 4y = 0; yı
=
e2x
-
Problem 3: For a short time, the 300-kg roller-coaster car with passengers is traveling along
the spiral track at a constant speed of v = 8 m/s with r = 15 m. If the track descends d =
6 m for every full revolution, 0 = 2π rad, determine the magnitudes of the components of
force which the track exerts on the car in the r, 0, and z directions. Neglect the size of the car.
Bonus: Develop a MATLAB program to solve for this problem.
Chapter 38 Solutions
Mathematics For Machine Technology
Ch. 38 - Prob. 1ARCh. 38 - Holes are to be drilled in the length of angle...Ch. 38 - Prob. 3ARCh. 38 - Prob. 4ARCh. 38 - For each of the exercises in the following table,...Ch. 38 - Prob. 6ARCh. 38 - Prob. 7ARCh. 38 - Prob. 8ARCh. 38 - The following problems require computations with...Ch. 38 - Prob. 10AR
Ch. 38 - Read measurements a-h on the enlarged 32nds and...Ch. 38 - Prob. 12ARCh. 38 - Prob. 13ARCh. 38 - Read measurements i-p on the enlarged 50ths and...Ch. 38 - Prob. 15ARCh. 38 - Prob. 16ARCh. 38 - Read the vernier caliper and height gage...Ch. 38 - Prob. 18ARCh. 38 - Prob. 19ARCh. 38 - Prob. 20ARCh. 38 - Prob. 21AR
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Problem 1: In a softball game, Peter throws a ball with an initial velocity Vo 120 km/h at an angle a. At Point B, the height of the ball is 0.7 m. determine (a) the angle a, (b) the angle 0 of the velocity when the ball reaches at Point B. Pr the tra rac 0.7 m B 14 m 0.58 marrow_forwardNot use ai pleasearrow_forwardLemma:- Let x = AX, Y° = By where A = B= 0 Bo then the linear system X = AX Y = BY are Linearly equivalent iff B=α.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Elementary Algebra
Algebra
ISBN:9780998625713
Author:Lynn Marecek, MaryAnne Anthony-Smith
Publisher:OpenStax - Rice University
01 - What Is A Differential Equation in Calculus? Learn to Solve Ordinary Differential Equations.; Author: Math and Science;https://www.youtube.com/watch?v=K80YEHQpx9g;License: Standard YouTube License, CC-BY
Higher Order Differential Equation with constant coefficient (GATE) (Part 1) l GATE 2018; Author: GATE Lectures by Dishank;https://www.youtube.com/watch?v=ODxP7BbqAjA;License: Standard YouTube License, CC-BY
Solution of Differential Equations and Initial Value Problems; Author: Jefril Amboy;https://www.youtube.com/watch?v=Q68sk7XS-dc;License: Standard YouTube License, CC-BY