Physics for Scientists and Engineers with Modern Physics
10th Edition
ISBN: 9781337553292
Author: Raymond A. Serway, John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 37.2, Problem 37.1QQ
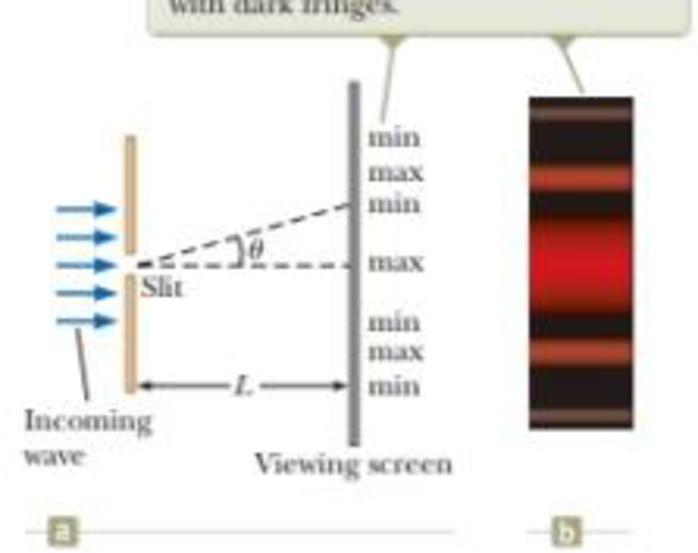
Suppose the slit width in Figure 37.4 is made half as wide. Does the central bright fringe (a) become wider, (b) remain the same, or (c) become narrower?
Figure 37.4 (a) Geometry for analyzing the Fraunhofer diffraction pattern of a single slit. (Drawing not to scale.) (b) Simulation of a single-slit Fraunhofer diffraction pattern.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Question B3
Consider the following FLRW spacetime:
t2
ds² = -dt² +
(dx²
+ dy²+ dz²),
t2
where t is a constant.
a)
State whether this universe is spatially open, closed or flat.
[2 marks]
b) Determine the Hubble factor H(t), and represent it in a (roughly drawn) plot as a function
of time t, starting at t = 0.
[3 marks]
c) Taking galaxy A to be located at (x, y, z) = (0,0,0), determine the proper distance to galaxy
B located at (x, y, z) = (L, 0, 0). Determine the recessional velocity of galaxy B with respect
to galaxy A.
d) The Friedmann equations are
2
k
8πG
а
4πG
+
a²
(p+3p).
3
a
3
[5 marks]
Use these equations to determine the energy density p(t) and the pressure p(t) for the
FLRW spacetime specified at the top of the page.
[5 marks]
e) Given the result of question B3.d, state whether the FLRW universe in question is (i)
radiation-dominated, (ii) matter-dominated, (iii) cosmological-constant-dominated, or (iv)
none of the previous. Justify your answer.
f)
[5 marks]
A conformally…
SECTION B
Answer ONLY TWO questions in Section B
[Expect to use one single-sided A4 page for each Section-B sub question.]
Question B1
Consider the line element
where w is a constant.
ds²=-dt²+e2wt dx²,
a) Determine the components of the metric and of the inverse metric.
[2 marks]
b) Determine the Christoffel symbols. [See the Appendix of this document.]
[10 marks]
c)
Write down the geodesic equations.
[5 marks]
d) Show that e2wt it is a constant of geodesic motion.
[4 marks]
e)
Solve the geodesic equations for null geodesics.
[4 marks]
Page 2
SECTION A
Answer ALL questions in Section A
[Expect to use one single-sided A4 page for each Section-A sub question.]
Question A1
SPA6308 (2024)
Consider Minkowski spacetime in Cartesian coordinates th
=
(t, x, y, z), such that
ds² = dt² + dx² + dy² + dz².
(a) Consider the vector with components V" = (1,-1,0,0). Determine V and V. V.
(b) Consider now the coordinate system x' (u, v, y, z) such that
u =t-x,
v=t+x.
[2 marks]
Write down the line element, the metric, the Christoffel symbols and the Riemann curvature
tensor in the new coordinates. [See the Appendix of this document.]
[5 marks]
(c) Determine V", that is, write the object in question A1.a in the coordinate system x'. Verify
explicitly that V. V is invariant under the coordinate transformation.
Question A2
[5 marks]
Suppose that A, is a covector field, and consider the object
Fv=AAμ.
(a) Show explicitly that F is a tensor, that is, show that it transforms appropriately under a
coordinate transformation.
[5 marks]
(b)…
Chapter 37 Solutions
Physics for Scientists and Engineers with Modern Physics
Ch. 37.2 - Suppose the slit width in Figure 37.4 is made half...Ch. 37.3 - Cats eyes have pupils that can be modeled as...Ch. 37.3 - Suppose you are observing a binary star with a...Ch. 37.4 - Ultraviolet light of wavelength 350 nm is incident...Ch. 37.6 - A polarizer for microwaves can be made as a grid...Ch. 37.6 - Prob. 37.6QQCh. 37 - Prob. 1PCh. 37 - Prob. 2PCh. 37 - Prob. 3PCh. 37 - In Figure 37.7, show mathematically how many...
Ch. 37 - Prob. 5PCh. 37 - What If? Suppose light strikes a single slit of...Ch. 37 - Prob. 7PCh. 37 - Coherent light of wavelength 501.5 nm is sent...Ch. 37 - Prob. 9PCh. 37 - Prob. 10PCh. 37 - What is the approximate size of the smallest...Ch. 37 - Prob. 12PCh. 37 - Prob. 13PCh. 37 - Prob. 14PCh. 37 - Impressionist painter Georges Seurat created...Ch. 37 - Prob. 16PCh. 37 - Consider an array of parallel wires with uniform...Ch. 37 - Prob. 18PCh. 37 - A grating with 250 grooves/mm is used with an...Ch. 37 - Show that whenever white light is passed through a...Ch. 37 - Light from an argon laser strikes a diffraction...Ch. 37 - Prob. 22PCh. 37 - You are working as a demonstration assistant for a...Ch. 37 - Prob. 24PCh. 37 - Prob. 25PCh. 37 - Prob. 26PCh. 37 - Prob. 27PCh. 37 - Prob. 28PCh. 37 - Prob. 29PCh. 37 - Prob. 30PCh. 37 - Prob. 31PCh. 37 - Prob. 32PCh. 37 - Prob. 33APCh. 37 - Laser light with a wavelength of 632.8 nm is...Ch. 37 - Prob. 35APCh. 37 - Prob. 36APCh. 37 - Prob. 37APCh. 37 - Prob. 38APCh. 37 - Prob. 39APCh. 37 - Prob. 40APCh. 37 - Prob. 41APCh. 37 - Prob. 42APCh. 37 - Prob. 43APCh. 37 - Prob. 44APCh. 37 - Prob. 45APCh. 37 - Prob. 46APCh. 37 - Prob. 47APCh. 37 - Prob. 48APCh. 37 - Two closely spaced wavelengths of light are...Ch. 37 - Prob. 50CPCh. 37 - Prob. 51CPCh. 37 - In Figure P37.52, suppose the transmission axes of...Ch. 37 - Prob. 53CP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- No chatgpt pls will upvote Iarrow_forwardHow would partial obstruction of an air intake port of an air-entrainment mask effect FiO2 and flow?arrow_forward14 Z In figure, a closed surface with q=b= 0.4m/ C = 0.6m if the left edge of the closed surface at position X=a, if E is non-uniform and is given by € = (3 + 2x²) ŷ N/C, calculate the (3+2x²) net electric flux leaving the closed surface.arrow_forward
- No chatgpt pls will upvotearrow_forwardsuggest a reason ultrasound cleaning is better than cleaning by hand?arrow_forwardCheckpoint 4 The figure shows four orientations of an electric di- pole in an external electric field. Rank the orienta- tions according to (a) the magnitude of the torque on the dipole and (b) the potential energy of the di- pole, greatest first. (1) (2) E (4)arrow_forward
- What is integrated science. What is fractional distillation What is simple distillationarrow_forward19:39 · C Chegg 1 69% ✓ The compound beam is fixed at Ę and supported by rollers at A and B. There are pins at C and D. Take F=1700 lb. (Figure 1) Figure 800 lb ||-5- F 600 lb بتا D E C BO 10 ft 5 ft 4 ft-—— 6 ft — 5 ft- Solved Part A The compound beam is fixed at E and... Hình ảnh có thể có bản quyền. Tìm hiểu thêm Problem A-12 % Chia sẻ kip 800 lb Truy cập ) D Lưu of C 600 lb |-sa+ 10ft 5ft 4ft6ft D E 5 ft- Trying Cheaa Những kết quả này có hữu ích không? There are pins at C and D To F-1200 Egue!) Chegg Solved The compound b... Có Không ☑ ||| Chegg 10 וחarrow_forwardNo chatgpt pls will upvotearrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
University Physics Volume 3
Physics
ISBN:9781938168185
Author:William Moebs, Jeff Sanny
Publisher:OpenStax
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Glencoe Physics: Principles and Problems, Student...
Physics
ISBN:9780078807213
Author:Paul W. Zitzewitz
Publisher:Glencoe/McGraw-Hill
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Diffraction of light animation best to understand class 12 physics; Author: PTAS: Physics Tomorrow Ambition School;https://www.youtube.com/watch?v=aYkd_xSvaxE;License: Standard YouTube License, CC-BY