Chapter 3.7, Problem 5SP

Laplace Transforms

In the last few chapters, we have looked at several ways to use integration for solving real-world problems. For this next project, we are going to explore a more advanced application of integration: integral transforms. Specifically, we describe the Laplace transform and some of its properties. The Laplace transform is used in engineering and physics to simplify the computations needed to solve some problems. It takes functions expressed in terms of time and trons/orms them to functions expressed in terms of frequency. It turns out that, in many cases, the computations needed to solve problems in the frequency domain are much simpler than those required in the time domain.

The Laplace transform is defined in terms of an integral as

7

         e""

         ft

Note that the input to a Laplace transform is a function of time, /(/), and the output is a function of frequency, F(j), Although many real-world examples require the use of complex numbers (involving the imaginary number i = V—1), in this project we limit ourselves to functions of real numbers.

Let's stan with a simple example. Here we calculate the Laplace transform of /(f) = t. We have

    

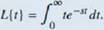
This is an improper integral, so we express it in terms of a limit, which gives

    

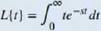
Now we use integration by pans to evaluate the integral. Note that we are integrating with respect to t, so we treat the variable s as a constant. We have

    u—t   dv    — dt

    du=dt v

  — — ye_ir.

Then we obtain

    = + +

     =    ~K + °1 -

     = Jin_L[[-i,-]-±[e--lj]

   - c  + c

    = 0-0 + -L

    s“

    _x

    2* s

1. Calculate the Laplace transform of /(/) = 1.

3.Calculate the Laplace transform of /(/) = : (Note, you will have to integrate by parts twice.)

Laplace transforms are often used to solve differential equations. Differential equations are not covered in detail until later in this book; but, for now, let’s look at the relationship between the Laplace transform of a function and the Laplace transform of its derivative.

Let’s start with the definition of the Laplace transform. We have

    WW! =    r™    r'

     = lim / e~st fifth.

4.Use integration by parts to evaluate Jjm^ e~sl fifth. (Let « = /{/) and dv — e '!dt.) After integrating by parts and evaluating the limit, you should see that

Then,

Thus, differentiation in the time domain simplifies to multiplication by s in the frequency domain.

The final thing we look at in this project is how the Laplace transforms of fit] and its antiderivative are

     related. Let g(r) — f(u}dii. Then,

     ¦'o

lim /

;-* caj"     5.Use integration by parts to evaluate hrn^y e ’ g(t)dl. (Let u = gif) and dv = e dt. Note, by the way,

that we have defined gif, du — fifth.)

As you might expect, you should see that

     L|^(r)| = |-L[/(/)i.

Integration in the time domain simplifies to division by s in ±e frequency domain.