PRECALCULUS:...COMMON CORE ED.-W/ACCESS
10th Edition
ISBN: 9780134781839
Author: Demana
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Expert Solution & Answer
Chapter 3.6, Problem 73E
Solution
a.
To find: The annual interest rate.
The annual interest rate is 8%.
Given information:
The function describes the present value of a certain annuity, where x is time in months:
Concept used:
The present value PV of an annuity consisting of n equal payments of R dollars earning an interest rate i per period (payment interval) is
Explanation:
The annual interest rate is determined by the term 0.08 i.e., 8%.
b.
To find: The number of payments per year.
There are 12 payments per year.
Given information:
The function describes the present value of a certain annuity, where x is time in months:
Concept used:
The present value PV of an annuity consisting of n equal payments of R dollars earning an interest rate i per period (payment interval) is
Explanation:
Here, in the given equation “12” determines the number of payments per year.
c.
To find: The amount of each payment.
The amount of each payment is $200.
Given information:
The function describes the present value of a certain annuity, where x is time in months:
Concept used:
The present value PV of an annuity consisting of n equal payments of R dollars earning an interest rate i per period (payment interval) is
Explanation:
On comparing the formula,
i.e., The amount of each payment is $200.
d.
To compute: The present value of the annuity paying $200 monthly after 20 years.
The present value of the annuity is $23,910.86.
Given information:
The function describes the present value of a certain annuity, where x is time in months:
Concept used:
The present value PV of an annuity consisting of n equal payments of R dollars earning an interest rate i per period (payment interval) is
Explanation:
Substitute
The present value of the annuity paying $200 monthly after 20 years is $23,910.86.
e.
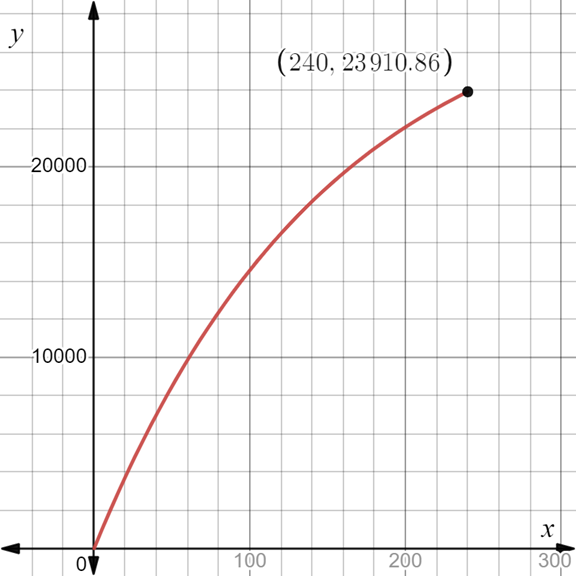
To graph: The present value function for x in the interval 0 to 20 years.
The graph of the present value function for x in the interval 0 to 20 years is shown.
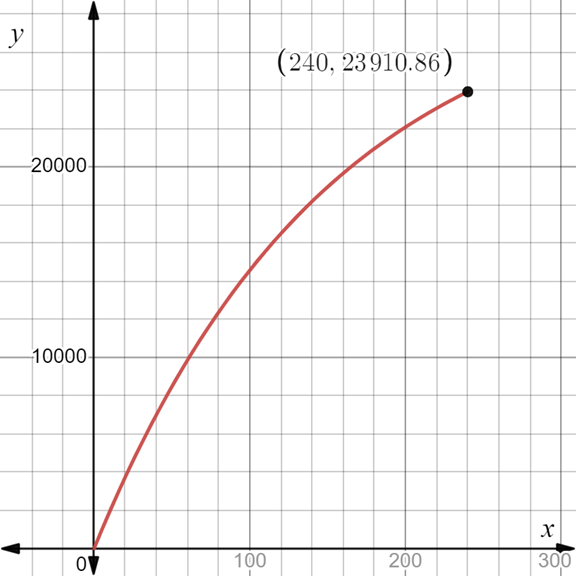
Given information:
The function describes the present value of a certain annuity, where x is time in months:
Concept used:
The present value PV of an annuity consisting of n equal payments of R dollars earning an interest rate i per period (payment interval) is
Explanation:
By using graphing calculator, plot the given expression.
f.
To explain: The amount $23,910.86 is much less than the total of all 240 monthly payments of $200, which is $4800.
$23,910.86 is the present value of the annuity paying $200 monthly after 20 years.
Its future value will be much higher than $48,000.
$23,910.86 as present value would be a better option for now.
Given information:
The function describes the present value of a certain annuity, where x is time in months:
Concept used:
The present value PV of an annuity consisting of n equal payments of R dollars earning an interest rate i per period (payment interval) is
Explanation:
$23,910.86 is the present value of the annuity paying $200 monthly after 20 years.
Its future value will be much higher than $48,000.
Thus, $23,910.86 as present value would be a better option for now.
Chapter 3 Solutions
PRECALCULUS:...COMMON CORE ED.-W/ACCESS
Ch. 3.1 - Prob. 1QRCh. 3.1 - Prob. 2QRCh. 3.1 - Prob. 3QRCh. 3.1 - Prob. 4QRCh. 3.1 - Prob. 5QRCh. 3.1 - Prob. 6QRCh. 3.1 - Prob. 7QRCh. 3.1 - Prob. 8QRCh. 3.1 - Prob. 9QRCh. 3.1 - Prob. 10QR
Ch. 3.1 - Prob. 1ECh. 3.1 - Prob. 2ECh. 3.1 - Prob. 3ECh. 3.1 - Prob. 4ECh. 3.1 - Prob. 5ECh. 3.1 - Prob. 6ECh. 3.1 - Prob. 7ECh. 3.1 - Prob. 8ECh. 3.1 - Prob. 9ECh. 3.1 - Prob. 10ECh. 3.1 - Prob. 11ECh. 3.1 - Prob. 12ECh. 3.1 - Prob. 13ECh. 3.1 - Prob. 14ECh. 3.1 - Prob. 15ECh. 3.1 - Prob. 16ECh. 3.1 - Prob. 17ECh. 3.1 - Prob. 18ECh. 3.1 - Prob. 19ECh. 3.1 - Prob. 20ECh. 3.1 - Prob. 21ECh. 3.1 - Prob. 22ECh. 3.1 - Prob. 23ECh. 3.1 - Prob. 24ECh. 3.1 - Prob. 25ECh. 3.1 - Prob. 26ECh. 3.1 - Prob. 27ECh. 3.1 - Prob. 28ECh. 3.1 - Prob. 29ECh. 3.1 - Prob. 30ECh. 3.1 - Prob. 31ECh. 3.1 - Prob. 32ECh. 3.1 - Prob. 33ECh. 3.1 - Prob. 34ECh. 3.1 - Prob. 35ECh. 3.1 - Prob. 36ECh. 3.1 - Prob. 37ECh. 3.1 - Prob. 38ECh. 3.1 - Prob. 39ECh. 3.1 - Prob. 40ECh. 3.1 - Prob. 41ECh. 3.1 - Prob. 42ECh. 3.1 - Prob. 43ECh. 3.1 - Prob. 44ECh. 3.1 - Prob. 45ECh. 3.1 - Prob. 46ECh. 3.1 - Prob. 47ECh. 3.1 - Prob. 48ECh. 3.1 - Prob. 49ECh. 3.1 - Prob. 50ECh. 3.1 - Prob. 51ECh. 3.1 - Prob. 52ECh. 3.1 - Prob. 53ECh. 3.1 - Prob. 54ECh. 3.1 - Prob. 55ECh. 3.1 - Prob. 56ECh. 3.1 - Prob. 57ECh. 3.1 - Prob. 58ECh. 3.1 - Prob. 59ECh. 3.1 - Prob. 60ECh. 3.1 - Prob. 61ECh. 3.1 - Prob. 62ECh. 3.1 - Prob. 63ECh. 3.1 - Prob. 64ECh. 3.1 - Prob. 65ECh. 3.1 - Prob. 66ECh. 3.1 - Prob. 67ECh. 3.1 - Prob. 68ECh. 3.1 - Prob. 69ECh. 3.1 - Prob. 70ECh. 3.1 - Prob. 71ECh. 3.1 - Prob. 72ECh. 3.1 - Prob. 73ECh. 3.1 - Prob. 74ECh. 3.2 - Prob. 1QRCh. 3.2 - Prob. 2QRCh. 3.2 - Prob. 3QRCh. 3.2 - Prob. 4QRCh. 3.2 - Prob. 5QRCh. 3.2 - Prob. 6QRCh. 3.2 - Prob. 7QRCh. 3.2 - Prob. 8QRCh. 3.2 - Prob. 9QRCh. 3.2 - Prob. 10QRCh. 3.2 - Prob. 1ECh. 3.2 - Prob. 2ECh. 3.2 - Prob. 3ECh. 3.2 - Prob. 4ECh. 3.2 - Prob. 5ECh. 3.2 - Prob. 6ECh. 3.2 - Prob. 7ECh. 3.2 - Prob. 8ECh. 3.2 - Prob. 9ECh. 3.2 - Prob. 10ECh. 3.2 - Prob. 11ECh. 3.2 - Prob. 12ECh. 3.2 - Prob. 13ECh. 3.2 - Prob. 14ECh. 3.2 - Prob. 15ECh. 3.2 - Prob. 16ECh. 3.2 - Prob. 17ECh. 3.2 - Prob. 18ECh. 3.2 - Prob. 19ECh. 3.2 - Prob. 20ECh. 3.2 - Prob. 21ECh. 3.2 - Prob. 22ECh. 3.2 - Prob. 23ECh. 3.2 - Prob. 24ECh. 3.2 - Prob. 25ECh. 3.2 - Prob. 26ECh. 3.2 - Prob. 27ECh. 3.2 - Prob. 28ECh. 3.2 - Prob. 29ECh. 3.2 - Prob. 30ECh. 3.2 - Prob. 31ECh. 3.2 - Prob. 32ECh. 3.2 - Prob. 33ECh. 3.2 - Prob. 34ECh. 3.2 - Prob. 35ECh. 3.2 - Prob. 36ECh. 3.2 - Prob. 37ECh. 3.2 - Prob. 38ECh. 3.2 - Prob. 39ECh. 3.2 - Prob. 40ECh. 3.2 - Prob. 41ECh. 3.2 - Prob. 42ECh. 3.2 - Prob. 43ECh. 3.2 - Prob. 44ECh. 3.2 - Prob. 45ECh. 3.2 - Prob. 46ECh. 3.2 - Prob. 47ECh. 3.2 - Prob. 48ECh. 3.2 - Prob. 49ECh. 3.2 - Prob. 50ECh. 3.2 - Prob. 51ECh. 3.2 - Prob. 52ECh. 3.2 - Prob. 53ECh. 3.2 - Prob. 54ECh. 3.2 - Prob. 55ECh. 3.2 - Prob. 56ECh. 3.2 - Prob. 57ECh. 3.2 - Prob. 58ECh. 3.2 - Prob. 59ECh. 3.2 - Prob. 60ECh. 3.2 - Prob. 61ECh. 3.3 - Prob. 1QRCh. 3.3 - Prob. 2QRCh. 3.3 - Prob. 3QRCh. 3.3 - Prob. 4QRCh. 3.3 - Prob. 5QRCh. 3.3 - Prob. 6QRCh. 3.3 - Prob. 7QRCh. 3.3 - Prob. 8QRCh. 3.3 - Prob. 9QRCh. 3.3 - Prob. 10QRCh. 3.3 - Prob. 1ECh. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - Prob. 6ECh. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - Prob. 9ECh. 3.3 - Prob. 10ECh. 3.3 - Prob. 11ECh. 3.3 - Prob. 12ECh. 3.3 - Prob. 13ECh. 3.3 - Prob. 14ECh. 3.3 - Prob. 15ECh. 3.3 - Prob. 16ECh. 3.3 - Prob. 17ECh. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Prob. 20ECh. 3.3 - Prob. 21ECh. 3.3 - Prob. 22ECh. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - Prob. 25ECh. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Prob. 29ECh. 3.3 - Prob. 30ECh. 3.3 - Prob. 31ECh. 3.3 - Prob. 32ECh. 3.3 - Prob. 33ECh. 3.3 - Prob. 34ECh. 3.3 - Prob. 35ECh. 3.3 - Prob. 36ECh. 3.3 - Prob. 37ECh. 3.3 - Prob. 38ECh. 3.3 - Prob. 39ECh. 3.3 - Prob. 40ECh. 3.3 - Prob. 41ECh. 3.3 - Prob. 42ECh. 3.3 - Prob. 43ECh. 3.3 - Prob. 44ECh. 3.3 - Prob. 45ECh. 3.3 - Prob. 46ECh. 3.3 - Prob. 47ECh. 3.3 - Prob. 48ECh. 3.3 - Prob. 49ECh. 3.3 - Prob. 50ECh. 3.3 - Prob. 51ECh. 3.3 - Prob. 52ECh. 3.3 - Prob. 53ECh. 3.3 - Prob. 54ECh. 3.3 - Prob. 55ECh. 3.3 - Prob. 56ECh. 3.3 - Prob. 57ECh. 3.3 - Prob. 58ECh. 3.3 - Prob. 59ECh. 3.3 - Prob. 60ECh. 3.3 - Prob. 61ECh. 3.3 - Prob. 62ECh. 3.3 - Prob. 63ECh. 3.3 - Prob. 64ECh. 3.3 - Prob. 65ECh. 3.3 - Prob. 66ECh. 3.3 - Prob. 67ECh. 3.3 - Prob. 68ECh. 3.3 - Prob. 69ECh. 3.3 - Prob. 70ECh. 3.3 - Prob. 71ECh. 3.3 - Prob. 72ECh. 3.3 - Prob. 73ECh. 3.3 - Prob. 74ECh. 3.3 - Prob. 75ECh. 3.4 - Prob. 1QRCh. 3.4 - Prob. 2QRCh. 3.4 - Prob. 3QRCh. 3.4 - Prob. 4QRCh. 3.4 - Prob. 5QRCh. 3.4 - Prob. 6QRCh. 3.4 - Prob. 7QRCh. 3.4 - Prob. 8QRCh. 3.4 - Prob. 9QRCh. 3.4 - Prob. 10QRCh. 3.4 - Prob. 1ECh. 3.4 - Prob. 2ECh. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - Prob. 13ECh. 3.4 - Prob. 14ECh. 3.4 - Prob. 15ECh. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Prob. 19ECh. 3.4 - Prob. 20ECh. 3.4 - Prob. 21ECh. 3.4 - Prob. 22ECh. 3.4 - Prob. 23ECh. 3.4 - Prob. 24ECh. 3.4 - Prob. 25ECh. 3.4 - Prob. 26ECh. 3.4 - Prob. 27ECh. 3.4 - Prob. 28ECh. 3.4 - Prob. 29ECh. 3.4 - Prob. 30ECh. 3.4 - Prob. 31ECh. 3.4 - Prob. 32ECh. 3.4 - Prob. 33ECh. 3.4 - Prob. 34ECh. 3.4 - Prob. 35ECh. 3.4 - Prob. 36ECh. 3.4 - Prob. 37ECh. 3.4 - Prob. 38ECh. 3.4 - Prob. 39ECh. 3.4 - Prob. 40ECh. 3.4 - Prob. 41ECh. 3.4 - Prob. 42ECh. 3.4 - Prob. 43ECh. 3.4 - Prob. 44ECh. 3.4 - Prob. 45ECh. 3.4 - Prob. 46ECh. 3.4 - Prob. 47ECh. 3.4 - Prob. 48ECh. 3.4 - Prob. 49ECh. 3.4 - Prob. 50ECh. 3.4 - Prob. 51ECh. 3.4 - Prob. 52ECh. 3.4 - Prob. 53ECh. 3.4 - Prob. 54ECh. 3.4 - Prob. 55ECh. 3.4 - Prob. 56ECh. 3.4 - Prob. 57ECh. 3.4 - Prob. 58ECh. 3.4 - Prob. 59ECh. 3.4 - Prob. 60ECh. 3.4 - Prob. 61ECh. 3.4 - Prob. 62ECh. 3.4 - Prob. 63ECh. 3.4 - Prob. 64ECh. 3.4 - Prob. 65ECh. 3.4 - Prob. 66ECh. 3.4 - Prob. 67ECh. 3.4 - Prob. 68ECh. 3.4 - Prob. 69ECh. 3.4 - Prob. 70ECh. 3.4 - Prob. 71ECh. 3.4 - Prob. 72ECh. 3.4 - Prob. 73ECh. 3.5 - Prob. 1QRCh. 3.5 - Prob. 2QRCh. 3.5 - Prob. 3QRCh. 3.5 - Prob. 4QRCh. 3.5 - Prob. 5QRCh. 3.5 - Prob. 6QRCh. 3.5 - Prob. 7QRCh. 3.5 - Prob. 8QRCh. 3.5 - Prob. 9QRCh. 3.5 - Prob. 10QRCh. 3.5 - Prob. 1ECh. 3.5 - Prob. 2ECh. 3.5 - Prob. 3ECh. 3.5 - Prob. 4ECh. 3.5 - Prob. 5ECh. 3.5 - Prob. 6ECh. 3.5 - Prob. 7ECh. 3.5 - Prob. 8ECh. 3.5 - Prob. 9ECh. 3.5 - Prob. 10ECh. 3.5 - Prob. 11ECh. 3.5 - Prob. 12ECh. 3.5 - Prob. 13ECh. 3.5 - Prob. 14ECh. 3.5 - Prob. 15ECh. 3.5 - Prob. 16ECh. 3.5 - Prob. 17ECh. 3.5 - Prob. 18ECh. 3.5 - Prob. 19ECh. 3.5 - Prob. 20ECh. 3.5 - Prob. 21ECh. 3.5 - Prob. 22ECh. 3.5 - Prob. 23ECh. 3.5 - Prob. 24ECh. 3.5 - Prob. 25ECh. 3.5 - Prob. 26ECh. 3.5 - Prob. 27ECh. 3.5 - Prob. 28ECh. 3.5 - Prob. 29ECh. 3.5 - Prob. 30ECh. 3.5 - Prob. 31ECh. 3.5 - Prob. 32ECh. 3.5 - Prob. 33ECh. 3.5 - Prob. 34ECh. 3.5 - Prob. 35ECh. 3.5 - Prob. 36ECh. 3.5 - Prob. 37ECh. 3.5 - Prob. 38ECh. 3.5 - Prob. 39ECh. 3.5 - Prob. 40ECh. 3.5 - Prob. 41ECh. 3.5 - Prob. 42ECh. 3.5 - Prob. 43ECh. 3.5 - Prob. 44ECh. 3.5 - Prob. 45ECh. 3.5 - Prob. 46ECh. 3.5 - Prob. 47ECh. 3.5 - Prob. 48ECh. 3.5 - Prob. 49ECh. 3.5 - Prob. 50ECh. 3.5 - Prob. 51ECh. 3.5 - Prob. 52ECh. 3.5 - Prob. 53ECh. 3.5 - Prob. 54ECh. 3.5 - Prob. 55ECh. 3.5 - Prob. 56ECh. 3.5 - Prob. 57ECh. 3.5 - Prob. 58ECh. 3.5 - Prob. 59ECh. 3.5 - Prob. 60ECh. 3.5 - Prob. 61ECh. 3.5 - Prob. 62ECh. 3.5 - Prob. 63ECh. 3.5 - Prob. 64ECh. 3.5 - Prob. 65ECh. 3.5 - Prob. 66ECh. 3.5 - Prob. 67ECh. 3.5 - Prob. 68ECh. 3.5 - Prob. 69ECh. 3.5 - Prob. 70ECh. 3.5 - Prob. 71ECh. 3.5 - Prob. 72ECh. 3.5 - Prob. 73ECh. 3.5 - Prob. 74ECh. 3.5 - Prob. 75ECh. 3.5 - Prob. 76ECh. 3.5 - Prob. 77ECh. 3.5 - Prob. 78ECh. 3.5 - Prob. 79ECh. 3.6 - Prob. 1QRCh. 3.6 - Prob. 2QRCh. 3.6 - Prob. 3QRCh. 3.6 - Prob. 4QRCh. 3.6 - Prob. 5QRCh. 3.6 - Prob. 6QRCh. 3.6 - Prob. 7QRCh. 3.6 - Prob. 8QRCh. 3.6 - Prob. 9QRCh. 3.6 - Prob. 10QRCh. 3.6 - Prob. 1ECh. 3.6 - Prob. 2ECh. 3.6 - Prob. 3ECh. 3.6 - Prob. 4ECh. 3.6 - Prob. 5ECh. 3.6 - Prob. 6ECh. 3.6 - Prob. 7ECh. 3.6 - Prob. 8ECh. 3.6 - Prob. 9ECh. 3.6 - Prob. 10ECh. 3.6 - Prob. 11ECh. 3.6 - Prob. 12ECh. 3.6 - Prob. 13ECh. 3.6 - Prob. 14ECh. 3.6 - Prob. 15ECh. 3.6 - Prob. 16ECh. 3.6 - Prob. 17ECh. 3.6 - Prob. 18ECh. 3.6 - Prob. 19ECh. 3.6 - Prob. 20ECh. 3.6 - Prob. 21ECh. 3.6 - Prob. 22ECh. 3.6 - Prob. 23ECh. 3.6 - Prob. 24ECh. 3.6 - Prob. 25ECh. 3.6 - Prob. 26ECh. 3.6 - Prob. 27ECh. 3.6 - Prob. 28ECh. 3.6 - Prob. 29ECh. 3.6 - Prob. 30ECh. 3.6 - Prob. 31ECh. 3.6 - Prob. 32ECh. 3.6 - Prob. 33ECh. 3.6 - Prob. 34ECh. 3.6 - Prob. 35ECh. 3.6 - Prob. 36ECh. 3.6 - Prob. 37ECh. 3.6 - Prob. 38ECh. 3.6 - Prob. 39ECh. 3.6 - Prob. 40ECh. 3.6 - Prob. 41ECh. 3.6 - Prob. 42ECh. 3.6 - Prob. 43ECh. 3.6 - Prob. 44ECh. 3.6 - Prob. 45ECh. 3.6 - Prob. 46ECh. 3.6 - Prob. 47ECh. 3.6 - Prob. 48ECh. 3.6 - Prob. 49ECh. 3.6 - Prob. 50ECh. 3.6 - Prob. 51ECh. 3.6 - Prob. 52ECh. 3.6 - Prob. 53ECh. 3.6 - Prob. 54ECh. 3.6 - Prob. 55ECh. 3.6 - Prob. 56ECh. 3.6 - Prob. 57ECh. 3.6 - Prob. 58ECh. 3.6 - Prob. 59ECh. 3.6 - Prob. 60ECh. 3.6 - Prob. 61ECh. 3.6 - Prob. 62ECh. 3.6 - Prob. 63ECh. 3.6 - Prob. 64ECh. 3.6 - Prob. 65ECh. 3.6 - Prob. 66ECh. 3.6 - Prob. 67ECh. 3.6 - Prob. 68ECh. 3.6 - Prob. 69ECh. 3.6 - Prob. 70ECh. 3.6 - Prob. 71ECh. 3.6 - Prob. 72ECh. 3.6 - Prob. 73ECh. 3 - Prob. 1RECh. 3 - Prob. 2RECh. 3 - Prob. 3RECh. 3 - Prob. 4RECh. 3 - Prob. 5RECh. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Prob. 8RECh. 3 - Prob. 9RECh. 3 - Prob. 10RECh. 3 - Prob. 11RECh. 3 - Prob. 12RECh. 3 - Prob. 13RECh. 3 - Prob. 14RECh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Prob. 21RECh. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - Prob. 24RECh. 3 - Prob. 25RECh. 3 - Prob. 26RECh. 3 - Prob. 27RECh. 3 - Prob. 28RECh. 3 - Prob. 29RECh. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Prob. 33RECh. 3 - Prob. 34RECh. 3 - Prob. 35RECh. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Prob. 38RECh. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Prob. 45RECh. 3 - Prob. 46RECh. 3 - Prob. 47RECh. 3 - Prob. 48RECh. 3 - Prob. 49RECh. 3 - Prob. 50RECh. 3 - Prob. 51RECh. 3 - Prob. 52RECh. 3 - Prob. 53RECh. 3 - Prob. 54RECh. 3 - Prob. 55RECh. 3 - Prob. 56RECh. 3 - Prob. 57RECh. 3 - Prob. 58RECh. 3 - Prob. 59RECh. 3 - Prob. 60RECh. 3 - Prob. 61RECh. 3 - Prob. 62RECh. 3 - Prob. 63RECh. 3 - Prob. 64RECh. 3 - Prob. 65RECh. 3 - Prob. 66RECh. 3 - Prob. 67RECh. 3 - Prob. 68RECh. 3 - Prob. 69RECh. 3 - Prob. 70RECh. 3 - Prob. 71RECh. 3 - Prob. 72RECh. 3 - Prob. 73RECh. 3 - Prob. 74RECh. 3 - Prob. 75RECh. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - Prob. 78RECh. 3 - Prob. 79RECh. 3 - Prob. 80RECh. 3 - Prob. 81RECh. 3 - Prob. 82RECh. 3 - Prob. 83RECh. 3 - Prob. 84RECh. 3 - Prob. 85RECh. 3 - Prob. 86RECh. 3 - Prob. 87RECh. 3 - Prob. 88RECh. 3 - Prob. 89RECh. 3 - Prob. 90RECh. 3 - Prob. 91RECh. 3 - Prob. 92RECh. 3 - Prob. 93RECh. 3 - Prob. 94RECh. 3 - Prob. 95RECh. 3 - Prob. 96RECh. 3 - Prob. 97RECh. 3 - Prob. 98RECh. 3 - Prob. 99RE
Knowledge Booster
Similar questions
- Consider the graphs of y = f(x) and y = g(x) in the given diagram y= f(x). y = g(x) Evaluate (f+g)(2) -5 Determine all for which g(x) < f(x) Determine all for which f(x) +3 = g(x)arrow_forwardI) For what value(s) of x does g(x) = -4? Separate multiple answers with commas as needed. J) Give the interval(s) of such that g(x) > 0. Use the union symbol between multiple intervals. K) Give the interval(s) of such that g(x) <0. Use the union symbol between multiple intervals.arrow_forwardneed help on Barrow_forward
- 4. Use the properties of limits to help decide whether each limit exists. If a limit exists, fi lim (2x²-4x+5) a) x-4 b) lim 2 x²-16 x-4x+2x-8arrow_forward7. The concentration of a drug in a patient's bloodstream h hours after it was injected is given by 0.17 h Ah= h²+2' Find and interpret lim A(h). Remember, the answers to word problems should always be given in a complete h→00 sentence, with proper units, in the context of the problem.arrow_forward#2arrow_forward
- 2. We want to find the inverse of f(x) = (x+3)² a. On the graph at right, sketch f(x). (Hint: use what you know about transformations!) (2 points) b. What domain should we choose to get only the part of f (x) that is one- to-one and non-decreasing? Give your answer in inequality notation. (2 points) - c. Now use algebra to find f¯¹ (x). (2 points) -4- 3- 2 1 -4 -3 -2 -1 0 1 -1- -2- --3- -4 -N- 2 3 4arrow_forward1. Suppose f(x) = 2 4 == x+3 and g(x) = ½-½. Find and fully simplify ƒ(g(x)). Be sure to show all x your work, write neatly so your work is easy to follow, and connect your expressions with equals signs. (4 points)arrow_forwardFind the ane sided limit lim 2 x+1-3x-3arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning