
Concept explainers
Figure P36.95 shows a thin converging lens for which the radii of curvature of its surfaces have magnitudes of 9.00 cm and 11.0 cm. The lens is in front of a concave spherical mirror with the radius of curvature R = 8.00 cm. Assume the focal points F1 and F2 of the lens are 5.00 cm from the center of the lens, (a) Determine the index of refraction of the lens material. The lens and mirror are 20.0 cm apart, and an object is placed 8.00 cm to the left of the lens. Determine (b) the position of the filial image and (c) its magnification as seen by the eye in the figure. (d) Is the final image inverted or upright? Explain.
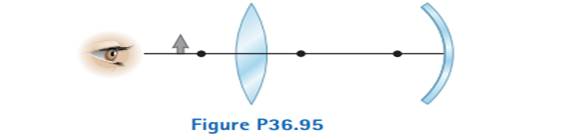
(a)
The index of refraction of the lens material.
Answer to Problem 36.95CP
The index of refraction of the lens material is
Explanation of Solution
Given data: The radii of curvature for the converging Len’s surfaces are
Write the expression for the focal length of the lens,
Here,
Substitute
Conclusion:
Therefore the index of refraction of the lens material is
(b)
The position of the final image.
Answer to Problem 36.95CP
The position of the final image is
Explanation of Solution
Given data: The radii of curvature for the converging Len’s surfaces are
The expression for the focal length is,
Here,
Substitute
Thus the focal length is
The expression for the lens equation is,
Here,
Substitute
Thus the image distance from the lens is
The expression for the object distance for mirror is,
Here,
Substitute
Thus the object distance for mirror is
The expression for the mirror equation is,
Here,
Substitute
Thus the image distance from the mirror is
The expression for the object distance for lens is,
Substitute
Thus the object distance for lens is
The expression for the lens equation is,
Here,
Substitute
Conclusion:
Therefore the position of the final image is
(c)
The magnification as seen by the eye in the figure.
Answer to Problem 36.95CP
The magnification as seen by the eye in the figure is
Explanation of Solution
Given data: The radii of curvature for the converging Len’s surfaces are
The overall magnification factor is,
Substitute
Conclusion:
Therefore the magnification as seen by the eye in the figure is
(d)
Whether the final image is inverted or upright.
Answer to Problem 36.95CP
The final image is inverted.
Explanation of Solution
Given data: The radii of curvature for the converging Len’s surfaces are
From part (c) of the question the value of the magnification factor is,
It is known that the image will be upright when the magnification factor is positive and the image will be inverted when the magnification factor is negative.
Since the magnification factor is negative so the image will be upright.
Conclusion:
Therefore the final image is inverted.
Want to see more full solutions like this?
Chapter 36 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- Why is the following situation impossible? Consider the lensmirror combination shown in Figure P35.55. The lens has a focal length of fL = 0.200 m, and the mirror has a focal length of fM = 0.500 m. The lens and mirror are placed a distance d = 1.30 m apart, and an object is placed at p = 0.300 m from the lens. By moving a screen to various positions to the left of the lens, a student finds two different positions of the screen that produce a sharp image of the object. One of these positions corresponds to light leaving the object and traveling to the left through the lens. The other position corresponds to light traveling to the right from the object, reflecting from the mirror and then passing through the lens. Figure P35.55 Problem 55 and 57.arrow_forwardFigure P38.43 shows a concave meniscus lens. If |r1| = 8.50 cm and |r2| = 6.50 cm, find the focal length and determine whether the lens is converging or diverging. The lens is made of glass with index of refraction n = 1.55. CHECK and THINK: How do your answers change if the object is placed on the right side of the lens? FIGURE P38.43arrow_forwardThe left face of a biconvex lens has a radius of curvature of magnitude 12.0 cm, and the right face has a radius of curvature of magnitude 18.0 cm. The index of refraction of the glass is 1.44. (a) Calculate the focal length of the lens for light incident from the left. (b) What If? After the lens is turned around to interchange the radii of curvature of the two faces, calculate the focal length of the lens for light incident from the left.arrow_forward
- Figure P26.72 shows a thin converging lens for which the radii of curvature of its surfaces have magnitudes of 9.00 cm and 11.0 cm. The lens is in front of a concave spherical mirror with the radius of curvature R = 8.00 cm. Assume the focal points F1 and F2 of the lens are 5.00 cm from the center of the lens. (a) Determine the index of refraction of the lens material. The lens and mirror are 20.0 cm apart, and an object is placed 8.00 cm to the left of the lens. Determine (b) the position of the final image and (c) its magnification as seen by the eye in the figure. (d) Is the final image inverted or upright? Explain.arrow_forwardA converging lens made of crown glass has a focal length of 15.0 cm when used in air. If the lens is immersed in water, what is its focal length? (a) negative (b) less than 15.0 cm (c) equal to 15.0 cm (d) greater than 15.0 cm (e) none of those answersarrow_forwardIn Figure P26.38, a thin converging lens of focal length 14.0 cm forms an image of the square abcd, which is hc = hb = 10.0 cm high and lies between distances of pd = 20.0 cm and pa = 30.0 cm from the lens. Let a, b, c, and d represent the respective corners of the image. Let qa represent the image distance for points a and b, qd represent the image distance for points c and d, hb represent the distance from point b to the axis, and hc represent the height of c. (a) Find qa, qd, hb, and hc. (b) Make a sketch of the image. (c) The area of the object is 100 cm2. By carrying out the following steps, you will evaluate the area of the image. Let q represent the image distance of any point between a and d, for which the object distance is p. Let h represent the distance from the axis to the point at the edge of the image between b and c at image distance q. Demonstrate that h=10.0q(114.01q) where h and q are in centimeters. (d) Explain why the geometric area of the image is given by qaqdhdq (e) Carry out the integration to find the area of the image. Figure P26.38arrow_forward
- A floating strawberry illusion is achieved with two parabolic mirrors, each having a focal length 7.50 cm, facing each other as shown in Figure P33.58. If a strawberry is placed on the lower mirror, an image of the strawberry is formed at the small opening at the center of the top mirror, 7.50 cm above the lowest point of the bottom mirror. The position of the eye in Figure P35.58a corresponds to the view of the apparatus in Figure P35.58b. Consider the light path marked A. Notice that this light path is blocked by the upper mirror so that the strawberry itself is not directly observable. The light path marked B corresponds to the eye viewing the image of the strawberry that is formed at the opening at the top of the apparatus. (a) Show that the final image is formed at that location and describe its characteristics. (b) A very startling effect is to shine a flashlight beam on this image. Even al a glancing angle, the incoming light beam is seemingly reflected from the image! Explain. Figure P35.58arrow_forwardAn observer to the right of the mirror-lens combination shown in Figure P36.89 (not to scale) sees two real images that are the same size and in the same location. One image is upright, and the other is inverted. Both images are 1.50 times larger than the object. The lens has a focal length of 10.0 cm. The lens and mirror are separated by 40.0 cm. Determine the focal length of the mirror.arrow_forwardA lamp of height S cm is placed 40 cm in front of a converging lens of focal length 20 cm. There is a plane mirror 15 cm behind the lens. Where would you find the image when you look in the mirror?arrow_forward
- How many times will the incident beam in Figure P34.33 (page 922) be reflected by each of the parallel mirrors? Figure P34.33arrow_forwardWhat will be the formula for the angular magnification of a convex lens of focal length f if the eye is very close to the lens and the near point is located a distance D from the eye?arrow_forwardThe figure below shows a thin converging lens for which the radii of curvature of its surfaces have magnitudes of 8.90 cm and 10.4 cm. The lens is in front of a concave spherical mirror with the radius of curvature R = 8.38 cm. Assume the focal points F₁ and F₂ of the lens are 5.00 cm from the center of the lens. :) (a) Determine the index of refraction of the lens material.arrow_forward
 Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





