STATISTICS F/BUSINESS+ECONOMICS-TEXT
13th Edition
ISBN: 9781305881884
Author: Anderson
Publisher: CENGAGE L
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
thumb_up100%
Chapter 3.5, Problem 57E
Ten major college football bowl games were played in January 2010, with the University of Alabama beating the University of Texas 37 to 21 to become the national champion of college football. The results of the 10 bowl games follow (USA today, January 8, 2010).
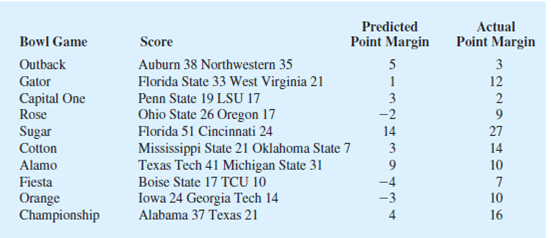
The predicted winning point margin was based on Las Vegas betting odds approximately one week before the bowl games were played. For example, Auburn was predicted to beat Northwestern in the Outback Bowl by five points. The actual winning point margin for Auburn was three points. A negative predicted winning point margin means that the team that won the bowl game was an underdog and expected to lose. For example, in the Rose Bowl, Ohio State was a two-point underdog to Oregon and ended up winning by nine points.
- a. Develop a
scatter diagram with predicted point margin on the horizontal axis. - b. What is the relationship between predicted and actual point margins?
- c. Compute and interpret the sample
covariance . - d. Compute the sample
correlation coefficient . What does this value indicate about the relationship between the Las Vegas predicted point margin and the actual point margin in college football bowl games?
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Several states have an annual raffle called the Millionare Raffle. A ticket with a unique 6-digit number cost $20 and if the numbers on your ticket are matched, you can win a prize. There are 4 prizes worth $1 million and 12 prizes of $100,000. Suppose only 125,000 tickets are sold. What are your expected winnings?
The two finalists in a tennis tournament are playing for the championship. The winner will receive $60,000 and the runner-up $35,000. Determine the expected winnings for each participant if the players are considered to be evenly matched. What would the expected winnings be if one player were favored by 4-to-1 odds?
A technology store holds a contest to attract shoppers.
works: An ace and four other cards are shuffled and placed face down on a table. The customer gets to turn over cards one at a time, looking for the ace.
The person wins $100 of store credit if the ace is the first card, $50 if it is the second card, and $20, $10, or $5 if it is the third, fourth, or last card chosen.
What is the average dollar amount of store credit given away in the contest? Estimate with a simulation of 10 trials.
Once an hour, someone at checkout is chosen at random to play in the contest Here's how it
67819
00354
91439
91073
49258
15992
41277
75111
67496
68430
09875
08990
27656
15871
23637
00952
97818
64234
50199
05715
Chapter 3 Solutions
STATISTICS F/BUSINESS+ECONOMICS-TEXT
Ch. 3.1 - Consider a sample with data values of 10, 20, 12,...Ch. 3.1 - Consider a sample with data values of 10, 20, 21,...Ch. 3.1 - Consider the following data and corresponding...Ch. 3.1 - Consider the following data. Period Rate of Return...Ch. 3.1 - Consider a sample with data values of 27, 25, 20,...Ch. 3.1 - Consider a sample with data values of 53, 55, 70,...Ch. 3.1 - The average number of minutes Americans commute to...Ch. 3.1 - The Wall Street Journal reported that the median...Ch. 3.1 - Which companies spend the most money on...Ch. 3.1 - Over a nine-month period, OutdoorGearLab tested...
Ch. 3.1 - According to the National Education Association...Ch. 3.1 - The Big Bang Theory, a situation comedy featuring...Ch. 3.1 - In automobile mileage and gasoline-consumption...Ch. 3.1 - The data contained in the file named StateUnemp...Ch. 3.1 - Martinez Auto Supplies has retail stores located...Ch. 3.1 - The grade point average for college students is...Ch. 3.1 - The following table shows the total return and the...Ch. 3.1 - Based on a survey of masters programs in business...Ch. 3.1 - Annual revenue for Corning Supplies grew by 5.5%...Ch. 3.1 - Suppose that at the beginning of 2004 you invested...Ch. 3.1 - If an asset declines in value from 5000 to 3500...Ch. 3.1 - The current value of a company is 25 million. If...Ch. 3.2 - Consider a sample with data values of 10, 20, 12,...Ch. 3.2 - Consider a sample with data values of 10, 20, 12,...Ch. 3.2 - Consider a sample with data values of 27, 25, 20,...Ch. 3.2 - Data collected by the Oil Price information...Ch. 3.2 - The results of a search to find the least...Ch. 3.2 - The Australian Open is the first of the four grand...Ch. 3.2 - The Los Angeles times regularly reports the air...Ch. 3.2 - The following data were used to construct the...Ch. 3.2 - The results of Accounting Principals latest...Ch. 3.2 - Advertising age annually compiles a list of the...Ch. 3.2 - Scores turned in by an amateur golfer at the...Ch. 3.2 - The following times were recorded by the...Ch. 3.3 - Consider a sample with data values of 10, 20, 12,...Ch. 3.3 - Consider a sample with a mean of 500 and a...Ch. 3.3 - Consider a sample with a mean of 30 and a standard...Ch. 3.3 - Suppose the data have a bell-shaped distribution...Ch. 3.3 - The results of a national survey showed that on...Ch. 3.3 - The energy information Administration reported...Ch. 3.3 - The Graduate Management Admission Test (GMAT) is a...Ch. 3.3 - Many families in California are using backyard...Ch. 3.3 - According to a Los Angeles Times study of more...Ch. 3.3 - A sample of 10 NCAA college basketball game scores...Ch. 3.3 - The Wall Street Journal reported that Walmart...Ch. 3.4 - Consider a sample with data values of 27, 25, 20,...Ch. 3.4 - Prob. 47ECh. 3.4 - Prob. 48ECh. 3.4 - A data set has a first quartile of 42 and a third...Ch. 3.4 - Naples, Florida, hosts a half-marathon (13.1-mile...Ch. 3.4 - Annual sales, in millions of dollars, for 21...Ch. 3.4 - Consumer Reports provided overall customer...Ch. 3.4 - Fortune magazines list of the worlds most admired...Ch. 3.4 - The Bureau of Transportation Statistics keeps...Ch. 3.5 - Five observations taken for two variables follow....Ch. 3.5 - Five observations taken for two variables follow....Ch. 3.5 - Ten major college football bowl games were played...Ch. 3.5 - A department of transportations study on driving...Ch. 3.5 - Over the past 40 years, the percentage of homes in...Ch. 3.5 - The Russell 1000 is a stock market index...Ch. 3.5 - A random sample of 30 colleges from Kiplingers...Ch. 3 - The average number of times Americans dine out in...Ch. 3 - USA Today reports that NCAA colleges and...Ch. 3 - The average waiting time for a patient at an El...Ch. 3 - U.S. companies lose 63.2 billion per year from...Ch. 3 - A study of smartphone users shows that 68% of...Ch. 3 - Public transportation and the automobile are two...Ch. 3 - In 2007 the New York Times reported that the...Ch. 3 - The data contained in the DATAfile named...Ch. 3 - Travel + Leisure magazine provides an annual list...Ch. 3 - The 32 teams in the National Football League (NFL)...Ch. 3 - Does a major league baseball teams record during...Ch. 3 - The days to maturity for a sample of five money...Ch. 3 - Automobiles traveling on a road with a posted...Ch. 3 - The Panama Railroad Company was established in...Ch. 3 - Pelican Stores Pelican Stores, a division of...Ch. 3 - Motion Picture Industry The motion picture...Ch. 3 - Business Schools of Asia-Pacific The pursuit of a...Ch. 3 - African Elephant Populations Although millions of...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- In the Olympic finals, only three teams are represented: US, England and China. Tatjana believes the US will win and offers even odds of 1:1. Tyler is supporting England and is offering 2:1 odds. Finally, Jeff supports China as given by 5:4 odds. Determine the optimal way of dividing $100 to bet that ensures the largest winning.arrow_forwardA roulette wheel has 38 slots, numbered 0, 00, and 1 to 36. The slots 0 and 00 are colored green, 18 of the others are red, and 18 are black. The dealer spins the wheel and, at the same time, rolls a small ball along the wheel in the opposite direction. The wheel is carefully balanced so that the ball is equally likely to land in any slot when the wheel slows. Gamblers can bet on various combinations of numbers and colors. bo(c) If you bet the same amount on each play and win on exactly 4 of the 8 plays, you will "break even." What is the probability that you will break even? Give your answer to five decimal places. O Macmillan Learning P(X = 4) =arrow_forwardA roulette wheel has 38 slots, numbered 0, 00, and 1 to 36. The slots 0 and 00 are colored green, 18 of the others are red, and 18 are black. The dealer spins the wheel and, at the same time, rolls a small ball along the wheel in the opposite direction. The wheel is carefully balanced so that the ball is equally likely to land in any slot when the wheel slows. Gamblers can bet on various combinations of numbers and colors. A) What is the probability of any one of the 38 possible outcomes? Explain your answer. B) If you bet on “red,” you win if the ball lands in a red slot. What is the probability of winning? C) A friend tells you that the odds that a bet on “red” will win are 10 to 9. Is your friend correct? If not, what are the correct odds? D The slot numbers are laid out on a board on which gamblers place their bets. One column of numbers on the board contains all multiples of 3, that is, 3, 6, 9, … , 36. You place a “column bet” that wins if any of these numbers comes up. What is…arrow_forward
- A roulette wheel has 38 slots, numbered 0, 00, and 1 to 36. The slots 0 and 00 are colored green, 18 of the others are red, and 18 are black. The dealer spins the wheel and, at the same time, rolls a small ball along the wheel in the opposite direction. The wheel is carefully balanced so that the ball is equally likely to land in any slot when the wheel slows. Gamblers can bet on various combinations of numbers and colors. What is the probability of any one of the 38 possible outcomes to three decimal places? probability: M O hp 18 L f9 D) fo Bo 43°F Clear 12 num ik 6:39 PM 11/26/2022 insert 1arrow_forwardYou pay $20 to enter a raffle. The first ticket drawn wins $990, the second ticket drawn wins $465, the third through fifth win $203, and the sixth through tenth win $49. Suppose 2032 tickets were sold. What is the expected earning on your ticket?arrow_forwardA roulette wheel has 38 numbers, with 18 odd numbers (black) and 18 even numbers(red), as well as 0 and 00 (which are green). You bet 5 dollars that the outcome is anodd number. If you win you get 10 dollars; otherwise you lose your 5 dollars. Note:assume the 0 and 00 numbers are considered even numbers What is your expected winnings? Which of these options is best: bet on an odd number or don’t bet? Why?arrow_forward
- In roulette, the numbers from 1 to 36 are evenly distributed between red and black. A player who bets $1 on black wins $1 (and gets the $1 bet back) if the ball comes to rest on black; otherwise (if the ball lands on red, 0, or 00), the $1 bet is lost. One option in a roulette game is to bet $8 on red. If the ball lands on red, you get to keep the $8 you paid to play the game, and you are awarded $9. If the ball lands elsewhere, you are awarded nothing, and the $8 that you bet is collected. What is the expected value of the game?arrow_forwardIn roulette, the numbers from 1 to 36 are evenly distributed between red and black. A player who bets $1 on black wins $1 (and gets the $1 bet back) if the ball comes to rest on black; otherwise (if the ball lands on red, 0, or 00), the $1 bet is lost. One option in a roulette game is to bet $17 on red. If the ball lands on red, you get to keep the $17 you paid to play the game, and you are awarded $19. If the ball lands elsewhere, you are awarded nothing, and the $17 that you bet is collected. What is the expected value of the game The expected value for playing roulette if you bet $17 on red is approximatelyarrow_forwardIn roulette, the numbers from 1 to 36 are evenly distributed between red and black. A player who bets $1 on black wins $1 (and gets the $1 bet back) if the ball comes to rest on black; otherwise (if the ball lands on red, 0, or 00), the $1 bet is lost. One option in a roulette game is to bet $19 on red. If the ball lands on red, you get to keep the $19 you paid to play the game, and you are awarded $21. If the ball lands elsewhere, you are awarded nothing, and the $19 that you bet is collected. What is the expected value of the game? The expected value for playing roulette if you bet $19 on red is approximately $ (Round to the nearest cent as needed.)arrow_forward
- A roulette wheel has 38 slots, numbered 0, 00, and 1 to 36. The slots 0 and 00 are colored green, 18 of the others are red, and 18 are black. The dealer spins the wheel and at the same time rolls a small ball along the wheel in the opposite direction. The wheel is carefully balanced so that the ball is equally likely to land in any slot when the wheel slows. Gamblers can bet on various combinations of numbers and colors. (Round your answers to four decimal places.) (a) If you bet on "red," you win if the ball lands in a red slot. What is the probability of winning with a bet on red in a single play of roulette?(b) You decide to play roulette four times, each time betting on red. What is the distribution of X, the number of times you win? normal distribution with ? = 4 and ? ≈ 0.5263 binomial distribution with n = 4 and p ≈ 0.4737 binomial distribution, with n = 4 and p ≈ 0.5263 binomial distribution, with n = 4 and p = 1/38 normal distribution with ? = 4 and ? ≈ 0.4737 (c) If you…arrow_forwardThe new england patriorts and the dallas cowboys are playing. what are the possible outcomesarrow_forwardMany casinos have a game called the Big Six Money Wheel, which has 54 slots in which are displayed a Joker, the casino logo, and various dollar amounts, as shown in the table below. Players may bet on the Joker, the casino logo, or one or more dollar denominations. The wheel is spun and if the wheel stops on the same place as the player's bet, the player wins that amount for each dollar bet. Suppose a player bets $25 on the Joker denomination. What is the probability of winning this bet? (Write your answer as a fraction.) The (simplified) probability of winning this bet is 1/54.What is the probability of losing this bet? (Write your answer as a fraction.) The (simplified) probability of losing this bet is 53/54.If a player bets $25 on the Joker denomination, find the player's expectation. (Round your answer to two decimal places.)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
The Fundamental Counting Principle; Author: AlRichards314;https://www.youtube.com/watch?v=549eLWIu0Xk;License: Standard YouTube License, CC-BY
The Counting Principle; Author: Mathispower4u;https://www.youtube.com/watch?v=qJ7AYDmHVRE;License: Standard YouTube License, CC-BY