BIG IDEAS MATH Integrated Math 1: Student Edition 2016
16th Edition
ISBN: 9781680331127
Author: HOUGHTON MIFFLIN HARCOURT
Publisher: Houghton Mifflin Harcourt
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 3.5, Problem 42E
(a)
To determine
To find: the shapes of line form by the graph with explanation.
(a)
Expert Solution
Answer to Problem 42E
It formed a trapezoid, which is a quadrilateral with no side parallel.
Explanation of Solution
Given:
Concept used:
Graph can be draw using graphing calculator like Desmos graphing calculator.
The straight lines form an intersection with one another or it is parallel to each other.
Calculation:
The functions are
The graph of the functions is:
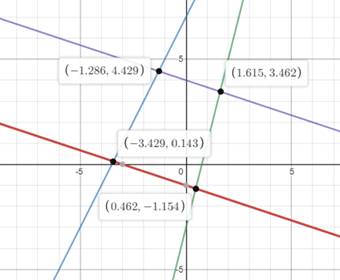
Hence, the shape formed a trapezoid, which is a quadrilateral with no side parallel.
(b)
To determine
To find: the conjecture about the equations of parallel lines.
(b)
Expert Solution
Answer to Problem 42E
In the case the two parallel lines are
Explanation of Solution
Given:
Concept used:
Conjecture angle
Then the two lines are parallel to each other.
Calculation:
The conjecture is angle
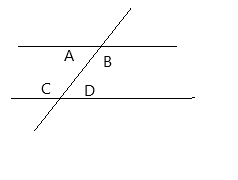
Hence, In the case the two parallel lines are
Chapter 3 Solutions
BIG IDEAS MATH Integrated Math 1: Student Edition 2016
Ch. 3.1 - Prob. 1ECh. 3.1 - Prob. 2ECh. 3.1 - Prob. 3ECh. 3.1 - Prob. 4ECh. 3.1 - Prob. 5ECh. 3.1 - Prob. 6ECh. 3.1 - Prob. 7ECh. 3.1 - Prob. 8ECh. 3.1 - Prob. 9ECh. 3.1 - Prob. 10E
Ch. 3.1 - Prob. 11ECh. 3.1 - Prob. 12ECh. 3.1 - Prob. 13ECh. 3.1 - Prob. 14ECh. 3.1 - Prob. 15ECh. 3.1 - Prob. 16ECh. 3.1 - Prob. 17ECh. 3.1 - Prob. 18ECh. 3.1 - Prob. 19ECh. 3.1 - Prob. 20ECh. 3.1 - Prob. 21ECh. 3.1 - Prob. 22ECh. 3.1 - Prob. 23ECh. 3.1 - Prob. 24ECh. 3.1 - Prob. 25ECh. 3.1 - Prob. 26ECh. 3.1 - Prob. 27ECh. 3.1 - Prob. 28ECh. 3.1 - Prob. 29ECh. 3.1 - Prob. 30ECh. 3.1 - Prob. 31ECh. 3.1 - Prob. 32ECh. 3.1 - Prob. 33ECh. 3.1 - Prob. 34ECh. 3.1 - Prob. 35ECh. 3.1 - Prob. 36ECh. 3.1 - Prob. 37ECh. 3.1 - Prob. 38ECh. 3.1 - Prob. 39ECh. 3.1 - Prob. 40ECh. 3.1 - Prob. 41ECh. 3.1 - Prob. 42ECh. 3.1 - Prob. 43ECh. 3.1 - Prob. 44ECh. 3.1 - Prob. 45ECh. 3.1 - Prob. 46ECh. 3.1 - Prob. 47ECh. 3.1 - Prob. 48ECh. 3.1 - Prob. 49ECh. 3.1 - Prob. 50ECh. 3.1 - Prob. 51ECh. 3.2 - Prob. 1ECh. 3.2 - Prob. 2ECh. 3.2 - Prob. 3ECh. 3.2 - Prob. 4ECh. 3.2 - Prob. 5ECh. 3.2 - Prob. 6ECh. 3.2 - Prob. 7ECh. 3.2 - Prob. 8ECh. 3.2 - Prob. 9ECh. 3.2 - Prob. 10ECh. 3.2 - Prob. 11ECh. 3.2 - Prob. 12ECh. 3.2 - Prob. 13ECh. 3.2 - Prob. 14ECh. 3.2 - Prob. 15ECh. 3.2 - Prob. 16ECh. 3.2 - Prob. 17ECh. 3.2 - Prob. 18ECh. 3.2 - Prob. 19ECh. 3.2 - Prob. 20ECh. 3.2 - Prob. 21ECh. 3.2 - Prob. 22ECh. 3.2 - Prob. 23ECh. 3.2 - Prob. 24ECh. 3.2 - Prob. 25ECh. 3.2 - Prob. 26ECh. 3.2 - Prob. 27ECh. 3.2 - Prob. 28ECh. 3.2 - Prob. 29ECh. 3.2 - Prob. 30ECh. 3.2 - Prob. 31ECh. 3.2 - Prob. 32ECh. 3.2 - Prob. 33ECh. 3.2 - Prob. 34ECh. 3.2 - Prob. 35ECh. 3.2 - Prob. 36ECh. 3.2 - Prob. 37ECh. 3.2 - Prob. 38ECh. 3.2 - Prob. 39ECh. 3.2 - Prob. 40ECh. 3.2 - Prob. 41ECh. 3.2 - Prob. 42ECh. 3.2 - Prob. 43ECh. 3.2 - Prob. 44ECh. 3.2 - Prob. 45ECh. 3.2 - Prob. 46ECh. 3.2 - Prob. 47ECh. 3.2 - Prob. 48ECh. 3.2 - Prob. 49ECh. 3.2 - Prob. 50ECh. 3.2 - Prob. 51ECh. 3.2 - Prob. 52ECh. 3.2 - Prob. 53ECh. 3.2 - Prob. 54ECh. 3.2 - Prob. 55ECh. 3.2 - Prob. 56ECh. 3.2 - Prob. 57ECh. 3.2 - Prob. 58ECh. 3.2 - Prob. 59ECh. 3.2 - Prob. 60ECh. 3.2 - Prob. 61ECh. 3.3 - Prob. 1ECh. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - Prob. 6ECh. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - Prob. 9ECh. 3.3 - Prob. 10ECh. 3.3 - Prob. 11ECh. 3.3 - Prob. 12ECh. 3.3 - Prob. 13ECh. 3.3 - Prob. 14ECh. 3.3 - Prob. 15ECh. 3.3 - Prob. 16ECh. 3.3 - Prob. 17ECh. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Prob. 20ECh. 3.3 - Prob. 21ECh. 3.3 - Prob. 22ECh. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - Prob. 25ECh. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Prob. 29ECh. 3.3 - Prob. 30ECh. 3.3 - Prob. 31ECh. 3.3 - Prob. 32ECh. 3.3 - Prob. 33ECh. 3.3 - Prob. 34ECh. 3.3 - Prob. 35ECh. 3.3 - Prob. 36ECh. 3.3 - Prob. 37ECh. 3.3 - Prob. 38ECh. 3.3 - Prob. 39ECh. 3.3 - Prob. 40ECh. 3.3 - Prob. 41ECh. 3.3 - Prob. 42ECh. 3.3 - Prob. 1QCh. 3.3 - Prob. 2QCh. 3.3 - Prob. 3QCh. 3.3 - Prob. 4QCh. 3.3 - Prob. 5QCh. 3.3 - Prob. 6QCh. 3.3 - Prob. 7QCh. 3.3 - Prob. 8QCh. 3.3 - Prob. 9QCh. 3.3 - Prob. 10QCh. 3.3 - Prob. 11QCh. 3.3 - Prob. 12QCh. 3.3 - Prob. 13QCh. 3.3 - Prob. 14QCh. 3.3 - Prob. 15QCh. 3.3 - Prob. 16QCh. 3.4 - Prob. 1ECh. 3.4 - Prob. 2ECh. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - Prob. 13ECh. 3.4 - Prob. 14ECh. 3.4 - Prob. 15ECh. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Prob. 19ECh. 3.4 - Prob. 20ECh. 3.4 - Prob. 21ECh. 3.4 - Prob. 22ECh. 3.4 - Prob. 23ECh. 3.4 - Prob. 24ECh. 3.4 - Prob. 25ECh. 3.4 - Prob. 26ECh. 3.4 - Prob. 27ECh. 3.4 - Prob. 28ECh. 3.4 - Prob. 29ECh. 3.4 - Prob. 30ECh. 3.4 - Prob. 31ECh. 3.4 - Prob. 32ECh. 3.4 - Prob. 33ECh. 3.4 - Prob. 34ECh. 3.4 - Prob. 35ECh. 3.4 - Prob. 36ECh. 3.4 - Prob. 37ECh. 3.4 - Prob. 38ECh. 3.4 - Prob. 39ECh. 3.4 - Prob. 40ECh. 3.4 - Prob. 41ECh. 3.4 - Prob. 42ECh. 3.5 - Prob. 1ECh. 3.5 - Prob. 2ECh. 3.5 - Prob. 3ECh. 3.5 - Prob. 4ECh. 3.5 - Prob. 5ECh. 3.5 - Prob. 6ECh. 3.5 - Prob. 7ECh. 3.5 - Prob. 8ECh. 3.5 - Prob. 9ECh. 3.5 - Prob. 10ECh. 3.5 - Prob. 11ECh. 3.5 - Prob. 12ECh. 3.5 - Prob. 13ECh. 3.5 - Prob. 14ECh. 3.5 - Prob. 15ECh. 3.5 - Prob. 16ECh. 3.5 - Prob. 17ECh. 3.5 - Prob. 18ECh. 3.5 - Prob. 19ECh. 3.5 - Prob. 20ECh. 3.5 - Prob. 21ECh. 3.5 - Prob. 22ECh. 3.5 - Prob. 23ECh. 3.5 - Prob. 24ECh. 3.5 - Prob. 25ECh. 3.5 - Prob. 26ECh. 3.5 - Prob. 27ECh. 3.5 - Prob. 28ECh. 3.5 - Prob. 29ECh. 3.5 - Prob. 30ECh. 3.5 - Prob. 31ECh. 3.5 - Prob. 32ECh. 3.5 - Prob. 33ECh. 3.5 - Prob. 34ECh. 3.5 - Prob. 35ECh. 3.5 - Prob. 36ECh. 3.5 - Prob. 37ECh. 3.5 - Prob. 38ECh. 3.5 - Prob. 39ECh. 3.5 - Prob. 40ECh. 3.5 - Prob. 41ECh. 3.5 - Prob. 42ECh. 3.5 - Prob. 43ECh. 3.5 - Prob. 44ECh. 3.5 - Prob. 45ECh. 3.5 - Prob. 46ECh. 3.5 - Prob. 47ECh. 3.5 - Prob. 48ECh. 3.5 - Prob. 49ECh. 3.5 - Prob. 50ECh. 3.5 - Prob. 51ECh. 3.5 - Prob. 52ECh. 3.5 - Prob. 53ECh. 3.5 - Prob. 54ECh. 3.5 - Prob. 55ECh. 3.5 - Prob. 56ECh. 3.5 - Prob. 57ECh. 3.5 - Prob. 58ECh. 3.5 - Prob. 59ECh. 3.5 - Prob. 60ECh. 3.6 - Prob. 1ECh. 3.6 - Prob. 2ECh. 3.6 - Prob. 3ECh. 3.6 - Prob. 4ECh. 3.6 - Prob. 5ECh. 3.6 - Prob. 6ECh. 3.6 - Prob. 7ECh. 3.6 - Prob. 8ECh. 3.6 - Prob. 9ECh. 3.6 - Prob. 10ECh. 3.6 - Prob. 11ECh. 3.6 - Prob. 12ECh. 3.6 - Prob. 13ECh. 3.6 - Prob. 14ECh. 3.6 - Prob. 15ECh. 3.6 - Prob. 16ECh. 3.6 - Prob. 17ECh. 3.6 - Prob. 18ECh. 3.6 - Prob. 19ECh. 3.6 - Prob. 20ECh. 3.6 - Prob. 21ECh. 3.6 - Prob. 22ECh. 3.6 - Prob. 23ECh. 3.6 - Prob. 24ECh. 3.6 - Prob. 25ECh. 3.6 - Prob. 26ECh. 3.6 - Prob. 27ECh. 3.6 - Prob. 28ECh. 3.6 - Prob. 29ECh. 3.6 - Prob. 30ECh. 3.6 - Prob. 31ECh. 3.6 - Prob. 32ECh. 3.6 - Prob. 33ECh. 3.6 - Prob. 34ECh. 3.6 - Prob. 35ECh. 3.6 - Prob. 36ECh. 3.6 - Prob. 37ECh. 3.6 - Prob. 38ECh. 3.6 - Prob. 39ECh. 3.6 - Prob. 40ECh. 3.6 - Prob. 41ECh. 3.6 - Prob. 42ECh. 3.6 - Prob. 43ECh. 3.6 - Prob. 44ECh. 3.6 - Prob. 45ECh. 3.6 - Prob. 46ECh. 3.6 - Prob. 47ECh. 3.6 - Prob. 48ECh. 3.6 - Prob. 49ECh. 3.6 - Prob. 50ECh. 3.6 - Prob. 51ECh. 3.6 - Prob. 52ECh. 3.6 - Prob. 53ECh. 3.6 - Prob. 54ECh. 3.6 - Prob. 55ECh. 3.6 - Prob. 56ECh. 3.6 - Prob. 57ECh. 3.6 - Prob. 58ECh. 3.6 - Prob. 59ECh. 3.6 - Prob. 60ECh. 3.6 - Prob. 61ECh. 3.6 - Prob. 62ECh. 3.6 - Prob. 63ECh. 3.6 - Prob. 64ECh. 3.6 - Prob. 65ECh. 3.6 - Prob. 66ECh. 3.6 - Prob. 67ECh. 3.6 - Prob. 68ECh. 3.6 - Prob. 69ECh. 3.6 - Prob. 70ECh. 3.6 - Prob. 71ECh. 3.6 - Prob. 72ECh. 3.6 - Prob. 73ECh. 3.6 - Prob. 74ECh. 3 - Prob. 1CRCh. 3 - Prob. 2CRCh. 3 - Prob. 3CRCh. 3 - Prob. 4CRCh. 3 - Prob. 5CRCh. 3 - Prob. 6CRCh. 3 - Prob. 7CRCh. 3 - Prob. 8CRCh. 3 - Prob. 9CRCh. 3 - Prob. 10CRCh. 3 - Prob. 11CRCh. 3 - Prob. 12CRCh. 3 - Prob. 13CRCh. 3 - Prob. 14CRCh. 3 - Prob. 15CRCh. 3 - Prob. 16CRCh. 3 - Prob. 17CRCh. 3 - Prob. 18CRCh. 3 - Prob. 19CRCh. 3 - Prob. 20CRCh. 3 - Prob. 21CRCh. 3 - Prob. 22CRCh. 3 - Prob. 23CRCh. 3 - Prob. 24CRCh. 3 - Prob. 25CRCh. 3 - Prob. 26CRCh. 3 - Prob. 27CRCh. 3 - Prob. 28CRCh. 3 - Prob. 1CTCh. 3 - Prob. 2CTCh. 3 - Prob. 3CTCh. 3 - Prob. 4CTCh. 3 - Prob. 5CTCh. 3 - Prob. 6CTCh. 3 - Prob. 7CTCh. 3 - Prob. 8CTCh. 3 - Prob. 9CTCh. 3 - Prob. 10CTCh. 3 - Prob. 11CTCh. 3 - Prob. 12CTCh. 3 - Prob. 13CTCh. 3 - Prob. 14CTCh. 3 - Prob. 15CTCh. 3 - Prob. 16CTCh. 3 - Prob. 1CACh. 3 - Prob. 2CACh. 3 - Prob. 3CACh. 3 - Prob. 4CACh. 3 - Prob. 5CACh. 3 - Prob. 6CACh. 3 - Prob. 7CACh. 3 - Prob. 8CACh. 3 - Prob. 9CACh. 3 - Prob. 10CA
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Numerical anarrow_forward1. Prove the following arguments using the rules of inference. Do not make use of conditional proof. (а) а → (ЪЛс) ¬C ..¬a (b) (pVq) → →r יור (c) (c^h) → j ¬j h (d) s→ d t d -d ..8A-t (e) (pVg) (rv¬s) Лѕ קר .'arrow_forwardThe graph of f(x) is given below. Select each true statement about the continuity of f(x) at x = 1. Select all that apply: ☐ f(x) is not continuous at x = 1 because it is not defined at x = 1. ☐ f(x) is not continuous at x = 1 because lim f(x) does not exist. x+1 ☐ f(x) is not continuous at x = 1 because lim f(x) ‡ f(1). x+→1 ☐ f(x) is continuous at x = 1.arrow_forward
- 2. Consider the following argument: (a) Seabiscuit is a thoroughbred. Seabiscuit is very fast. Every very fast racehorse can win the race. .. Therefore, some thoroughbred racehorse can win the race. Let us define the following predicates, whose domain is racehorses: T(x) x is a thoroughbred F(x) x is very fast R(x) x can win the race : Write the above argument in logical symbols using these predicates. (b) Prove the argument using the rules of inference. Do not make use of conditional proof. (c) Rewrite the proof using full sentences, avoiding logical symbols. It does not need to mention the names of rules of inference, but a fellow CSE 16 student should be able to understand the logical reasoning.arrow_forwardFind the inverse of the matrix, or determine that the inverse does not exist for: € (b) 7 -12 240 1 1 1 (c) 2 3 2 2 17 036 205 20 (d) -1 1 2 1 T NO 1 0 -1 00 1 0 02 (e) 1 0 00 0 0 1 1arrow_forward4. Prove the following. Use full sentences. Equations in the middle of sentences are fine, but do not use logical symbols. (a) (b) (n+3)2 is odd for every even integer n. It is not the case that whenever n is an integer such that 9 | n² then 9 | n.arrow_forward
- 3. (a) (b) Prove the following logical argument using the rules of inference. Do not make use of conditional proof. Vx(J(x)O(x)) 3x(J(x) A¬S(x)) . ·.³x(O(x) ^ ¬S(x)) Rewrite the proof using full sentences, avoiding logical symbols. It does not need to mention the names of rules of inference, but a fellow CSE 16 student should be able to understand the logical reasoning.arrow_forward3. Pleasearrow_forwardWhat does the margin of error include? When a margin of error is reported for a survey, it includes a. random sampling error and other practical difficulties like undercoverage and non-response b. random sampling error, but not other practical difficulties like undercoverage and nonresponse c. practical difficulties like undercoverage and nonresponse, but not random smapling error d. none of the above is corretarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
Finding The Focus and Directrix of a Parabola - Conic Sections; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=KYgmOTLbuqE;License: Standard YouTube License, CC-BY