Chapter 35, Problem 26P

(i)

To determine

To draw: The ray diagram for the given focal lengthy of the lens and the given object distance.

Answer to Problem 26P

The ray diagram of the given criteria is,

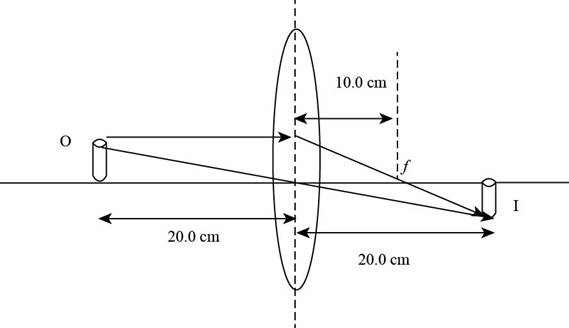
Explanation of Solution

Introduction:

In a ray diagram in the case of lens or mirror the image is formed where two at least refracted or reflected rays coincide with each other.

Given info: The position of object is at $20.0\text{cm}$ and the given focal length is $10.0\text{cm}$.

The ray diagram is shown in the figure below.

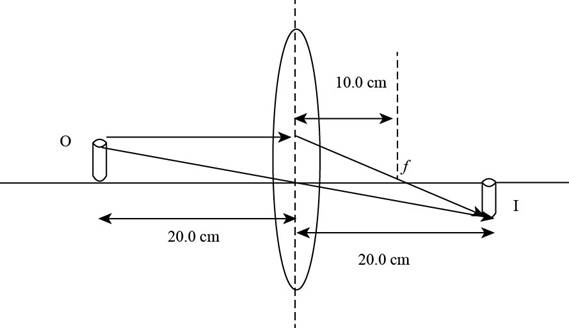
Figure (1)

(ii)

To determine

To draw: The ray diagram for the given focal length of the lens and the given object distance.

Answer to Problem 26P

The ray diagram of the given criteria is,

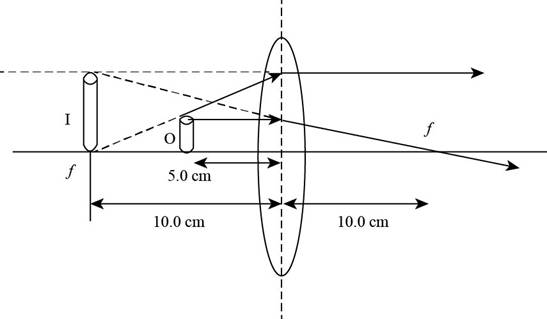
Explanation of Solution

Introduction:

In a ray diagram in the case of lens or mirror the image is formed where two at least refracted or reflected rays coincide with each other.

Given info: The position of object is at $5.00\text{cm}$ and the given focal length is $10.0\text{cm}$.

The ray diagram is shown in the figure below.

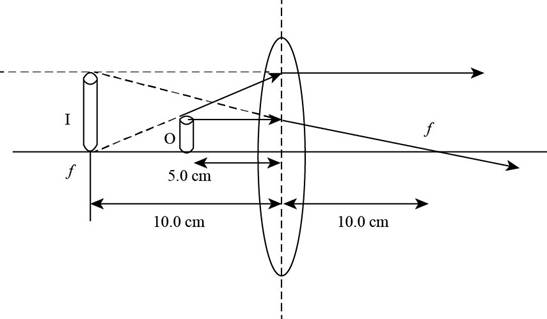
Figure (2)

(a)

To determine

The location of the image the given cases.

Answer to Problem 26P

The image is at $20.0\text{cm}$ behind the lens for the case where object is $20.0\text{cm}$ in front of the lens, and the image is at $10\text{cm}$ in front of the lens when the object is at $5.0\text{cm}$ in front of the lens.

Explanation of Solution

From Figure (1), it is evident that the image is formed on the rear end of the lens and the image distance measured is $20.0\text{cm}$.

From Figure (2), the image is formed at $10.0\text{cm}$ front of the lens at the focal length of the lens.

Conclusion:

Therefore, the measured distance for the image for the case when object is at $20.0\text{cm}$ is $20.0\text{cm}$ back of the mirror and for the case when object is at the $5.00\text{cm}$ is at $10.0\text{cm}$ in front of the lens.

(b)

To determine

The image is real or virtual.

Answer to Problem 26P

For the case when object is at $20.0\text{cm}$ the image is real and for the case object is at $5.00\text{cm}$ the image is virtual.

Explanation of Solution

From Figure (1), it is evident that the image is formed on the rear side and is real and the images formed at the back side of the lens are real.

From Figure (2), the image is formed at $10.00\text{cm}$ front of the lens and the images formed on the front side of the lens are virtual.

Conclusion:

The images formed by the lens in front of it are virtual and erect and images formed on the back side are real and inverted. Hence, image formed by the object kept at. $20\text{cm}$ is real and the image of the object kept at $5.00\text{cm}$ is virtual

(c)

To determine

The image is upright or inverse.

Answer to Problem 26P

For the case when object is at $20.0\text{cm}$ the image is inverted and for the case object is at $5.00\text{cm}$ the image is upright.

Explanation of Solution

From Figure (1), it is evident that the image is formed on the rear side and is real. and

the real images are always inverted

From Figure (2), the image is formed at $10.00\text{cm}$ front of the lens at the images formed on the front side of the lens are virtual.

The virtual images are always upright.

Conclusion:

Therefore, the images formed by the lens in front of it are virtual and erect and images formed on the back side are real and inverted. Hence, image formed by the object kept at. $20.0\text{cm}$ is inverted and the image of the object kept at $5.00\text{cm}$ is upright.

(d)

To determine

The magnification of the image.

Answer to Problem 26P

For the case when object is at $20.0\text{cm}$ the image has magnification $-1.00$ and for the case object is at $5.00\text{cm}$ the magnification is $+2.00$

Explanation of Solution

From Figure (1) it is evident that the image is formed on the rear side and is real and inverted the object height is $1.00\text{cm}$ and the measure height of the image is $1\text{cm}$.

Formula to calculate the magnification is

$M=\frac{-q}{p}$ (1)

$M$ is the magnification.

$q$ is the position of the image.

$p$ is the position of the object.

For the object at $20.0\text{cm}$ substitute $20.0\text{cm}$ for $p$ and $20.0\text{cm}$ for $q$ as the image is inverted.

$\begin{array}{l}M=-\frac{q}{p}\\ =\frac{-20.0\text{cm}}{20.0\text{cm}}\\ =-1.00\end{array}$ (2)

For the object at the distance of $5.00\text{cm}$, substitute $5.0\text{cm}$ for $p$ and $-10.0\text{cm}$ for $q$ as the image is upright in equation (1).

$\begin{array}{l}M=-\frac{q}{p}\\ =-\frac{-10.0\text{cm}}{5.00\text{cm}}\\ =+2.00\end{array}$ (3)

Conclusion:

Therefore, for the case of object at $20\text{cm}$ the magnification is $-1.00$ and for the case  when the object is at the distance of $5.00\text{cm}$ the magnification is $+2.00$.

(e)

To determine

The difference between the value of the ray diagram and the algebraic calculation.

Answer to Problem 26P

The value obtained from the ray diagrams for the cases are same for the values obtained in the algebraic calculation.

Explanation of Solution

Given Info: The focal length of the give lens is $10.0\text{cm}$

From Figure (1) the image distance for the object at $20.0\text{cm}$ the image distance was $+20.0\text{cm}$ at the back of the lens.

For algebraic calculation, the formula for the image distance is,

$\frac{1}{f}=\frac{1}{p}+\frac{1}{q}$ (4)

Here,

$f$ is the focal length of the lens.

$p$ is the object position.

$q$ is the image position.

Substitute $10.0\text{cm}$ for $f$, $20.0\text{cm}$ for $p$ in equation (4),

$\begin{array}{c}\frac{1}{f}=\frac{1}{p}+\frac{1}{q}\\ \frac{1}{10.0\text{cm}}=\frac{1}{20\text{cm}}+\frac{1}{q}\\ \frac{1}{q}=\frac{1}{20\text{cm}}\\ q=+20.0\text{cm}\end{array}$ (5)

Form figure (1) the magnification is $-1.00$ as the height of image is equal to height of object.

Formula to calculate the magnification of the image

$M=-\frac{q}{p}$ (6)

Here

$M$ is the magnification.

Substitute $20.0\text{cm}$ for $p$ and $+20.0\text{cm}$ for $q$ from equation (5) in equation (6)

$\begin{array}{c}M=-\frac{q}{p}\\ =-\frac{+20.0\text{cm}}{20.0\text{cm}}\\ =-1.00\end{array}$ (7)

From figure (2) the image distance is $10.0\text{cm}$ in front of the mirror for the given object distance $5.00\text{cm}$.

From equation (4) formula to calculate the image distance is,

$\frac{1}{f}=\frac{1}{p}+\frac{1}{q}$

Substitute $10.0\text{cm}$ for $f$ and $5.00\text{cm}$ for $p$ in above equation,

$\begin{array}{c}\frac{1}{f}=\frac{1}{p}+\frac{1}{q}\\ \frac{1}{10.0\text{cm}}=\frac{1}{5.00\text{cm}}+\frac{1}{q}\\ q=-10.0\text{cm}\end{array}$ (8)

The image distance is $10.0\text{cm}$ in front of the mirror.

From equation (6) the formula to calculate the magnification is,

$M=-\frac{q}{p}$

Substitute $-10.0\text{cm}$ for $q$ and $5.00\text{cm}$ for $p$ in the above equation.

$\begin{array}{l}M=-\frac{q}{p}\\ M=-\left(\frac{-10.0\text{cm}}{5.00\text{cm}}\right)\\ M=+2.00\end{array}$ (9)

From equation (6) and equation (7) it is evident that for the case of object at $20\text{cm}$ the image distance and the magnification is same as in the case for the ray diagram, the image distance is positive hence the image is behind the lens thus, the image is real and magnification is negative hence the image is inverted.

From equation (8) and (9) the image distance and magnification is same for the ray diagram and the algebraic case when the object is $5.00\text{cm}$. The image distance is negative hence a virtual image is formed and the magnification is in positive therefore the image is upright.

Conclusion:

Therefore, the result for the ray diagrams and algebraic calculations are same.

(f)

To determine

The difficulties is making the graph which may lead to difference between the algebraic and graphical values.

Answer to Problem 26P

Human hand errors, Parallax errors and scale measurement errors could lead to difference in the values of graph and algebraic calculation.

Explanation of Solution

While drawing the graph the possible errors are human hand errors, parallax errors and scale measurement errors.

Human Hand Errors are while making the ray diagrams the rays might not converge with extreme precision. Parallax error/Human eye errors occur due to human eye. Scale errors are during the scale measurement.

Conclusion:

Therefore, the three most common errors that can lead to difficulties in constructing the graph which might lead to change the algebraic and graphical values are human hand errors, parallax errors and Scale errors.