
(a).
The sketch of the graph of electric field for the given wave at time
(a).
Answer to Problem 70AP
The sketch of the graph of electric field for the given wave at time
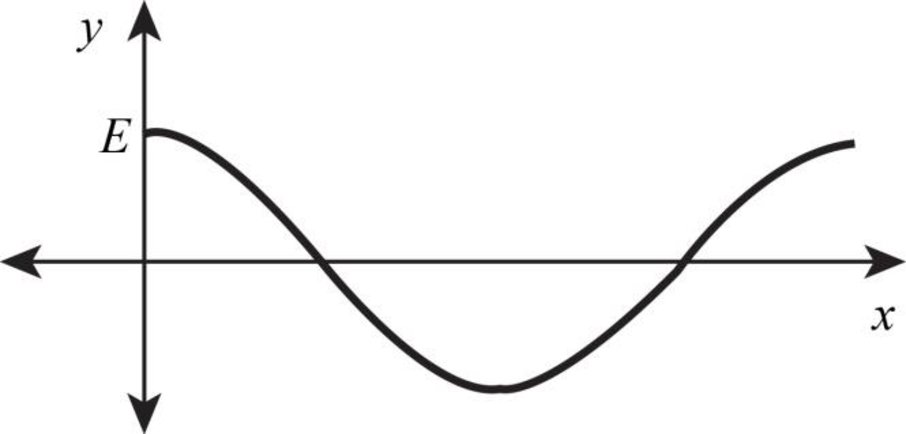
Explanation of Solution
The sketch the graph of electric field for the given wave at time
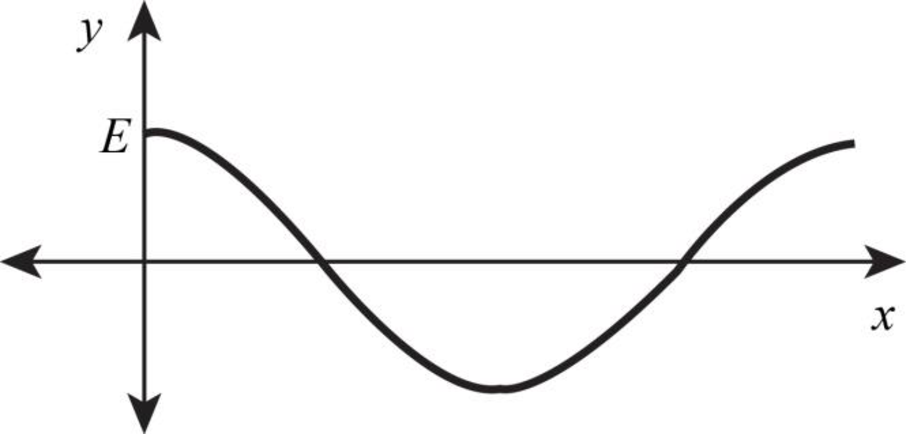
Figure-(1)
(b).
The energy density in the electric field as a function of
(b).
Answer to Problem 70AP
The energy density in the electric field as a function of
Explanation of Solution
Write the equation for the electric field varying in
Here,
Write the expression for the energy density in terms of electric field.
Here,
Substitute
Conclusion:
Substitute
Therefore, the energy density in the electric field as a function of
(c).
The energy density in the magnetic field as a function of
(c).
Answer to Problem 70AP
The energy density in the magnetic field as a function of
Explanation of Solution
Write the equation for the magnetic field varying in
Here,
Write the expression for the energy density in terms of magnetic field.
Here,
Substitute
Conclusion:
Substitute
Therefore, the energy density in the magnetic field as a function of
(d).
The total energy density as a function of
(d).
Answer to Problem 70AP
The total energy density as a function of
Explanation of Solution
Write the expression for the total energy density.
Substitute
Write the relation between the electric and the magnetic field.
Substitute
Substitute
Therefore, the total energy density as a function of
(e).
The energy in the "shoebox" in terms of
(e).
Answer to Problem 70AP
The energy in the "shoebox" in terms of
Explanation of Solution
Write the given equation for energy.
Here,
Substitute
Write the expression for the wave vector.
Substitute
`
Therefore, the energy in the "shoebox" in terms of
(f).
The power the wave carries through the area
(f).
Answer to Problem 70AP
The power the wave carries through the area
Explanation of Solution
Write the expression for power through an area
Here,
Substitute
Also,
Here,
Substitute
Therefore, the power the wave carries through the area
(g).
The intensity in terms of
(g).
Answer to Problem 70AP
The intensity in terms of
Explanation of Solution
Write the expression for intensity.
Here,
Substitute
Also,
Substitute
Therefore, the intensity in terms of
(h).
The comparison of the result in part
(h).
Answer to Problem 70AP
On comparison of equation (XVIII) and (XIX), both the equation yields the same result for the intensity. Therefore, the intensity is same for both the conditions.
Explanation of Solution
The equation (34.24) is,
The result obtained in part
On comparison of equation (XVIII) and (XIX), both the equation yields the same result for the intensity. Therefore, the intensity is same for both the conditions.
Want to see more full solutions like this?
Chapter 34 Solutions
Physics for Scientists and Engineers With Modern Physics
- A person on horseback is on a drawbridge which is at an angle = 20.0° above the horizontal, as shown in the figure. The center of mass of the person-horse system is d = 1.35 m from the end of the bridge. The bridge is l = 7.00 m long and has a mass of 2,300 kg. A cable is attached to the bridge 5.00 m from the frictionless hinge and to a point on the wall h = 12.0 m above the bridge. The mass of person plus horse is 1,100 kg. Assume the bridge is uniform. Suddenly (and most unfortunately for the horse and rider), the ledge where the bridge usually rests breaks off, and at the same moment the cable snaps and the bridge swings down until it hits the wall. ÚI MAJI A TLA MAJA AUTA (a) Find the angular acceleration (magnitude, in rad/s²) of the bridge once it starts to move. 2.22 Use the rotational analogue of Newton's second law. The drawbridge can be modeled as a rod, with rotation axis about one end. rad/s² (b) How long (in s) does the horse and rider stay in contact with the bridge…arrow_forwardTwo long, parallel wires carry currents of I₁ = 2.70 A and I2 = 4.85 A in the directions indicated in the figure below, where d = 22.0 cm. (Take the positive x direction to be to the right.) 12 (a) Find the magnitude and direction of the magnetic field at a point midway between the wires. magnitude direction 3.91 270 μπ ⚫ counterclockwise from the +x axis (b) Find the magnitude and direction of the magnetic field at point P, located d = 22.0 cm above the wire carrying the 4.85-A current. magnitude direction Your response differs significantly from the correct answer. Rework your solution from the beginning and check each step carefully. μT The response you submitted has the wrong sign.° counterclockwise from the +x axisarrow_forwardO Macmillan Learning The mass of a particular eagle is twice that of a hunted pigeon. Suppose the pigeon is flying north at Vi2 = 16.1 m/s when the eagle swoops down, grabs the pigeon, and flies off. At the instant right before the attack, the eagle is flying toward the pigeon at an angle 0 = 64.3° below the horizontal and a speed of Vi,1 = 37.9 m/s. What is the speed of of the eagle immediately after it catches its prey? What is the magnitude & of the angle, measured from horizontal, at which the eagle is flying immediately after the strike? Uf = II x10 TOOLS Vi.1 Vi,2 m/sarrow_forward
- What is the equivalent resistance if you connect a 1.7 Ohm, a 9.3 Ohm, and a 22 Ohm resistor in series? (Give your answer as the number of Ohms.)arrow_forwardThree wires meet at a junction. One wire carries a current of 5.2 Amps into the junction, and a second wire carries a current of 3.7 Amps out of the junction. What is the current in the third wire? Give your answer as the number of Amps, and give a positive number if the current in that wire flows out of the junction, or a negative number if the current in that wire flows into the junction.arrow_forwardWhat is the equivalent resistance if you connect a 4.5 Ohm, a 6.8 Ohm, and a 15 Ohm resistor in parallel? (Give your answer as the number of Ohms.)arrow_forward
- Suppose a heart defibrillator passes 10.5 Amps of current through a patient's torso for 5.0 x 10-3 seconds in order to restore a regular heartbeat. The voltage across the defibrillator is 9800 volts for the entire time that current is flowing. If 7.25 kg of body tissue is involved, with a specific heat of 3500 J/(kg°C), then what is the resulting temperature increase of the person's torso? (Give your answer as the number of degrees C.)arrow_forwardThe figure below is a cross-sectional view of a coaxial cable. The center conductor is surrounded by a rubber layer, an outer conductor, and another rubber layer. In a particular application, the current in the inner conductor is I₁ = 1.04 A out of the page and the current in the outer conductor is I2 = 2.90 A into the page. Assuming the distance d = 1.00 mm, answer the following. 4 12 (a) Determine the magnitude and direction of the magnetic field at point a. magnitude 208 direction upward (b) Determine the magnitude and direction of the magnetic field at point b. magnitude direction 238 You can approach this problem by finding the field produced by current I₁ and the field produced by I2 and then adding them vectorially. μT downwardarrow_forwardShoto, from My Hero Academia, has a power (or a “quirk”) that allows him to make large amounts of ice from nothing. Let us say that due to a fire a 361 kg steel beam is heated to 943.˚C and Shoto creates 390. kg of ice at 0.00˚C around it to cool it down. What is the final temperature of the system after the ice melts and it reaches thermal equilibrium? The specific heat of steel is 502 J/kg˚C. The specific heat of water is 4186 J/kg˚C. The latent heat of fusion for ice is 3.33⋅10^5 J/kg.arrow_forward
- A 25.0 cm long organ pipe is filled with air and is open at one end and closed at the other. The speed of sound in air at 0°C is 331 m/s. What is the frequency of the fourth mode of vibration? Multiple Choice О 1,550 Hz О 1,750 Hz О 2,320 Hz О 2,720 Hz О 3,170 Hzarrow_forward23.4 g of coffee beans at room temperature (18.6 °C) is mixed into 316 g of water at 96.8 °C in an effort to make coffee. The entire system is poured in a 363 g ceramic mug. Assume the mug is initally also at room temperature (18.6 °C). What is the final temperature of the mixture? The specific heat of ground coffee beans is 1670 J/kg˚C, the specific heat of water is 4186 J/kg˚C, and the specific heat of the mug is 850. J/kg˚C.arrow_forwardSnoop Dogg, in an effort to get laid back (with his mind on his money and his money on his mind) pours himself a gin and juice. He mixes 0.124 kg (about 3 shots) of gin with 0.576 kg (about a pint) of orange juice. The gin starts at 20.0˚C, room temperature. The juice is refrigerated and starts at 2.89 ˚C. What is the final temperature after mixing of the gin and juice? The specific heat of gin is 3460 J/kg˚C and the specific heat of orange juice is 3730 J/kg˚C.arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





