Chapter 3.3, Problem 95E

a.

To determine

Plot the data points $(t,T)$ and $(t,T-21)$ .

Answer to Problem 95E

  

  

Explanation of Solution

Given information:

A cup of water at an initial temperature of ${78}^{\circ }C$ is placed in a room at a constant temperature of ${21}^{\circ }C$ . The temperature of the water is measured every $5$ minutes during a half−hour period. The results are recorded as ordered pairs of the form $(t,T)$ , where is the time (in minutes) and is the temperature (in degree celsius).

  $(0,{78.0}^{\circ }),(5,{66.0}^{\circ }),(10,{57.5}^{\circ }),(15,{51.2}^{\circ }),(20,{46.3}^{\circ }),(25,{42.4}^{\circ }),(30,{39.6}^{\circ })$

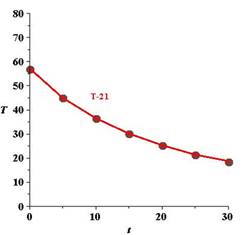
The graph of the model for the data should be asymptotic with the graph of the temperature of the room. Subtract the room temperature from each of the temperatures in the ordered pairs. Usa a graphing utility to plot the data points $(t,T)$ and $(t,T-21)$ .

Calculation:

The initial temperature of ${78}^{\circ }C$ is placed in a room at a constant temperature of ${21}^{\circ }C$ . The temperature of the water is measured every $5$ minutes and the results are shown in the table below:

  $\begin{array}{cc}t(\text{in min})& 0 \text{5} \text{1}0 \text{15} \text{2}0 \text{25} \text{3}0\\ T-21(\text{in C})& \text{78} \text{66} \text{57}.\text{7} \text{51}.\text{2} \text{46}.\text{3} \text{42}.\text{4} \text{39}.\text{6}\end{array}$

After subtracting the room temperature, the result is shown in the table below:

  $\begin{array}{cc}t(\text{in min})& 0 \text{5} \text{1}0 \text{15} \text{2}0 \text{25} \text{3}0\\ T-21(\text{in C})& 57 45 36.5 30.2 25.3 21.4 18.6\end{array}$

The graph corresponding to $(t,T)$ and $(t,T-21)$ is given below:

  

  

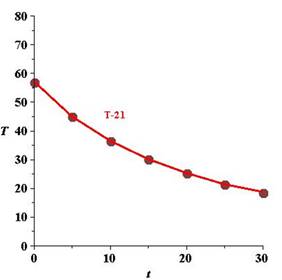
Hence, the result.

b.

To determine

Solve for $T$ and graph the model.

Compare the result.

Answer to Problem 95E

  

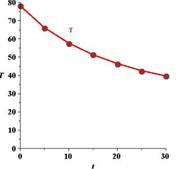
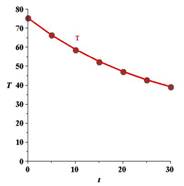
There is not much variation between the two graphs.

Explanation of Solution

Given information:

A cup of water at an initial temperature of ${78}^{\circ }C$ is placed in a room at a constant temperature of ${21}^{\circ }C$ . The temperature of the water is measured every $5$ minutes during a halfg −hour period. The results are recorded as ordered pairs of the form $(t,T)$ , where is the time (in minutes) and is the temperature (in degree celsius).

  $(0,{78.0}^{\circ }),(5,{66.0}^{\circ }),(10,{57.5}^{\circ }),(15,{51.2}^{\circ }),(20,{46.3}^{\circ }),(25,{42.4}^{\circ }),(30,{39.6}^{\circ })$ .

An exponential model for the data $(t,T-21)$ is given by $T-21=54.4{(0.964)}^t$ . Solve for $T$ and graph the model. Compare the result with the plot of the original data.

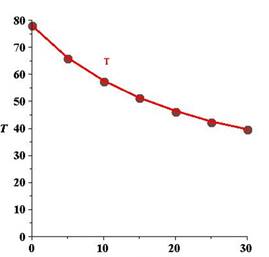
Calculation:

The initial temperature of ${78}^{\circ }C$ is placed in a room at a constant temperature of ${21}^{\circ }C$ . The temperature of the water is measured every $5$ minutes and the results are shown in the table below:

  $\begin{array}{cc}t(\text{in min})& 0 \text{5} \text{1}0 \text{15} \text{2}0 \text{25} \text{3}0\\ T-21(\text{in C})& \text{78} \text{66} \text{57}.\text{7} \text{51}.\text{2} \text{46}.\text{3} \text{42}.\text{4} \text{39}.\text{6}\end{array}$

The exponential model for the data $(t,T-21)$ is given by $T-21=54.4{(0.964)}^t$ .

By giving different values to $t$ , $T$ is determined and given in the table below:

  $\begin{array}{cc}t(\text{in min})& 0 \text{5} \text{1}0 \text{15} \text{2}0 \text{25} \text{3}0\\ T-21(\text{in C})& \text{75}\text{.4} \text{66}\text{.3} \text{58}.\text{7} \text{52}.4 \text{47}.1 \text{42}.8 \text{39}.1\end{array}$

The graph corresponding to the model is given below:

  

  

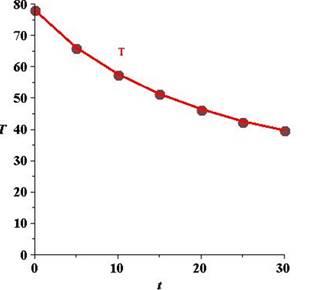
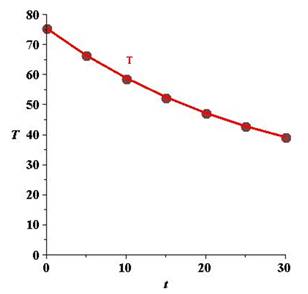
Hence, on compairing the model output with the original data we will see that there is not much variation between the two graphs..

c.

To determine

Solve for $T$ , and verify that the result is equivalent to the model in part b.

Answer to Problem 95E

  ${\boxed{T-21=54.4\left(0.964\right)}}^t$.

This equation is equivalent to model equation.

Explanation of Solution

Given information:

A cup of water at an initial temperature of ${78}^{\circ }C$ is placed in a room at a constant temperature of ${21}^{\circ }C$ . The temperature of the water is measured every $5$ minutes during a halfg −hour period. The results are recorded as ordered pairs of the form $(t,T)$ , where is the time (in minutes) and is the temperature (in degree celsius).

  $(0,{78.0}^{\circ }),(5,{66.0}^{\circ }),(10,{57.5}^{\circ }),(15,{51.2}^{\circ }),(20,{46.3}^{\circ }),(25,{42.4}^{\circ }),(30,{39.6}^{\circ })$

Take the natural logrithms of the revised temperatures. Use the graphing utility to plot the points $(t,\ln (T-21))$ and observe that the points appear to be linear. Use the regression feature of the graphing utility to fit a line to these data. This resulting line has the form $\ln (T-21)=at+b$ . Solve for $T$ , and verify that the result is equivalent to the model in part b.

Calculation:

The initial temperature of ${78}^{\circ }C$ is placed in a room at a constant temperature of ${21}^{\circ }C$ . The temperature of the water is measured every $5$ minutes and the results are shown in the table below:

  $\begin{array}{cc}t(\text{in min})& 0 \text{5} \text{1}0 \text{15} \text{2}0 \text{25} \text{3}0\\ T-21(\text{in C})& \text{78} \text{66} \text{57}.\text{7} \text{51}.\text{2} \text{46}.\text{3} \text{42}.\text{4} \text{39}.\text{6}\end{array}$

After subtracting the room temperature, the result is shown in the table below:

  $\begin{array}{cc}t(\text{in min})& 0 \text{5} \text{1}0 \text{15} \text{2}0 \text{25} \text{3}0\\ T-21(\text{in C})& 57 45 36.5 30.2 25.3 21.4 18.6\end{array}$

Taking the natural logarithm of the revised temperature, $\ln (T-21)$ is listed in the table below:

  $\begin{array}{cc}t(\text{in min})& 0 \text{5} \text{1}0 \text{15} \text{2}0 \text{25} \text{3}0\\ T-21(\text{in C})& 4.043 3.807 3.597 3.408 3.231 3.063 2.923\end{array}$

The graph corresponding to $(t,\ln (T-21))$ is given below:

  

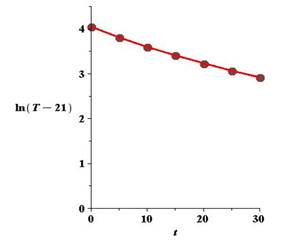
The slope of the line is calculated by taking any two points. So let us consider these points as $(5,3.807)$ and $(25,3.063)$ so,

  $m=\begin{array}{c}3.063-3.087\\ 25-5\end{array}$

  $=-0.037$

By the point-slope form, the equation of the line is,

  $\begin{array}{l}Y-Y_1=m(X-X_1)\\ Y-3.087=-0.037(X-5)\end{array}$

where $Y$

  $=\ln (T-21)$ , $X$

  $=$

  $t$ .

  $\begin{array}{l}\ln (T-21)-3.087=-0.037t+0.185\\ \ln (T-21)=-0.037t+3.992\end{array}$

Now, solving for $T$ , we get,

  $\begin{array}{l}T-21=e^{-0.037+3.992}\\ T-21=e^{-0.337}{e}^{3.992}\\ \boxed{T-21=54.4{\left(0.964\right)}^t}\end{array}$

Hence, the above equation is equivalent to model equation.

d.

To determine

Solve for $T$ ,and use the graphing utility to graph the rational function and the original data points.

Answer to Problem 95E

  $\boxed{T=21+\begin{array}{c}1\\ \left(0.001t+0.017\right)\end{array}}$

  

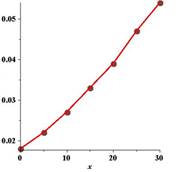
Explanation of Solution

Given information:

A cup of water at an initial temperature of ${78}^{\circ }C$ is placed in a room at a constant temperature of ${21}^{\circ }C$ . The temperature of the water is measured every $5$ minutes during a halfg −hour period. The results are recorded as ordered pairs of the form $(t,T)$ , where is the time (in minutes) and is the temperature (in degree celsius).

  $(0,{78.0}^{\circ }),(5,{66.0}^{\circ }),(10,{57.5}^{\circ }),(15,{51.2}^{\circ }),(20,{46.3}^{\circ }),(25,{42.4}^{\circ }),(30,{39.6}^{\circ })$ .

Fit a rational model to the data. Take the recprocals of the $y$ -coordinates of the revised data points to $(t,\begin{array}{c}1\\ T-21\end{array})$ .

Use the graphing utility to graph these points and observe that the points appear to be linear. Use the regression feature of the graphing utility to fit a line to these data. This resulting line has the form $\begin{array}{c}1\\ T-21\end{array}=at+b$ .

Solve for $T$ ,and use the graphing utility to graph the rational function and the original data points.

Calculation:

The initial temperature of ${78}^{\circ }C$ is placed in a room at a constant temperature of ${21}^{\circ }C$ . The temperature of the water is measured every $5$ minutes and the results are shown in the table below:

  $\begin{array}{cc}t(\text{in min})& 0 \text{5} \text{1}0 \text{15} \text{2}0 \text{25} \text{3}0\\ T-21(\text{in C})& \text{78} \text{66} \text{57}.\text{7} \text{51}.\text{2} \text{46}.\text{3} \text{42}.\text{4} \text{39}.\text{6}\end{array}$

Now, on taking the reciprocals of the $y$ -coordinateswe generate the point $(t,\begin{array}{c}1\\ T-21\end{array})$ .as given in the table below:

  $\begin{array}{cc}t(\text{in min})& 0 \text{5} \text{1}0 \text{15} \text{2}0 \text{25} \text{3}0\\ T-21(\text{in C})& 0.018 0.022 0.027 0.033 0.039 0.047 0.054\end{array}$

The graph corresponding to $(t,\begin{array}{c}1\\ T-21\end{array})$ is given below:

  

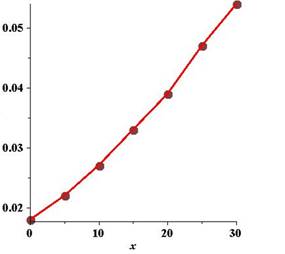
The slope of the line is calculated by taking any two points. So let us consider these points as $5,0.022)$ and $(20,0.039)$ so,

  $m=\begin{array}{c}0.039-30.022\\ 20-5\end{array}$

  $=0.001$

By the point-slope form, the equation of the line is,

  $\begin{array}{l}Y-Y_1=m(X-X_1)\\ Y-0.022=-0.001(X-5)\end{array}$

where $Y$

  $=$

  $\begin{array}{c}1\\ T-21\end{array}$ , $X$

  $=$

  $t$ .

  $\begin{array}{l}\begin{array}{c}1\\ T-21\end{array}-0.022=0.001t-0.005\\ \begin{array}{c}1\\ T-21\end{array}=0.001t+0.017\end{array}$

The above equation has the form $\begin{array}{c}1\\ T-21\end{array}=at+b$ .

Now, solving for $T$ , we get,

  $\begin{array}{l}\begin{array}{c}1\\ \left(0.001t+0.017\right)\end{array}=T-21\\ T=21+\begin{array}{c}1\\ \left(0.001t+0.017\right)\end{array}\end{array}$

Hence, $\boxed{T=21+\begin{array}{c}1\\ \left(0.001t+0.017\right)\end{array}}$ .

e.

To determine

Why did taking the logarithms and reciprocals of the temperatures lead to a linear scatter plot?

Answer to Problem 95E

Both the logarithmic and reciprocal functions of time vary linearly.

Explanation of Solution

Given information:

A cup of water at an initial temperature of ${78}^{\circ }C$ is placed in a room at a constant temperature of ${21}^{\circ }C$ . The temperature of the water is measured every $5$ minutes during a halfg −hour period. The results are recorded as ordered pairs of the form $(t,T)$ , where is the time (in minutes) and is the temperature (in degree celsius).

  $(0,{78.0}^{\circ }),(5,{66.0}^{\circ }),(10,{57.5}^{\circ }),(15,{51.2}^{\circ }),(20,{46.3}^{\circ }),(25,{42.4}^{\circ }),(30,{39.6}^{\circ })$

Why did taking the logarithms of the temperatures lead to a linear scatter plot? Why did taling the reciprocals of the temperatures lead to a linear sactter plot?

Calculation:

Both the logarithmic and reciprocal functions of time vary linearly.

Hence, the scatter plot gives a linear plot.