Chapter 3.3, Problem 53E

Solution

To graph: The given function and to analyze it.

  

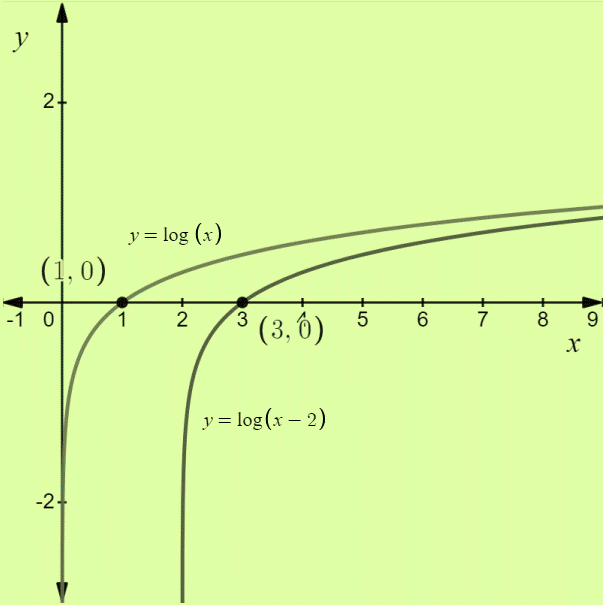
The domain is $\left(2,\infty \right)$ .

The range is $\left(-\infty ,\infty \right)$ .

It is a continuous function.

Always increasing.

Not bounded.

No local extrema.

No symmetry.

No horizontal asymptotes.

The vertical asymptote is $x=2$ .

End behavior: $\underset{x\to \infty }{\lim }f\left(x\right)=\infty$

Given:

  $f\left(x\right)=\log \left(x-2\right)$

Concept used:

The graph of $f\left(x-k\right)$ is obtained by shifting the graph of $f\left(x\right)$ to the right side by $k$ units.

Calculation:

Start with the graph of $y=\log x$ , then shift 2 units right.

So, the graph of the given function is

  

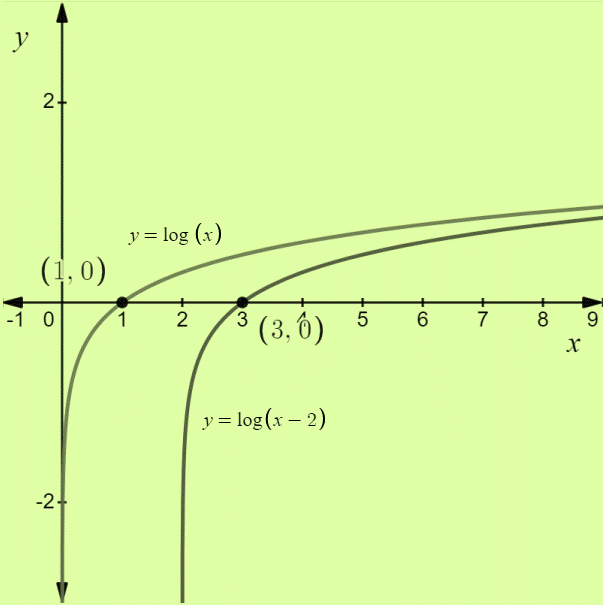
The given function is well defined for all real numbers greater than 2, therefore the domain is $\left(2,\infty \right)$ .

The range is $\left(-\infty ,\infty \right)$ .

From the graph, it can be seen that the curve has no breaks or jumps; therefore it is a continuous function.

From the graph, it can be seen that the value of $y$ increases as the value of $x$ increases from $2$ to $\infty$ .

Therefore, the function is always increasing.

The function is not bounded.

There are no turning points for the given curve, so there is no local extrema.

The curve is neither symmetric with the $x$ -axis nor with the $y$ -axis.

So the curve has no symmetry.

There are no horizontal asymptotes.

The vertical asymptote is $x=2$ .

End behavior:

From the graph, it can be seen that $y\to \infty$ as $x\to \infty$ . So,

  $\underset{x\to \infty }{\lim }f\left(x\right)=\infty$