
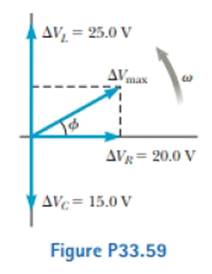
Review. The voltage phasor diagram for a certain series RLC circuit is shown in Figure P33.59. The resistance of the circuit is 75.0 Ω, and the frequency is 60.0 Hz. Find (a) the maximum voltage ΔVmax, (b) the phase angle ϕ, (c) the maximum current, (d) the impedance, (e) the capacitance and (f) the inductance of the circuit, and (g) the average power delivered to the circuit.
(a)
The maximum voltage.
Answer to Problem 33.59AP
The maximum voltage is
Explanation of Solution
Given info: The resistance of the circuit is
The expression for maximum value of the voltage is,
Here,
Substitute
Conclusion:
Therefore, the maximum voltage is
(b)
The phase angle.
Answer to Problem 33.59AP
The phase angle is
Explanation of Solution
Given info: The resistance of the circuit is
The expression for the phase angle is,
Substitute
Conclusion:
Therefore, the phase angle is
(c)
The maximum current.
Answer to Problem 33.59AP
The maximum current is
Explanation of Solution
Given info: The resistance of the circuit is
The expression for maximum current is,
Here,
Substitute
Conclusion:
Therefore, the maximum current is
(d)
The impedance.
Answer to Problem 33.59AP
The impedance is
Explanation of Solution
Given info: The resistance of the circuit is
The expression for the impedance is,
Substitute
Conclusion:
Therefore, the impedance is
(e)
The capacitance.
Answer to Problem 33.59AP
The capacitance is
Explanation of Solution
Given info: The resistance of the circuit is
The circuit is series
The expression capacitive reactance is,
Substitute
The expression capacitive reactance in terms of the capacitance is,
Here,
Rearrange the above equation for the value of capacitance.
Substitute
Conclusion:
Therefore, the capacitance is
(f)
The inductance of the circuit.
Answer to Problem 33.59AP
The inductance of the circuit
Explanation of Solution
Given info: The resistance of the circuit is
The circuit is series
The expression inductive reactance is,
Substitute
Thus the value of inductive reactance is
The expression inductive reactance in terms of the inductance is,
Here,
Rearrange the above equation for the value of inductance.
Substitute
Conclusion:
Therefore, the inductance is
(g)
The average power delivered to circuit.
Answer to Problem 33.59AP
The average power delivered to circuit is
Explanation of Solution
Given info: The resistance of the circuit is
The expression for R.M.S value of the current is,
The expression for the average power delivered is,
Substitute
Substitute
Conclusion:
Therefore, the average power delivered to circuit is
Want to see more full solutions like this?
Chapter 33 Solutions
Physics for Scientists and Engineers (AP Edition)
- help because i am so lost and it should look something like the picturearrow_forward3.31 A Ferris wheel with radius Figure E3.31 14.0 m is turning about a horizontal axis through its center (Fig. E3.31). The linear speed of a passenger on the rim is constant and equal to 6.00 m/s. What are the magnitude and direction of the passenger's acceleration as she passes through (a) the lowest point in her circular motion and (b) the high- est point in her circular motion? (c) How much time does it take the Ferris wheel to make one revolution?arrow_forward1.56 ⚫. Three horizontal ropes pull on a large stone stuck in the ground, producing the vector forces A, B, and C shown in Fig. P1.56. Find the magnitude and direction of a fourth force on the stone that will make the vector sum of the four forces zero. Figure P1.56 B(80.0 N) 30.0 A (100.0 N) 53.0° C (40.0 N) 30.0°arrow_forward
- 1.39 Given two vectors A = -2.00 +3.00 +4.00 and B=3.00 +1.00 -3.00k. (a) find the magnitude of each vector; (b) use unit vectors to write an expression for the vector difference A - B; and (c) find the magnitude of the vector difference A - B. Is this the same as the magnitude of B - Ä? Explain.arrow_forward5. The radius of a circle is 5.5 cm. (a) What is the circumference in meters? (b) What is its area in square meters? 6. Using the generic triangle below, solve the following: 0 = 55 and c = 32 m, solve for a and b. a = 250 m and b = 180 m, solve for the angle and c. b=104 cm and c = 65 cm, solve for a and the angle b a 7. Consider the figure below representing the Temperature (T in degrees Celsius) as a function of time t (in seconds) 4 12 20 (a) What is the area under the curve in the figure below? (b) The area under the graph can be calculated using integrals or derivatives? (c) During what interval is the derivative of temperature with respect to time equal to zero?arrow_forwardPart 3: Symbolic Algebra Often problems in science and engineering are done with variables only. Don't let the different letters confuse you. Manipulate them algebraically as though they were numbers. 1. Solve 3x-7= x + 3 for x 2x-1 2. Solve- for x 2+2 In questions 3-11 solve for the required symbol/letter 3. v2 +2a(s-80), a = = 4. B= Ho I 2π r 5. K = kz² 6.xm= MAL ,d= d 7.T, 2 = 8.F=Gm 9. mgh=mv² 10.qV = mu² 80 12. Suppose that the height in meters of a thrown ball after t seconds is given by h =6+4t-t². Complete the square to find the highest point and the time when this happens. 13. Solve by completing the square c₁t² + cat + 3 = 0. 14. Solve for the time t in the following expression = 0 + vot+at²arrow_forward
- A blacksmith cools a 1.60 kg chunk of iron, initially at a temperature of 650.0° C, by trickling 30.0°C water over it. All the water boils away, and the iron ends up at a temperature of 120.0° C. For related problem-solving tips and strategies, you may want to view a Video Tutor Solution of Changes in both temperature and phase. Part A How much water did the blacksmith trickle over the iron? Express your answer with the appropriate units. HÅ mwater = Value 0 ? Units Submit Request Answerarrow_forwardSteel train rails are laid in 13.0-m-long segments placed end to end. The rails are laid on a winter day when their temperature is -6.0° C. Part A How much space must be left between adjacent rails if they are just to touch on a summer day when their temperature is 32.0°C? Express your answer with the appropriate units. ☐ о μΑ ? D = Value Units Submit Previous Answers Request Answer × Incorrect; Try Again; 3 attempts remaining Al Study Tools Looking for some guidance? Let's work through a few related practice questions before you go back to the real thing. This won't impact your score, so stop at anytime and ask for clarification whenever you need it. Ready to give it a try? Start Part B If the rails are originally laid in contact, what is the stress in them on a summer day when their temperature is 32.0°C? Express your answer in pascals. Enter positive value if the stress is tensile and negative value if the stress is compressive. F A Ο ΑΣΦ ? Раarrow_forwardhelp me with this and the step I am so confused. It should look something like the figure i shownarrow_forward
- Part A In an effort to stay awake for an all-night study session, a student makes a cup of coffee by first placing a 200 W electric immersion heater in 0.250 kg of water. How much heat must be added to the water to raise its temperature from 20.5° C to 95.0°C? Express your answer in joules. ΕΠΙ ΑΣΦ Q Submit Request Answer Part B ? J How much time is required? Assume that all of the heater's power goes into heating the water. Express your answer in seconds. VG ΑΣΦ ? t = Sarrow_forwardhelp i dont understand this it should look like something like this picture. help me with the stepsarrow_forwardDraw the velocity vectors starting at the black dots and the acceleration vectors including those equal to zero.arrow_forward
 Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
 Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





