Essentials of Statistics Books a la carte Plus NEW MyLab Statistics with Pearson eText - Access Card Package (5th Edition)
5th Edition
ISBN: 9780133892697
Author: Mario F. Triola
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 3.3, Problem 19BSC
In Exercises 5-20, find the
18. Freshman 15 According to the “freshman 15” legend, college freshmen gain 15 pounds (or 6.8 kilograms) during their freshman year. Listed below are the amounts of weight change (in kilograms) for a simple random sample of freshmen included in a study (“Changes in Body Weight and Fat Mass of Men and Women in the First Year of College: A Study of the ‘Freshman 15’” by Hoffman, Policastro, Quick, and Lee, Journal of American College Health, Vol. 55, No. 1). Positive values correspond to students who gained weight and negative values correspond to students who lost weight. Is a weight gain of 15 pounds (or 6.8 kg) unusual? Why or why not? If 15 pounds (or 6.8 kg) is not unusual, does that support the legend of the “freshman 15”?
Expert Solution & Answer
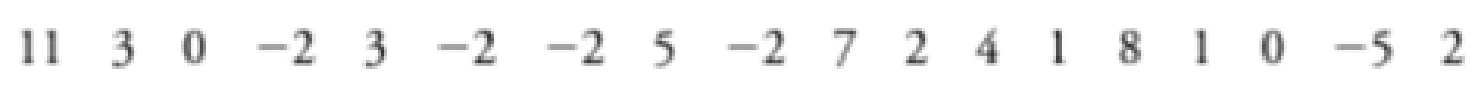
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
17. Suppose that X1, X2,..., Xn are random variables, such that E|xk| < ∞ for
all k, and set Yn = max1
6. Show that, for any random variable, X, and a > 0,
L
P(x < X ≤ x+a) dx = a.
2015
15. This problem extends Problem 20.6. Let X, Y be random variables with finite
mean. Show that
(P(X ≤ x ≤ Y) - P(Y < x ≤ X))dx = E Y — E X.
Chapter 3 Solutions
Essentials of Statistics Books a la carte Plus NEW MyLab Statistics with Pearson eText - Access Card Package (5th Edition)
Ch. 3.2 - Employment Data listed below are results from the...Ch. 3.2 - Average The web site IncomeTaxList.com lists the...Ch. 3.2 - Median In an editorial, the Poughkeepsie Journal...Ch. 3.2 - Prob. 4BSCCh. 3.2 - In Exercises 5-20, find the (a) mean, (b) median,...Ch. 3.2 - In Exercises 5-20, find the (a) mean, (b) median,...Ch. 3.2 - In Exercises 5-20, find the (a) mean, (b) median,...Ch. 3.2 - Prob. 8BSCCh. 3.2 - In Exercises 5-20, find the (a) mean, (b) median,...Ch. 3.2 - Prob. 10BSC
Ch. 3.2 - In Exercises 5-20, find the (a) mean, (b) median,...Ch. 3.2 - In Exercises 5-20, find the (a) mean, (b) median,...Ch. 3.2 - In Exercises 5-20, find the (a) mean, (b) median,...Ch. 3.2 - Prob. 14BSCCh. 3.2 - In Exercises 5-20, find the (a) mean, (b) median,...Ch. 3.2 - In Exercises 5-20, find the (a) mean, (b) median,...Ch. 3.2 - In Exercises 5-20, find the (a) mean, (b) median,...Ch. 3.2 - Prob. 18BSCCh. 3.2 - In Exercises 5-20, find the (a) mean, (b) median,...Ch. 3.2 - In Exercises 5-20, find the (a) mean, (b) median,...Ch. 3.2 - In Exercises 21-24, find the mean and median for...Ch. 3.2 - In Exercises 21-24, find the mean and median for...Ch. 3.2 - Prob. 23BSCCh. 3.2 - In Exercises 21-24, find the mean and median for...Ch. 3.2 - Large Data Sots from Appendix B. In Exercises...Ch. 3.2 - Prob. 26BSCCh. 3.2 - Prob. 27BSCCh. 3.2 - Prob. 28BSCCh. 3.2 - Prob. 29BSCCh. 3.2 - In Exercises 29-32, find the mean of the data...Ch. 3.2 - Prob. 31BSCCh. 3.2 - In Exercises 29-32, find the mean of the data...Ch. 3.2 - Degrees of Freedom Carbon monoxide is measured in...Ch. 3.2 - Prob. 34BBCh. 3.2 - Trimmed Mean Because the mean is very sensitive to...Ch. 3.2 - Prob. 36BBCh. 3.2 - Prob. 37BBCh. 3.2 - Quadratic Mean The quadratic mean (or root mean...Ch. 3.2 - Prob. 39BBCh. 3.3 - Comparing Variation Which do you think has less...Ch. 3.3 - Correct Statements? Which of the following...Ch. 3.3 - Variation and Variance In statistics, how do the...Ch. 3.3 - Prob. 4BSCCh. 3.3 - In Exercises 5-20, find the range, variance, and...Ch. 3.3 - In Exercises 5-20, find the range, variance, and...Ch. 3.3 - Prob. 7BSCCh. 3.3 - In Exercises 5-20, find the range, variance, and...Ch. 3.3 - Prob. 9BSCCh. 3.3 - In Exercises 5-20, find the range, variance, and...Ch. 3.3 - Prob. 11BSCCh. 3.3 - Prob. 12BSCCh. 3.3 - Prob. 13BSCCh. 3.3 - In Exercises 5-20, find the range, variance, and...Ch. 3.3 - Prob. 15BSCCh. 3.3 - In Exercises 5-20, find the range, variance, and...Ch. 3.3 - In Exercises 5-20, find the range, variance, and...Ch. 3.3 - Prob. 18BSCCh. 3.3 - In Exercises 5-20, find the range, variance, and...Ch. 3.3 - In Exercises 5-20, find the range, variance, and...Ch. 3.3 - Prob. 21BSCCh. 3.3 - Prob. 22BSCCh. 3.3 - Prob. 23BSCCh. 3.3 - Prob. 24BSCCh. 3.3 - Prob. 25BSCCh. 3.3 - Prob. 26BSCCh. 3.3 - Prob. 27BSCCh. 3.3 - Prob. 28BSCCh. 3.3 - Prob. 29BSCCh. 3.3 - Estimating Standard Deviation with the Range Rule...Ch. 3.3 - Prob. 31BSCCh. 3.3 - Prob. 32BSCCh. 3.3 - Prob. 33BSCCh. 3.3 - Prob. 34BSCCh. 3.3 - Identifying Unusual Values with the Range Rule of...Ch. 3.3 - Prob. 36BSCCh. 3.3 - Prob. 37BSCCh. 3.3 - Finding Standard Deviation from a Frequency...Ch. 3.3 - Prob. 39BSCCh. 3.3 - Finding Standard Deviation from a Frequency...Ch. 3.3 - Prob. 41BSCCh. 3.3 - The Empirical Rule Based on Data Set 3 Body...Ch. 3.3 - Prob. 43BSCCh. 3.3 - Chebyshev's Theorem Based on Data Set 3 in...Ch. 3.3 - Why Divide by n 1? Let a population consist of...Ch. 3.3 - Prob. 46BBCh. 3.4 - z Scores James Madison, the fourth President of...Ch. 3.4 - Prob. 2BSCCh. 3.4 - Prob. 3BSCCh. 3.4 - Prob. 4BSCCh. 3.4 - Prob. 5BSCCh. 3.4 - Prob. 6BSCCh. 3.4 - Prob. 7BSCCh. 3.4 - Prob. 8BSCCh. 3.4 - Prob. 9BSCCh. 3.4 - Prob. 10BSCCh. 3.4 - Usual and Unusual Values.In Exercises 9-12,...Ch. 3.4 - Usual and Unusual Values.In Exercises 9-12,...Ch. 3.4 - Prob. 13BSCCh. 3.4 - Prob. 14BSCCh. 3.4 - Comparing Values.In Exercises 13-16, use z scores...Ch. 3.4 - Prob. 16BSCCh. 3.4 - Percentiles. In Exercises 17-20, use the following...Ch. 3.4 - Prob. 18BSCCh. 3.4 - Prob. 19BSCCh. 3.4 - Prob. 20BSCCh. 3.4 - Prob. 21BSCCh. 3.4 - Prob. 22BSCCh. 3.4 - Prob. 23BSCCh. 3.4 - Prob. 24BSCCh. 3.4 - Prob. 25BSCCh. 3.4 - Prob. 26BSCCh. 3.4 - Prob. 27BSCCh. 3.4 - Prob. 28BSCCh. 3.4 - Boxplots. In Exercises 29-32, use the given data...Ch. 3.4 - Prob. 30BSCCh. 3.4 - Prob. 31BSCCh. 3.4 - Boxplots. In Exercises 29-32, use the given data...Ch. 3.4 - Prob. 33BSCCh. 3.4 - Boxplots from Larger Data Sets In Appendix B. In...Ch. 3.4 - Prob. 35BSCCh. 3.4 - Boxplots from Larger Data Sets In Appendix B. In...Ch. 3.4 - Prob. 37BBCh. 3.4 - Prob. 38BBCh. 3 - Find the mean of these times that American...Ch. 3 - What is the median of the sample values listed in...Ch. 3 - Prob. 3CQQCh. 3 - The standard deviation of the sample values in...Ch. 3 - The taxi-in times for 48 flights that landed in...Ch. 3 - You plan to investigate the variation of taxi-in...Ch. 3 - Consider a sample taken from the population of all...Ch. 3 - Consider a sample taken from the population of all...Ch. 3 - Approximately what percentage of taxi-in times is...Ch. 3 - Prob. 10CQQCh. 3 - Ergonomics When designing an eye-recognition...Ch. 3 - z Score Using the sample data from Exercise 1,...Ch. 3 - Boxplot Using the same standing heights listed in...Ch. 3 - Prob. 4RECh. 3 - Prob. 5RECh. 3 - Aircraft Design Engineers designing overhead bin...Ch. 3 - Prob. 9RECh. 3 - Moan or Median? A statistics class with 40...Ch. 3 - Designing Gloves An engineer is designing a...Ch. 3 - Frequency Distribution Use the hand lengths in...Ch. 3 - Histogram Use the frequency distribution from...Ch. 3 - Stemplot Use the hand lengths from Exercise 1 to...Ch. 3 - Descriptive Statistics Use the hand lengths in...Ch. 3 - Normal Distribution Instead of using the hand...Ch. 3 - Sampling Shortly after the World Trade Center...Ch. 3 - Prob. 8CRE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- 2. Which of the following statements are (not) true? lim sup{An U Bn} 818 lim sup{A, B} 818 lim inf{An U Bn} 818 818 lim inf{A, B} An An A, Bn- A, BnB →B = = = lim sup A, U lim sup Bn; 818 818 lim sup A, lim sup Bn; 818 81U lim inf A, U lim inf Bn; 818 818 lim inf A, lim inf Bn; n→X 818 An U BRAUB as no; An OBRANB as n→∞.arrow_forwardThroughout, A, B, (An, n≥ 1), and (Bn, n≥ 1) are subsets of 2. 1. Show that AAB (ANB) U (BA) = (AUB) (AB), Α' Δ Β = Α Δ Β, {A₁ U A2} A {B₁ U B2) C (A1 A B₁}U{A2 A B2).arrow_forward16. Show that, if X and Y are independent random variables, such that E|X|< ∞, and B is an arbitrary Borel set, then EXI{Y B} = EX P(YE B).arrow_forward
- Proposition 1.1 Suppose that X1, X2,... are random variables. The following quantities are random variables: (a) max{X1, X2) and min(X1, X2); (b) sup, Xn and inf, Xn; (c) lim sup∞ X and lim inf∞ Xn- (d) If Xn(w) converges for (almost) every w as n→ ∞, then lim- random variable. → Xn is aarrow_forwardExercise 4.2 Prove that, if A and B are independent, then so are A and B, Ac and B, and A and B.arrow_forward8. Show that, if {Xn, n ≥ 1) are independent random variables, then sup X A) < ∞ for some A.arrow_forward
- 8- 6. Show that, for any random variable, X, and a > 0, 8 心 P(xarrow_forward15. This problem extends Problem 20.6. Let X, Y be random variables with finite mean. Show that 00 (P(X ≤ x ≤ Y) - P(X ≤ x ≤ X))dx = E Y — E X.arrow_forward(b) Define a simple random variable. Provide an example.arrow_forward17. (a) Define the distribution of a random variable X. (b) Define the distribution function of a random variable X. (c) State the properties of a distribution function. (d) Explain the difference between the distribution and the distribution function of X.arrow_forward16. (a) Show that IA(w) is a random variable if and only if A E Farrow_forward15. Let 2 {1, 2,..., 6} and Fo({1, 2, 3, 4), (3, 4, 5, 6}). (a) Is the function X (w) = 21(3, 4) (w)+711.2,5,6) (w) a random variable? Explain. (b) Provide a function from 2 to R that is not a random variable with respect to (N, F). (c) Write the distribution of X. (d) Write and plot the distribution function of X.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
The Shape of Data: Distributions: Crash Course Statistics #7; Author: CrashCourse;https://www.youtube.com/watch?v=bPFNxD3Yg6U;License: Standard YouTube License, CC-BY
Shape, Center, and Spread - Module 20.2 (Part 1); Author: Mrmathblog;https://www.youtube.com/watch?v=COaid7O_Gag;License: Standard YouTube License, CC-BY
Shape, Center and Spread; Author: Emily Murdock;https://www.youtube.com/watch?v=_YyW0DSCzpM;License: Standard Youtube License