
MML PRECALCULUS ENHANCED
7th Edition
ISBN: 9780134119250
Author: Sullivan
Publisher: INTER PEAR
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 3.3, Problem 15SB
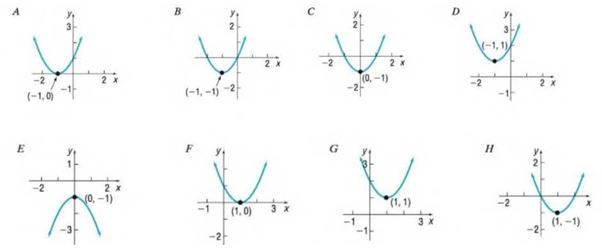
In Problems 13-20, match each graph to one the following functions.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
i need help please
6.
(i)
Sketch the trace of the following curve on R²,
(t) = (sin(t), 3 sin(t)),
tЄ [0, π].
[3 Marks]
Total marks 10
(ii)
Find the length of this curve.
[7 Marks]
helppp
Chapter 3 Solutions
MML PRECALCULUS ENHANCED
Ch. 3.1 - Graph y=2x3 . (pp. 32-35)Ch. 3.1 - Find the slope of the line joining the points (...Ch. 3.1 - Find the average rate of change of f(x)=3 x 2 2 ,...Ch. 3.1 - Solve: 6x900=15x+2850 . (pp. A44-A46)Ch. 3.1 - If f( x )= x 2 4 , find f( 2 ) . (pp. 60-62)Ch. 3.1 - True or False The graph of the function f( x )= x...Ch. 3.1 - For the graph of the linear function f( x )=mx+b ,...Ch. 3.1 - If the slope m of the graph of a linear function...Ch. 3.1 - True or False The slope of a nonvertical line is...Ch. 3.1 - True or False The average rate of change of f( x...
Ch. 3.1 - What is the only type of function that has a...Ch. 3.1 - A car has 12,500 miles on its odometer. Say the...Ch. 3.1 - In Problems 13-20, a linear function is given. a....Ch. 3.1 - In Problems 13-20, a linear function is given. a....Ch. 3.1 - In Problems 13-20, a linear function is given. a....Ch. 3.1 - In Problems 13-20, a linear function is given. a....Ch. 3.1 - In Problems 13-20, a linear function is given. a....Ch. 3.1 - In Problems 13-20, a linear function is given. a....Ch. 3.1 - In Problems 13-20, a linear function is given. a....Ch. 3.1 - In Problems 13-20, a linear function is given. a....Ch. 3.1 - In Problems 21-28, determine whether the given...Ch. 3.1 - In Problems 21-28, determine whether the given...Ch. 3.1 - In Problems 21-28, determine whether the given...Ch. 3.1 - In Problems 21-28, determine whether the given...Ch. 3.1 - In Problems 21-28, determine whether the given...Ch. 3.1 - In Problems 21-28, determine whether the given...Ch. 3.1 - In Problems 21-28, determine whether the given...Ch. 3.1 - In Problems 21-28, determine whether the given...Ch. 3.1 - Suppose that f( x )=4x1 and g(x)=2x+5 . a. Solve...Ch. 3.1 - Suppose that f( x )=3x+5 and g(x)=2x+15 . a. Solve...Ch. 3.1 - In parts (a) - (f), use the following figure. a....Ch. 3.1 - In parts (a) - (f), use the following figure. a....Ch. 3.1 - In parts (a) and (b), use the following figure. a....Ch. 3.1 - In parts (a) and (b), use the following figure. a....Ch. 3.1 - In parts (a) and (b), use the following figure. a....Ch. 3.1 - In parts (a) and (b), use the following figure. a....Ch. 3.1 - Car Rentals The cost C , in dollars, of a one-day...Ch. 3.1 - Phone Charges The monthly cost C , in dollars, for...Ch. 3.1 - Supply and Demand Suppose that the quantity...Ch. 3.1 - Supply and Demand Suppose that the quantity...Ch. 3.1 - Taxes The function T( x )=0.15(x9225)+922.50...Ch. 3.1 - Competitive Balance Tax In 2011, major league...Ch. 3.1 - The point at which a company’s profits equal...Ch. 3.1 - The point at which a company’s profits equal...Ch. 3.1 - Straight-line Depreciation Suppose that a company...Ch. 3.1 - Straight-line Depreciation Suppose that a company...Ch. 3.1 - Cost Function The simplest cost function is the...Ch. 3.1 - Cost Function Refer to Problem 47. Suppose that...Ch. 3.1 - Truck Rentals A truck rental company rents a truck...Ch. 3.1 - International Calling A cell phone company offers...Ch. 3.1 - Developing a Linear Model from Data How many songs...Ch. 3.1 - Developing a Linear Model from Data The following...Ch. 3.1 - Which of the following functions might have the...Ch. 3.1 - Which of the following functions might have the...Ch. 3.1 - Under what circumstances is a linear function f( x...Ch. 3.1 - Explain how the graph of f( x )=mx+b can be used...Ch. 3.1 - Problems 57-60 are based on material teamed...Ch. 3.1 - Problems 57-60 are based on material teamed...Ch. 3.1 - Problems 57-60 are based on material teamed...Ch. 3.1 - Problems 57-60 are based on material teamed...Ch. 3.2 - Plot the points ( 1,5 ),( 2,6 ),( 3,9 ),( 1,12 )...Ch. 3.2 - Find an equation of the line containing the points...Ch. 3.2 - A _____________ is used to help us to see what...Ch. 3.2 - If the Independent variable in a line of best fit...Ch. 3.2 - In Problems 5-10, examine the scatter diagram and...Ch. 3.2 - In Problems 5-10, examine the scatter diagram and...Ch. 3.2 - In Problems 5-10, examine the scatter diagram and...Ch. 3.2 - In Problems 5-10, examine the scatter diagram and...Ch. 3.2 - In Problems 5-10, examine the scatter diagram and...Ch. 3.2 - In Problems 5-10, examine the scatter diagram and...Ch. 3.2 - In Problems 11-16, (a) Draw a scatter diagram. (b)...Ch. 3.2 - In Problems 11-16, (a) Draw a scatter diagram. (b)...Ch. 3.2 - In Problems 11-16, (a) Draw a scatter diagram. (b)...Ch. 3.2 - In Problems 11-16, (a) Draw a scatter diagram. (b)...Ch. 3.2 - In Problems 11-16, (a) Draw a scatter diagram. (b)...Ch. 3.2 - In Problems 11-16, (a) Draw a scatter diagram. (b)...Ch. 3.2 - Candy The following data represent the weight (in...Ch. 3.2 - Tornadoes The following data represent the width...Ch. 3.2 - Video Games and Grade-Point Average Professor...Ch. 3.2 - Hurricanes The following data represent the...Ch. 3.2 - Homeruns A baseball analyst wishes to find a...Ch. 3.2 - Demand for Jeans The marketing manager at...Ch. 3.2 - Maternal Age versus Down Syndrome A biologist...Ch. 3.2 - Find the line of best fit for the ordered pairs (...Ch. 3.2 - What does a correlation coefficient of 0 imply?Ch. 3.2 - Explain why it does not make sense to interpret...Ch. 3.2 - Refer to Problem 19. Solve G( h )=0 . Provide an...Ch. 3.2 - Find an equation for the line containing the...Ch. 3.2 - Find the domain of f( x )= x1 x 2 25 .Ch. 3.2 - For f(x)=5x8 and g(x)= x 2 3x+4 , find (gf)(x) .Ch. 3.2 - Write the function whose graph is the graph of y=...Ch. 3.3 - List the intercepts of the equation y= x 2 9 ....Ch. 3.3 - Prob. 2AYPCh. 3.3 - To complete the square of x 2 5x , you add the...Ch. 3.3 - To graph y= (x4) 2 you shift the graph of y= x 2...Ch. 3.3 - The graph of a quadratic function is called a(n)...Ch. 3.3 - The vertical line passing through the vertex of a...Ch. 3.3 - The x-coordinate of the vertex of f( x )=a x 2...Ch. 3.3 - True or False The graph of f( x )=2 x 2 +3x4 opens...Ch. 3.3 - True or False The y-coordinate of the vertex of f(...Ch. 3.3 - True or False If the discriminant b 2 4ac=0 , the...Ch. 3.3 - If b 2 4ac0 , which of the following conclusions...Ch. 3.3 - If the graph of f( x )=a x 2 +bx+c,a0 , has a...Ch. 3.3 - In Problems 13-20, match each graph to one the...Ch. 3.3 - In Problems 13-20, match each graph to one the...Ch. 3.3 - In Problems 13-20, match each graph to one the...Ch. 3.3 - In Problems 13-20, match each graph to one the...Ch. 3.3 - In Problems 13-20, match each graph to one the...Ch. 3.3 - In Problems 13-20, match each graph to one the...Ch. 3.3 - In Problems 13-20, match each graph to one the...Ch. 3.3 - In Problems 13-20, match each graph to one the...Ch. 3.3 - In Problems 21-32, graph the function f by...Ch. 3.3 - In Problems 21-32, graph the function f by...Ch. 3.3 - In Problems 21-32, graph the function f by...Ch. 3.3 - In Problems 21-32, graph the function f by...Ch. 3.3 - In Problems 21-32, graph the function f by...Ch. 3.3 - In Problems 21-32, graph the function f by...Ch. 3.3 - In Problems 21-32, graph the function f by...Ch. 3.3 - In Problems 21-32, graph the function f by...Ch. 3.3 - In Problems 21-32, graph the function f by...Ch. 3.3 - In Problems 21-32, graph the function f by...Ch. 3.3 - In Problems 21-32, graph the function f by...Ch. 3.3 - In Problems 21-32, graph the function f by...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 33-48, (a) graph each quadratic...Ch. 3.3 - In Problems 49-54, determine the quadratic...Ch. 3.3 - In Problems 49-54, determine the quadratic...Ch. 3.3 - In Problems 49-54, determine the quadratic...Ch. 3.3 - In Problems 49-54, determine the quadratic...Ch. 3.3 - In Problems 49-54, determine the quadratic...Ch. 3.3 - In Problems 49-54, determine the quadratic...Ch. 3.3 - In Problems 55-62, determine, without graphing,...Ch. 3.3 - In Problems 55-62, determine, without graphing,...Ch. 3.3 - In Problems 55-62, determine, without graphing,...Ch. 3.3 - In Problems 55-62, determine, without graphing,...Ch. 3.3 - In Problems 55-62, determine, without graphing,...Ch. 3.3 - In Problems 55-62, determine, without graphing,...Ch. 3.3 - In Problems 55-62, determine, without graphing,...Ch. 3.3 - In Problems 55-62, determine, without graphing,...Ch. 3.3 - In Problems 63-74, (a) graph each function, (b)...Ch. 3.3 - In Problems 63-74, (a) graph each function, (b)...Ch. 3.3 - In Problems 63-74, (a) graph each function, (b)...Ch. 3.3 - In Problems 63-74, (a) graph each function, (b)...Ch. 3.3 - In Problems 63-74, (a) graph each function, (b)...Ch. 3.3 - In Problems 63-74, (a) graph each function, (b)...Ch. 3.3 - In Problems 63-74, (a) graph each function, (b)...Ch. 3.3 - In Problems 63-74, (a) graph each function, (b)...Ch. 3.3 - In Problems 63-74, (a) graph each function, (b)...Ch. 3.3 - In Problems 63-74, (a) graph each function, (b)...Ch. 3.3 - In Problems 63-74, (a) graph each function, (b)...Ch. 3.3 - In Problems 63-74, (a) graph each function, (b)...Ch. 3.3 - The graph of the function f( x )=a x 2 +bx+c has...Ch. 3.3 - The graph of the function f(x)=a x 2 +bx+c has...Ch. 3.3 - In Problems 77-82, for the given functions fandg ,...Ch. 3.3 - In Problems 77-82, for the given functions fandg ,...Ch. 3.3 - In Problems 77-82, for the given functions fandg ,...Ch. 3.3 - In Problems 77-82, for the given functions fandg ,...Ch. 3.3 - In Problems 77-82, for the given functions fandg ,...Ch. 3.3 - In Problems 77-82, for the given functions fandg ,...Ch. 3.3 - Answer Problems 83 and 84 using the following: A...Ch. 3.3 - Answer Problems 83 and 84 using the following: A...Ch. 3.3 - Suppose that f(x)= x 2 +4x21 . (a) What is the...Ch. 3.3 - Suppose that f( x )= x 2 +2x8 . (a) What is the...Ch. 3.3 - Find the point on the line y=x that is closest to...Ch. 3.3 - Find the point on the line y=x+1 that is closest...Ch. 3.3 - Maximizing Revenue Suppose that the manufacturer...Ch. 3.3 - Maximizing Revenue The John Deere company has...Ch. 3.3 - Minimizing Marginal Cost The marginal cost of a...Ch. 3.3 - Minimizing Marginal Cost (See Problem 91.) The...Ch. 3.3 - Business The monthly revenue R achieved by selling...Ch. 3.3 - Business The daily revenue R achieved by selling x...Ch. 3.3 - Stopping Distance An accepted relationship between...Ch. 3.3 - Birthrate for Unmarried Women In the United...Ch. 3.3 - Let f( x )=a x 2 +bx+c , where a,b,andc are odd...Ch. 3.3 - Make up a quadratic function that opens down and...Ch. 3.3 - On one set of coordinate axes, graph the family of...Ch. 3.3 - On one set of coordinate axes, graph the family of...Ch. 3.3 - State the circumstances that cause the graph of a...Ch. 3.3 - Why does the graph of a quadratic function open up...Ch. 3.3 - Can a quadratic function have a range of ( , ) ?...Ch. 3.3 - What are the possibilities for the number of times...Ch. 3.3 - Determine whether x 2 +4 y 2 =16 is symmetric...Ch. 3.3 - Find the domain of f(x)= 82x .Ch. 3.3 - Prob. 107RYKCh. 3.3 - Write the function whose graph is the graph of y=...Ch. 3.4 - Translate the following sentence into a...Ch. 3.4 - Use a graphing utility to find the line of best...Ch. 3.4 - Maximizing Revenue The price p (in dollars) and...Ch. 3.4 - Maximizing Revenue The price p (in dollars) and...Ch. 3.4 - Maximizing Revenue The price p (in dollars) and...Ch. 3.4 - Maximizing Revenue The price p (in dollars) and...Ch. 3.4 - Enclosing a Rectangular Field David has 400 yards...Ch. 3.4 - Enclosing a Rectangular Field Beth has 3000 feet...Ch. 3.4 - Enclosing a Rectangular Field with a Fence A...Ch. 3.4 - Enclosing a Rectangular Field with a Fence A...Ch. 3.4 - Analyzing the Motion of a Projectile A projectile...Ch. 3.4 - Analyzing the Motion of a Projectile A projectile...Ch. 3.4 - Suspension Bridge A suspension bridge with weight...Ch. 3.4 - Architecture A parabolic arch has a span of 120...Ch. 3.4 - Constructing Rain Gutters A rain gutter is to be...Ch. 3.4 - Norman Windows A Norman window has the shape of a...Ch. 3.4 - Constructing a Stadium A track-and-field playing...Ch. 3.4 - Architecture A special window has the shape of a...Ch. 3.4 - Chemical Reactions A self-catalytic chemical...Ch. 3.4 - Calculus: Simpson's Rule The figure shows the...Ch. 3.4 - Use the result obtained in Problem 20 to find the...Ch. 3.4 - Use the result obtained in Problem 20 to find the...Ch. 3.4 - Use the result obtained in Problem 20 to find the...Ch. 3.4 - Use the result obtained in Problem 20 to find the...Ch. 3.4 - Life Cycle Hypothesis An individuals income varies...Ch. 3.4 - Height of a Rail A shot-putter throws a hall at an...Ch. 3.4 - Which Model? The following data represent the...Ch. 3.4 - Which Model? An engineer collects the following...Ch. 3.4 - Which Model? The following data represent the...Ch. 3.4 - Which Model? A cricket makes a chirping noise by...Ch. 3.4 - Refer to Example 1 in this section. Notice that if...Ch. 3.4 - Find an equation of the line containing the points...Ch. 3.4 - Find the distance between the points P 1 =( 4,7 )...Ch. 3.4 - Prob. 34RYKCh. 3.4 - Find the intercepts of the graph of 3 x 2 4y=48 .Ch. 3.5 - Solve the inequality 3x27 .Ch. 3.5 - Write (2,7] using inequality notation.Ch. 3.5 - (a) f( x )0 (b) f( x )0Ch. 3.5 - (a) g( x )0 (b) g( x )0Ch. 3.5 - (a) g( x )f( x ) (b) f( x )g( x )Ch. 3.5 - (a) f( x )g( x ) (b) f( x )g( x )Ch. 3.5 - x 2 3x100Ch. 3.5 - x 2 +3x100Ch. 3.5 - x 2 4x0Ch. 3.5 - x 2 +8x0Ch. 3.5 - x 2 90Ch. 3.5 - x 2 10Ch. 3.5 - x 2 +x12Ch. 3.5 - x 2 +7x12Ch. 3.5 - 2 x 2 5x+3Ch. 3.5 - 6 x 2 6+5xCh. 3.5 - x 2 x+10Ch. 3.5 - x 2 +2x+40Ch. 3.5 - 4 x 2 +96xCh. 3.5 - 25 x 2 +1640xCh. 3.5 - 6( x 2 1 )5xCh. 3.5 - 2( 2 x 2 3x )9Ch. 3.5 - What is the domain of the function f( x )= x 2 16...Ch. 3.5 - What is the domain of the function f( x )= x3 x 2...Ch. 3.5 - In Problems 25-32, use the given functions f and g...Ch. 3.5 - In Problems 25-32, use the given functions f and g...Ch. 3.5 - In Problems 25-32, use the given functions f and g...Ch. 3.5 - In Problems 25-32, use the given functions f and g...Ch. 3.5 - In Problems 25-32, use the given functions f and g...Ch. 3.5 - In Problems 25-32, use the given functions f and g...Ch. 3.5 - In Problems 25-32, use the given functions f and g...Ch. 3.5 - In Problems 25-32, use the given functions f and g...Ch. 3.5 - Physics A ball is thrown vertically upward with an...Ch. 3.5 - Physics A ball is thrown vertically upward with an...Ch. 3.5 - Revenue Suppose that the manufacturer of a gas...Ch. 3.5 - Revenue The John Deere company has found that the...Ch. 3.5 - Artillery A projectile Fired from the point ( 0,0...Ch. 3.5 - Runaway Car Using Hooke's Law, we can show that...Ch. 3.5 - Show that the inequality ( x4 ) 2 0 has exactly...Ch. 3.5 - Show that the inequality ( x2 ) 2 0 has one real...Ch. 3.5 - Explain why the inequality x 2 +x+10 has all real...Ch. 3.5 - Explain why the inequality x 2 x+10 has the empty...Ch. 3.5 - Explain the circumstances under which the...Ch. 3.5 - Determine the domain of f( x )= 102x .Ch. 3.5 - Consider the linear function f( x )= 2 3 x6 . (a)...Ch. 3.5 - Determine algebraically whether f( x )= x x 2 +9...Ch. 3.5 - Determine whether the graphs of 6x3y=10 and 2x+y=8...Ch. 3.R - In Problems 1-3: (a) Determine the slope and...Ch. 3.R - In Problems 1-3: (a) Determine the slope and...Ch. 3.R - In Problems 1-3: (a) Determine the slope and...Ch. 3.R - In Problems 4 and 5, determine whether the...Ch. 3.R - In Problems 4 and 5, determine whether the...Ch. 3.R - In Problems 6-8, graph each quadratic function...Ch. 3.R - In Problems 6-8, graph each quadratic function...Ch. 3.R - In Problems 6-8, graph each quadratic function...Ch. 3.R - In Problems 9-14, (a) graph each quadratic...Ch. 3.R - In Problems 9-14, (a) graph each quadratic...Ch. 3.R - In Problems 9-14, (a) graph each quadratic...Ch. 3.R - In Problems 9-14, (a) graph each quadratic...Ch. 3.R - In Problems 9-14, (a) graph each quadratic...Ch. 3.R - In Problems 9-14, (a) graph each quadratic...Ch. 3.R - In Problems 15-17, determine whether the given...Ch. 3.R - In Problems 15-17, determine whether the given...Ch. 3.R - In Problems 15-17, determine whether the given...Ch. 3.R - In Problems 18-19, solve each quadratic...Ch. 3.R - In Problems 18-19, solve each quadratic...Ch. 3.R - 20. In Problems 20 and 21, find the quadratic...Ch. 3.R - 21. In Problems 20 and 21, find the quadratic...Ch. 3.R - 22. Sales Commissions Bill has just been offered a...Ch. 3.R - 23. Demand Equation the price p (in dollars) and...Ch. 3.R - 24. Enclosing the Most Area with a Fence A farmer...Ch. 3.R - 25. Minimizing Marginal Cost Callaway Golf Company...Ch. 3.R - 26. Maximizing Area A rectangle has one vertex on...Ch. 3.R - 27. Parabolic Arch Bridge A horizontal bridge is...Ch. 3.R - 28. Bono Length Research performed at NASA, led by...Ch. 3.R - 29. Advertising A small manufacturing firm...Ch. 3.CT - For the linear function f( x )=4x+3 , a. Find the...Ch. 3.CT - Determine whether the given function is linear or...Ch. 3.CT - Graph f(x)= (x3) 2 2 using transformations.Ch. 3.CT - In Problems 4 and 5, a. Determine whether the...Ch. 3.CT - In Problems 4 and 5, a. Determine whether the...Ch. 3.CT - Determine the quadratic function for the given...Ch. 3.CT - Determine whether f( x )=-2 x 2 +12x+3 has a...Ch. 3.CT - Solve, x 2 10x+240 .Ch. 3.CT - The weekly rental cost of a 20-foot recreational...Ch. 3.CT - The price p (in dollars) and the quantity x sold...Ch. 3.CT - Consider these two data sets: One data set follows...Ch. 3.CR - Find the distance between the points P=( 1,3 ) and...Ch. 3.CR - Which of the following points are on the graph of,...Ch. 3.CR - Solve the inequality 5x+30 and graph the solution...Ch. 3.CR - Find the equation of the line containing the...Ch. 3.CR - Find the equation of the line perpendicular to the...Ch. 3.CR - Graph the equation x 2 + y 2 4x+8y5=0 .Ch. 3.CR - Does the following relation represent a function?...Ch. 3.CR - For the function f defined by f( x )= x 2 4x+1 ,...Ch. 3.CR - Find the domain of h(z)= 3z1 6z7 .Ch. 3.CR - Is the following graph the graph of a function?Ch. 3.CR - Consider the function f(x)= x x+4 . a. Is the...Ch. 3.CR - Is the function f(x)= x 2 2x+1 even, odd, or...Ch. 3.CR - Approximate the local maximum values and local...Ch. 3.CR - If f(x)=3x+5 and g(x)=2x+1 , a. Solve f(x)=g( x )...Ch. 3.CR - For the graph of the function f , a. Find the...
Additional Math Textbook Solutions
Find more solutions based on key concepts
A categorical variable has three categories, with the following frequencies of occurrence: a. Compute the perce...
Basic Business Statistics, Student Value Edition
CHECK POINT I Express as a percent.
Thinking Mathematically (6th Edition)
Assessment 1-1A Cookies are sold singly or in packages of 2 or 6. With this packaging, how many ways can you bu...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
In Exercises 25–28, use the confidence interval to find the margin of error and the sample mean.
25. (12.0, 14....
Elementary Statistics: Picturing the World (7th Edition)
The table by using the given graph of h.
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 7. Let F(x1, x2) (F₁(x1, x2), F2(x1, x2)), where = X2 F1(x1, x2) X1 F2(x1, x2) x+x (i) Using the definition, calculate the integral LF.dy, where (t) = (cos(t), sin(t)) and t = [0,2]. [5 Marks] (ii) Explain why Green's Theorem cannot be used to find the integral in part (i). [5 Marks]arrow_forward6. Sketch the trace of the following curve on R², п 3п (t) = (t2 sin(t), t2 cos(t)), tЄ 22 [3 Marks] Find the length of this curve. [7 Marks]arrow_forwardTotal marks 10 Total marks on naner: 80 7. Let DCR2 be a bounded domain with the boundary OD which can be represented as a smooth closed curve : [a, b] R2, oriented in the anticlock- wise direction. Use Green's Theorem to justify that the area of the domain D can be computed by the formula 1 Area(D) = ½ (−y, x) · dy. [5 Marks] (ii) Use the area formula in (i) to find the area of the domain D enclosed by the ellipse y(t) = (10 cos(t), 5 sin(t)), t = [0,2π]. [5 Marks]arrow_forward
- Total marks 15 Total marks on paper: 80 6. Let DCR2 be a bounded domain with the boundary ǝD which can be represented as a smooth closed curve : [a, b] → R², oriented in the anticlockwise direction. (i) Use Green's Theorem to justify that the area of the domain D can be computed by the formula 1 Area(D) = . [5 Marks] (ii) Use the area formula in (i) to find the area of the domain D enclosed by the ellipse (t) = (5 cos(t), 10 sin(t)), t = [0,2π]. [5 Marks] (iii) Explain in your own words why Green's Theorem can not be applied to the vector field У x F(x,y) = ( - x² + y²²x² + y² ). [5 Marks]arrow_forwardTotal marks 15 པ་ (i) Sketch the trace of the following curve on R2, (t) = (t2 cos(t), t² sin(t)), t = [0,2π]. [3 Marks] (ii) Find the length of this curve. (iii) [7 Marks] Give a parametric representation of a curve : [0, that has initial point (1,0), final point (0, 1) and the length √2. → R² [5 Marks] Turn over. MA-201: Page 4 of 5arrow_forwardTotal marks 15 5. (i) Let f R2 R be defined by f(x1, x2) = x² - 4x1x2 + 2x3. Find all local minima of f on R². (ii) [10 Marks] Give an example of a function f: R2 R which is not bounded above and has exactly one critical point, which is a minimum. Justify briefly your answer. [5 Marks] 6. (i) Sketch the trace of the following curve on R2, y(t) = (sin(t), 3 sin(t)), t = [0,π]. [3 Marks]arrow_forward
- A ladder 25 feet long is leaning against the wall of a building. Initially, the foot of the ladder is 7 feet from the wall. The foot of the ladder begins to slide at a rate of 2 ft/sec, causing the top of the ladder to slide down the wall. The location of the foot of the ladder, its x coordinate, at time t seconds is given by x(t)=7+2t. wall y(1) 25 ft. ladder x(1) ground (a) Find the formula for the location of the top of the ladder, the y coordinate, as a function of time t. The formula for y(t)= √ 25² - (7+2t)² (b) The domain of t values for y(t) ranges from 0 (c) Calculate the average velocity of the top of the ladder on each of these time intervals (correct to three decimal places): . (Put your cursor in the box, click and a palette will come up to help you enter your symbolic answer.) time interval ave velocity [0,2] -0.766 [6,8] -3.225 time interval ave velocity -1.224 -9.798 [2,4] [8,9] (d) Find a time interval [a,9] so that the average velocity of the top of the ladder on this…arrow_forwardTotal marks 15 3. (i) Let FRN Rm be a mapping and x = RN is a given point. Which of the following statements are true? Construct counterex- amples for any that are false. (a) If F is continuous at x then F is differentiable at x. (b) If F is differentiable at x then F is continuous at x. If F is differentiable at x then F has all 1st order partial (c) derivatives at x. (d) If all 1st order partial derivatives of F exist and are con- tinuous on RN then F is differentiable at x. [5 Marks] (ii) Let mappings F= (F1, F2) R³ → R² and G=(G1, G2) R² → R² : be defined by F₁ (x1, x2, x3) = x1 + x², G1(1, 2) = 31, F2(x1, x2, x3) = x² + x3, G2(1, 2)=sin(1+ y2). By using the chain rule, calculate the Jacobian matrix of the mapping GoF R3 R², i.e., JGoF(x1, x2, x3). What is JGOF(0, 0, 0)? (iii) [7 Marks] Give reasons why the mapping Go F is differentiable at (0, 0, 0) R³ and determine the derivative matrix D(GF)(0, 0, 0). [3 Marks]arrow_forward5. (i) Let f R2 R be defined by f(x1, x2) = x² - 4x1x2 + 2x3. Find all local minima of f on R². (ii) [10 Marks] Give an example of a function f: R2 R which is not bounded above and has exactly one critical point, which is a minimum. Justify briefly Total marks 15 your answer. [5 Marks]arrow_forward
- Total marks 15 4. : Let f R2 R be defined by f(x1, x2) = 2x²- 8x1x2+4x+2. Find all local minima of f on R². [10 Marks] (ii) Give an example of a function f R2 R which is neither bounded below nor bounded above, and has no critical point. Justify briefly your answer. [5 Marks]arrow_forward4. Let F RNR be a mapping. (i) x ЄRN ? (ii) : What does it mean to say that F is differentiable at a point [1 Mark] In Theorem 5.4 in the Lecture Notes we proved that if F is differentiable at a point x E RN then F is continuous at x. Proof. Let (n) CRN be a sequence such that xn → x ЄERN as n → ∞. We want to show that F(xn) F(x), which means F is continuous at x. Denote hnxn - x, so that ||hn|| 0. Thus we find ||F(xn) − F(x)|| = ||F(x + hn) − F(x)|| * ||DF (x)hn + R(hn) || (**) ||DF(x)hn||+||R(hn)||| → 0, because the linear mapping DF(x) is continuous and for all large nЄ N, (***) ||R(hn) || ||R(hn) || ≤ → 0. ||hn|| (a) Explain in details why ||hn|| → 0. [3 Marks] (b) Explain the steps labelled (*), (**), (***). [6 Marks]arrow_forward4. In Theorem 5.4 in the Lecture Notes we proved that if F: RN → Rm is differentiable at x = RN then F is continuous at x. Proof. Let (xn) CRN be a sequence such that x → x Є RN as n → ∞. We want F(x), which means F is continuous at x. to show that F(xn) Denote hn xnx, so that ||hn||| 0. Thus we find ||F (xn) − F(x) || (*) ||F(x + hn) − F(x)|| = ||DF(x)hn + R(hn)|| (**) ||DF(x)hn|| + ||R(hn) || → 0, because the linear mapping DF(x) is continuous and for all large n = N, |||R(hn) || ≤ (***) ||R(hn)|| ||hn|| → 0. Explain the steps labelled (*), (**), (***) [6 Marks] (ii) Give an example of a function F: RR such that F is contin- Total marks 10 uous at x=0 but F is not differentiable at at x = 0. [4 Marks]arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning

Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning

Intermediate Algebra
Algebra
ISBN:9781285195728
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning

Algebraic Complexity with Less Relations; Author: The University of Chicago;https://www.youtube.com/watch?v=ZOKM1JPz650;License: Standard Youtube License
Strassen's Matrix Multiplication - Divide and Conquer - Analysis of Algorithm; Author: Ekeeda;https://www.youtube.com/watch?v=UnpySHwAJsQ;License: Standard YouTube License, CC-BY
Trigonometric Equations with Complex Numbers | Complex Analysis #6; Author: TheMathCoach;https://www.youtube.com/watch?v=zdD8Dab1T2Y;License: Standard YouTube License, CC-BY