
Concept explainers
Applications.
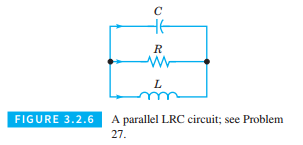
Electric Circuits. The theory of electric circuits, such as that shown in Figure 3.2.6, consisting of inductors, resistors, and capacitors, is based on Kirchhoff’s laws: (1) At any node (or junction), the sum of currents flowing into that node is equal to the sum of currents flowing into that node is equal to the sum of currents flowing out of that node, and (2) the net voltage drop around each closed loop is zero. In addition to Kirchhoff’s laws, we also have the relation between the current
Kirchhoff’s laws and the current-voltage relation for each circuit element provide a system of algebraic and differential equations from which the voltage and current throughout the circuit can be determined. Problems 27 through 29 illustrate the procedure just described.
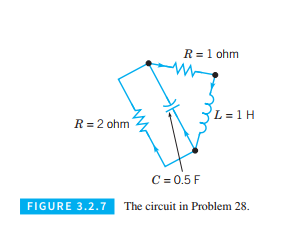
Consider the circuit shown in the Figure 3.2.7. Use the method outlined in problem 27 to show that the current
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
DIFFERENTIAL EQUATIONS(LL) W/WILEYPLUS
Additional Math Textbook Solutions
Pre-Algebra Student Edition
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Probability And Statistical Inference (10th Edition)
Elementary Statistics Using The Ti-83/84 Plus Calculator, Books A La Carte Edition (5th Edition)
Algebra and Trigonometry (6th Edition)
- use a graphing utility to sketch the graph of the function and then use the graph to help identify or approximate the domain and range of the function. f(x)=xsqrt(9-(x^2))arrow_forward4. Select all of the solutions for x²+x - 12 = 0? A. -12 B. -4 C. -3 D. 3 E 4 F 12 4 of 10arrow_forward2. Select all of the polynomials with the degree of 7. A. h(x) = (4x + 2)³(x − 7)(3x + 1)4 B h(x) = (x + 7)³(2x + 1)^(6x − 5)² ☐ Ch(x)=(3x² + 9)(x + 4)(8x + 2)ª h(x) = (x + 6)²(9x + 2) (x − 3) h(x)=(-x-7)² (x + 8)²(7x + 4)³ Scroll down to see more 2 of 10arrow_forward
- 1. If all of the zeros for a polynomial are included in the graph, which polynomial could the graph represent? 100 -6 -2 0 2 100 200arrow_forward3. Select the polynomial that matches the description given: Zero at 4 with multiplicity 3 Zero at −1 with multiplicity 2 Zero at -10 with multiplicity 1 Zero at 5 with multiplicity 5 ○ A. P(x) = (x − 4)³(x + 1)²(x + 10)(x — 5)³ B - P(x) = (x + 4)³(x − 1)²(x − 10)(x + 5)³ ○ ° P(x) = (1 − 3)'(x + 2)(x + 1)"'" (x — 5)³ 51 P(r) = (x-4)³(x − 1)(x + 10)(x − 5 3 of 10arrow_forwardMatch the equation, graph, and description of transformation. Horizontal translation 1 unit right; vertical translation 1 unit up; vertical shrink of 1/2; reflection across the x axis Horizontal translation 1 unit left; vertical translation 1 unit down; vertical stretch of 2 Horizontal translation 2 units right; reflection across the x-axis Vertical translation 1 unit up; vertical stretch of 2; reflection across the x-axis Reflection across the x - axis; vertical translation 2 units down Horizontal translation 2 units left Horizontal translation 2 units right Vertical translation 1 unit down; vertical shrink of 1/2; reflection across the x-axis Vertical translation 2 units down Horizontal translation 1 unit left; vertical translation 2 units up; vertical stretch of 2; reflection across the x - axis f(x) = - =-½ ½ (x − 1)²+1 f(x) = x²-2 f(x) = -2(x+1)²+2 f(x)=2(x+1)²-1 f(x)=-(x-2)² f(x)=(x-2)² f(x) = f(x) = -2x²+1 f(x) = -x²-2 f(x) = (x+2)²arrow_forward
- What is the vertex, increasing interval, decreasing interval, domain, range, root/solution/zero, and the end behavior?arrow_forwardCalculate a (bxc) where a = i, b = j, and c = k.arrow_forwardi+2j+3k = (1,2,3) and b = -i-k. Calculate the cross product a x b where a Next calculate the area of the parallelogram spanned by a and b.arrow_forward
- The measured receptance data around two resonant picks of a structure are tabulated in the followings. Find the natural frequencies, damping ratios, and mode shapes of the structure. (30 points) (@)×10 m/N α₁₂ (@)×10 m/N w/2z (Hz) 99 0.1176 0.17531 0.1114 -0.1751i 101 -0.0302 0.2456i -0.0365 -0.2453i 103 -0.1216 0.1327i -0.1279-0.1324i 220 0.0353 0.0260i -0.0419+0.0259i 224 0.0210 0.0757i |-0.0273 +0.0756i 228 -0.0443 0.0474i 0.0382 +0.0474iarrow_forwardQ3: Define the linear functional J: H(2) R by 1(v) = a(v. v) - L(v) Let u be the unique weak solution to a(u,v) = L(v) in H() and suppose that a(...) is a symmetric bilinear form on H(2) prove that 1- u is minimizer. 2- u is unique. 3- The minimizer J(u,) can be rewritten under algebraic form u Au-ub. J(u)=u'Au- Where A. b are repictively the stiffence matrix and the load vectorarrow_forward== 1. A separable differential equation can be written in the form hy) = g(a) where h(y) is a function of y only, and g(x) is a function of r only. All of the equations below are separable. Rewrite each of these in the form h(y) = g(x), then find a general solution by integrating both sides. Determine whether the solutions you found are explicit (functions) or implicit (curves but not functions) (a) 1' = — 1/3 (b) y' = = --- Y (c) y = x(1+ y²)arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning  Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell



