
Concept explainers
Middle-Level Manager Salaries. Suppose that an independent study of middle-level managers employed at companies located in Atlanta, Georgia, was conducted to compare the salaries of managers working at firms in Atlanta to the salaries of middle-level managers across the nation. The following data show the salary, in thousands of dollars, for a sample of 15 middle-level managers employed at companies in the Atlanta area.

- a. Compute the
median salary for the sample of 15 middle-level managers. Suppose the median salary of middle-level managers employed at companies located across the nation is $85,000. How does the median salary for middle-level managers in the Atlanta area compare to the median for managers across the nation? - b. Compute the
mean annual salary for managers in the Atlanta area and discuss how and why it differs from the median computed in part (a) for Atlanta area managers. - c. Compute the first and third
quartiles for the salaries of middle-level managers in the Atlanta area.
a.
Find the median salary for the sample of 15 middle-level managers.
Compare the median obtained median with the median reported by Wall Street Journal.
Answer to Problem 8E
The median salary for the sample of 15 middle- level managers is $80,000.
Explanation of Solution
Calculation:
The data set represent the salary (in thousand dollars) for a sample of 15 middle-level managers.
Software Procedure:
Step by step procedure to obtain the descriptive statistics using EXCEL is as follows:
- In an EXCEL sheet enter 15 salaries and label it as Salary.
- Go to Data > Data Analysis (in case it is not default, take the Analysis ToolPak from Excel Add Ins) > Descriptive statistics.
- Enter Input Range as $A$2:$A$15, select Columns in Grouped By, tick on Summary statistics.
- Click on OK.
Output using EXCEL is given as follows:
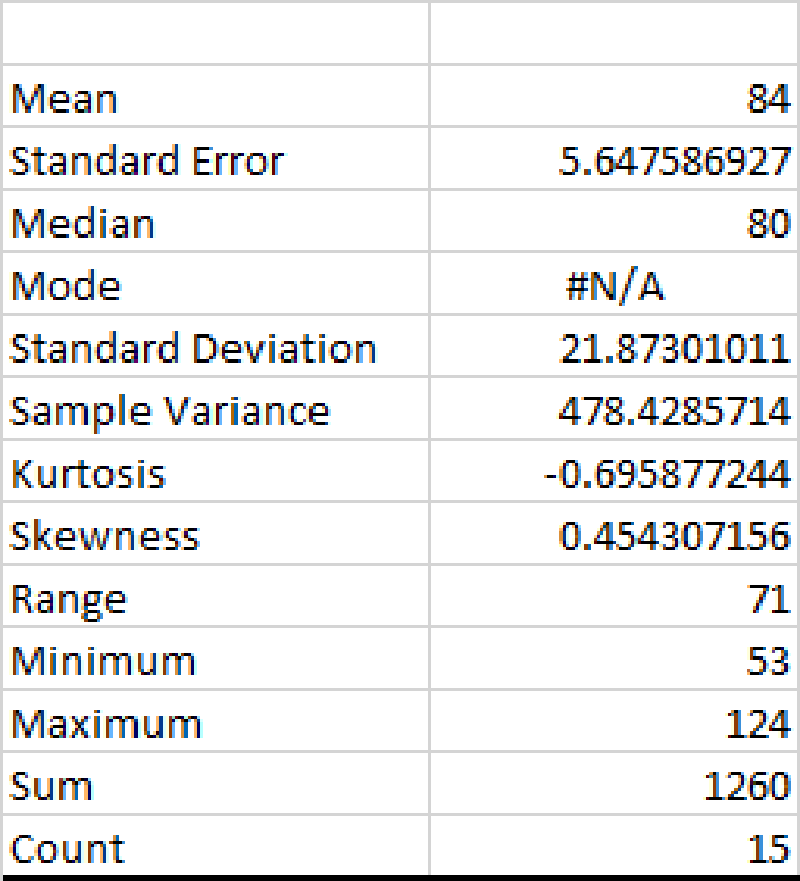
From the EXCEL output, the median salary is 80.
Since, the salary is given in thousand dollars, the median salary for a sample of 15 level managers can be inferred as $80,000.
The Wall Street Journal reported that the median salary for middle-level manager jobs is approximately $85,000.
Here, $80,000 < $85,000.
Therefore, the median salary for the sample of 15 middle-level managers working at firms in City A is slightly lower than the median salary reported by the Wall Street Journal.
b.
Find the mean annual salary.
Explain the reason behind the existence of difference between computed mean and median in part (a).
Answer to Problem 8E
The mean annual salary is $84,000.
The distribution of salaries for middle-level managers working at firms in City A is right skewed.
Explanation of Solution
From the excel output, it is clear that the mean annual salary is 84.
Here, the median salary is less than the mean salary for the sample of 15 middle- level managers.
Skewness:
In statistics, skewness is a measure by which anyone can measure the asymmetrical behaviour of a distribution.
A distribution is said to be symmetric, when its mean, median, and mode are the same. In other words it can be said that, the length of the curve of the left-hand tail will be a mirror image of the right-hand tail.
Therefore, the shape of a distribution can be identified by using the measure of skewness.
Left-skewed:
For a left-skewed distribution,
Right-skewed:
For a right-skewed distribution,
Since, mean is greater than median, it can be inferred that the distribution of annual salary is right or positive skewed.
d.
Obtain the first and third quartiles of the dataset.
Answer to Problem 8E
The first and third quartiles of the dataset are
Explanation of Solution
Calculation:
Quartiles:
Quartiles are those values which divide the data into four equal parts.
Quartiles tells that 25% of the values will be less than the first quartile and 25% of the values will be greater than the third quartile and 50% of the values lies between the first and third quartile with median dividing the parts.
The general formula to obtain the location of
First quartile:
The first quartile
Therefore, the first quartile is the 25th percentile.
The location of 25th percentile is calculated as follows:
Thus, the location of 25th percentile is 4.0.
From this it can be said that, the 25th percentile is 0% of the way between the value in 4th position of ordered dataset and the value in 5th position of ordered dataset.
The dataset of annual salary have to be arranged in ascending order.
The values corresponding to 4th and 5th positions of ordered dataset of annual salaries are 67 and 73.
The 25th percentile is the value in 4th position (67) plus 0.0 times the difference between the value in 4th position and 5th position.
The 25th percentile is obtained as given below:
Hence, the 25th percentile or first quartile is 67.
Third quartile:
The third quartile
Therefore, the third quartile is the 75th percentile.
The location of 75th percentile is calculated as follows:
Thus, the location of 75th percentile is 12.
From this it can be said that, the 75th percentile is 0% of the way between the value in 12th position of ordered dataset and the value in 13th position of ordered dataset.
The dataset of annual salary have to be arranged in ascending order.
The values corresponding to 12th and 13th positions of ordered dataset of annual salaries are 106 and 108.
The 75th percentile is the value in 12th position (106) plus 0.0 times the difference between the value in 12th position and 13th position.
The 75th percentile is obtained as given below:
Hence, the 75th percentile or third quartile is 106.
Thus, the first and third quartiles of the dataset are
Want to see more full solutions like this?
Chapter 3 Solutions
Modern Business Statistics with Microsoft Office Excel (with XLSTAT Education Edition Printed Access Card)
- 9. The concentration function of a random variable X is defined as Qx(h) = sup P(x ≤ X ≤x+h), h>0. Show that, if X and Y are independent random variables, then Qx+y (h) min{Qx(h). Qr (h)).arrow_forward10. Prove that, if (t)=1+0(12) as asf->> O is a characteristic function, then p = 1.arrow_forward9. The concentration function of a random variable X is defined as Qx(h) sup P(x ≤x≤x+h), h>0. (b) Is it true that Qx(ah) =aQx (h)?arrow_forward
- 3. Let X1, X2,..., X, be independent, Exp(1)-distributed random variables, and set V₁₁ = max Xk and W₁ = X₁+x+x+ Isk≤narrow_forward7. Consider the function (t)=(1+|t|)e, ER. (a) Prove that is a characteristic function. (b) Prove that the corresponding distribution is absolutely continuous. (c) Prove, departing from itself, that the distribution has finite mean and variance. (d) Prove, without computation, that the mean equals 0. (e) Compute the density.arrow_forward1. Show, by using characteristic, or moment generating functions, that if fx(x) = ½ex, -∞0 < x < ∞, then XY₁ - Y2, where Y₁ and Y2 are independent, exponentially distributed random variables.arrow_forward
- 1. Show, by using characteristic, or moment generating functions, that if 1 fx(x): x) = ½exarrow_forward1990) 02-02 50% mesob berceus +7 What's the probability of getting more than 1 head on 10 flips of a fair coin?arrow_forward9. The concentration function of a random variable X is defined as Qx(h) sup P(x≤x≤x+h), h>0. = x (a) Show that Qx+b(h) = Qx(h).arrow_forward
- Suppose that you buy a lottery ticket, and you have to pick six numbers from 1 through 50 (repetitions allowed). Which combination is more likely to win: 13, 48, 17, 22, 6, 39 or 1, 2, 3, 4, 5, 6? barrow_forward2 Make a histogram from this data set of test scores: 72, 79, 81, 80, 63, 62, 89, 99, 50, 78, 87, 97, 55, 69, 97, 87, 88, 99, 76, 78, 65, 77, 88, 90, and 81. Would a pie chart be appropriate for this data? ganizing Quantitative Data: Charts and Graphs 45arrow_forward10 Meteorologists use computer models to predict when and where a hurricane will hit shore. Suppose they predict that hurricane Stat has a 20 percent chance of hitting the East Coast. a. On what info are the meteorologists basing this prediction? b. Why is this prediction harder to make than your chance of getting a head on your next coin toss? U anoiaarrow_forward
 Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL


