
Concept explainers
a)
To find: the composite function
a)
Answer to Problem 7E
Explanation of Solution
Given Information:
Three sets are given as
Formula used:
Composition function of two sets R and S can be evaluated as
where x denote the domain of S and y denote the domain of R
Composition function of three sets R , S , and T can be evaluated as
where x is the domain of T and y is the domain of S and z is the domain of R
Calculation:
Consider the set R .
Here in the pair
Consider the set S .
Here in the pair
Construct the following diagram for the relation.
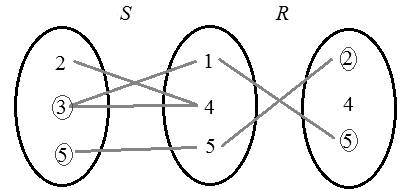
Hence,
b)
To find: the composite function
b)
Answer to Problem 7E
Explanation of Solution
Given Information:
Three sets are given as
Formula used:
Composition function of two sets R and S can be evaluated as
where x denote the domain of S and y denote the domain of R
Composition function of three sets R , S , and T can be evaluated as
where x is the domain of T and y is the domain of S and z is the domain of R
Calculation:
Consider the set R .
Here in the pair
Consider the set T .
Construct the following diagram for the relation.

Hence,
(c)
To find: the composite function
(c)
Answer to Problem 7E
Explanation of Solution
Given Information:
Three sets are given as
Formula used:
Composition function of two sets R and S can be evaluated as
where x denote the domain of S and y denote the domain of R
Composition function of three sets R , S , and T can be evaluated as
where x is the domain of T and y is the domain of S and z is the domain of R
Calculation:
Consider the set S .
Here in the pair
Consider the set T .
Construct the following diagram for the relation.
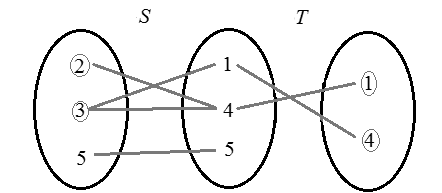
Hence,
(d)
To find: the composite function
(d)
Answer to Problem 7E
Explanation of Solution
Given Information:
Three sets are given as
Formula used:
Composition function of two sets R and S can be evaluated as
where x denote the domain of S and y denote the domain of R
Composition function of three sets R , S , and T can be evaluated as
where x is the domain of T and y is the domain of S and z is the domain of R
Calculation:
Consider the set R .
Here in the pair
Construct the following diagram for the relation.
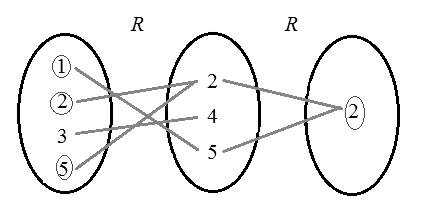
Hence,
(e)
To find: the composite function
(e)
Answer to Problem 7E
Explanation of Solution
Given Information:
Three sets are given as
Formula used:
Composition function of two sets R and S can be evaluated as
where x denote the domain of S and y denote the domain of R
Composition function of three sets R , S , and T can be evaluated as
where x is the domain of T and y is the domain of S and z is the domain of R
Calculation:
Consider the set R .
Here in the pair
Consider the set S .
Here in the pair
Construct the following diagram for the relation.
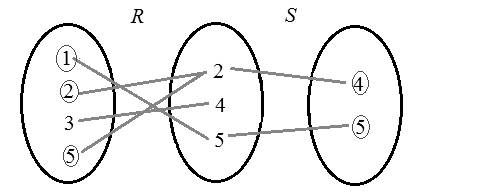
Hence,
(f)
To find: the composite function
(f)
Answer to Problem 7E
Explanation of Solution
Given Information:
Three sets are given as
Formula used:
Composition function of two sets R and S can be evaluated as
where x denote the domain of S and y denote the domain of R
Composition function of three sets R , S , and T can be evaluated as
where x is the domain of T and y is the domain of S and z is the domain of R
Calculation:
Consider the set T .
Construct the following diagram for the relation.
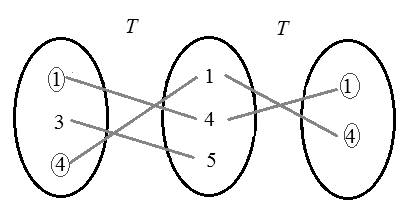
Hence,
(g)
To find: the composite function
(g)
Answer to Problem 7E
Explanation of Solution
Given Information:
Three sets are given as
Formula used:
Composition function of two sets R and S can be evaluated as
where x denote the domain of S and y denote the domain of R
Composition function of three sets R , S , and T can be evaluated as
where x is the domain of T and y is the domain of S and z is the domain of R
Calculation:
Consider the set R .
Here in the pair
Consider the set S .
Here in the pair
Consider the set T .
Construct the following diagram for the relation.

Now, find
Construct the following diagram for the relation.
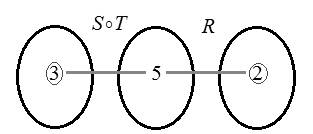
Hence,
(h)
To find: the composite function
(h)
Answer to Problem 7E
Explanation of Solution
Given Information:
Three sets are given as
Formula used:
Composition function of two sets R and S can be evaluated as
where x denote the domain of S and y denote the domain of R
Composition function of three sets R , S , and T can be evaluated as
where x is the domain of T and y is the domain of S and z is the domain of R
Calculation:
Consider the set R .
Here in the pair
Consider the set S .
Here in the pair
Consider the set T .
Construct the following diagram for the relation.
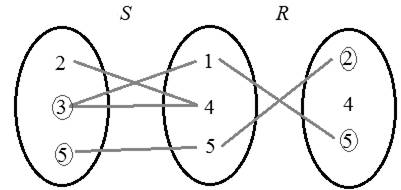
Hence,
Now, find
Construct the following diagram for the relation.
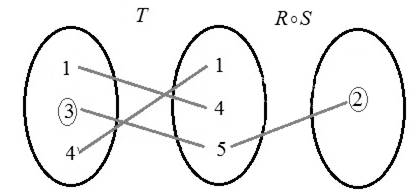
Hence,
Want to see more full solutions like this?
Chapter 3 Solutions
A Transition to Advanced Mathematics
- b) Solve the following linear program using the 2-phase simplex algorithm. You should give the initial tableau, and each further tableau produced during the execution of the algorithm. If the program has an optimal solution, give this solution and state its objective value. If it does not have an optimal solution, say why. maximize ₁ - 2x2+x34x4 subject to 2x1+x22x3x41, 5x1 + x2-x3-×4 ≤ −1, 2x1+x2-x3-34 2, 1, 2, 3, 40.arrow_forward9. An elementary single period market model contains a risk-free asset with interest rate r = 5% and a risky asset S which has price 30 at time t = 0 and will have either price 10 or 60 at time t = 1. Find a replicating strategy for a contingent claim with payoff h(S₁) = max(20 - S₁, 0) + max(S₁ — 50, 0). Total [8 Marks]arrow_forward8. An elementary single period market model has a risky asset with price So = 20 at the beginning and a money market account with interest rate r = 0.04 compounded only once at the end of the investment period. = = In market model A, S₁ 10 with 15% probability and S₁ 21 with 85% probability. In market model B, S₁ = 25 with 10% probability and S₁ = 30 with 90% probability. For each market model A, B, determine if the model is arbitrage-free. If not, construct an arbitrage. Total [9 Marks]arrow_forward
- b) Solve the following linear program using the 2-phase simplex algorithm. You should give the initial tableau, and each further tableau produced during the execution of the algorithm. If the program has an optimal solution, give this solution and state its objective value. If it does not have an optimal solution, say why. maximize ₁ - 2x2+x34x4 subject to 2x1+x22x3x41, 5x1 + x2-x3-×4 ≤ −1, 2x1+x2-x3-34 2, 1, 2, 3, 40.arrow_forwardSuppose we have a linear program in standard equation form maximize cTx subject to Ax = b. x ≥ 0. and suppose u, v, and w are all optimal solutions to this linear program. (a) Prove that zu+v+w is an optimal solution. (b) If you try to adapt your proof from part (a) to prove that that u+v+w is an optimal solution, say exactly which part(s) of the proof go wrong. (c) If you try to adapt your proof from part (a) to prove that u+v-w is an optimal solution, say exactly which part(s) of the proof go wrong.arrow_forwarda) Suppose that we are carrying out the 1-phase simplex algorithm on a linear program in standard inequality form (with 3 variables and 4 constraints) and suppose that we have reached a point where we have obtained the following tableau. Apply one more pivot operation, indicating the highlighted row and column and the row operations you carry out. What can you conclude from your updated tableau? x1 x2 x3 81 82 83 84 81 -2 0 1 1 0 0 0 3 82 3 0 -2 0 1 2 0 6 12 1 1 -3 0 0 1 0 2 84 -3 0 2 0 0 -1 1 4 -2 -2 0 11 0 0-4 0 -8arrow_forward
- Please solve number 2.arrow_forwardConstruct a know-show table of the proposition: For each integer n, n is even if and only if 4 divides n^2arrow_forwardIn Problems 1 and 2 find the eigenfunctions and the equation that defines the eigenvalues for the given boundary-value problem. Use a CAS to approximate the first four eigenvalues A1, A2, A3, and A4. Give the eigenfunctions corresponding to these approximations. 1. y" + Ay = 0, y'(0) = 0, y(1) + y'(1) = 0arrow_forward
- Find the closed formula for each of the following sequences (a_n)_n>=1 by realting them to a well known sequence. Assume the first term given is a_1 d. 5,23,119,719,5039 i have tried finding the differnces and the second difference and i still dont see the patternarrow_forwardYou manage a chemical company with 2 warehouses. The following quantities of Important Chemical A have arrived from an international supplier at 3 different ports: Chemical Available (L) Port 1 Port 2 Port 3 400 110 100 The following amounts of Important Chemical A are required at your warehouses: Warehouse 1 Warehouse 2 Chemical Required (L) 380 230 The cost in £ to ship 1L of chemical from each port to each warehouse is as follows: Warehouse 1 Warehouse 2 Port 1 £10 £45 Port 2 £20 £28 Port 3 £13 £11 (a) You want to know how to send these shipments as cheaply as possible. For- mulate this as a linear program (you do not need to formulate it in standard inequality form) indicating what each variable represents.arrow_forwarda) Suppose that we are carrying out the 1-phase simplex algorithm on a linear program in standard inequality form (with 3 variables and 4 constraints) and suppose that we have reached a point where we have obtained the following tableau. Apply one more pivot operation, indicating the highlighted row and column and the row operations you carry out. What can you conclude from your updated tableau? x1 12 23 81 82 83 S4 $1 -20 1 1 0 0 0 3 82 3 0 -2 0 1 2 0 6 12 1 1 -3 0 0 1 0 2 84 -3 0 2 0 0 -1 1 4 2 -2 0 11 0 0 -4 0 -8 b) Solve the following linear program using the 2-phase simplex algorithm. You should give the initial tableau and each further tableau produced during the execution of the algorithm. If the program has an optimal solution, give this solution and state its objective value. If it does not have an optimal solution, say why. maximize 21 - - 2x2 + x3 - 4x4 subject to 2x1+x22x3x4≥ 1, 5x1+x2-x3-4 -1, 2x1+x2-x3-342, 1, 2, 3, 4 ≥0.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning, Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell 
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning




