Precalculus (6th Edition)
Precalculus (6th Edition)
6th Edition
ISBN: 9780134469140
Author: Robert F. Blitzer
Publisher: PEARSON
bartleby

Videos

Textbook Question
Book Icon
Chapter 3.1, Problem 74PE

Use a calculator with an e x key to solve Exercises 71-76.

The bar graph shows the percentage of U.S. high school seniors who applied to more than three colleges for selected years from 1980 through 2013.

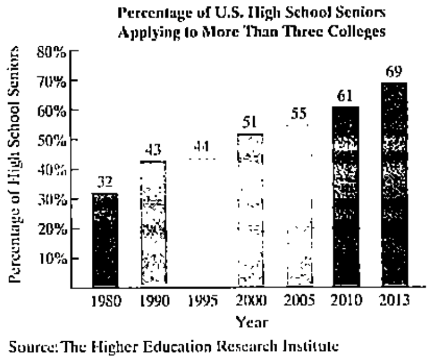
Chapter 3.1, Problem 74PE, Use a calculator with an ex key to solve Exercises 71-76. The bar graph shows the percentage of U.S. , example 1

The data can be modeled by

f ( x ) = x + 31  and  g ( x ) = 32 ⋅ 7 e 0 ⋅ 0217 x ,

in which f(x) and g(x) represent the percentage of high school seniors who applied to more than three colleges x years after 1980. Use these functions to solve Exercises 71-72. Where necessary, round answers to the nearest percent.

In 1626, Peter Minuit convinced the Wappinger Indians to sell him Manhattan Island for $24. If the Native Americans had put the $24 into a bank account paying 5% interest. How much would the investment have been worth in the year 2010 if interest were compounded?

a. monthly? b. continuously?

The bar graph shows the percentage of people 25 years of age and older who were college graduates in the United States for eight selected years.

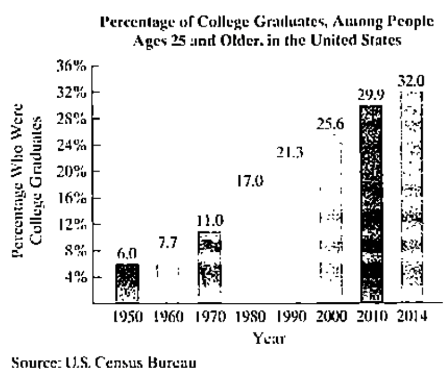
Chapter 3.1, Problem 74PE, Use a calculator with an ex key to solve Exercises 71-76. The bar graph shows the percentage of U.S. , example 2

The functions

f ( x ) = 6 ⋅ 43 ( 1 ⋅ 027 ) r and g ( x ) = 40 ⋅ 9 1 + 6 ⋅ 6 e − 0 ⋅ 049 x

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 3.1, Problem 73PE
Next
Chapter 3.1, Problem 75PE
Students have asked these similar questions
I used a function to model data from 1990 through 2015. The independent variable in my model represented the number of years after 1990, so the function’s domain was {x| x = 0, 1, 2, 3, ......, 25}.Determine whether the statement makes sense or does not make sense, and explain your reasoning.
A house painter has found that the number of job that he has each year is decreasing with respect to the number of years he has been in business. The number of jobs he has each year can be modeled as 104.35 jobs j(x) = X where x is the number of years since 2004. The painter has kept records of the average amount he was paid for each job. His income per job is presented in the table. Average Income per Job Year 2004 2005 2006 2007 2008 2009 2010 Income (dollars) 430 559 727 945 1228 1597 2075 (a) Fill in the blanks to complete an exponential model for average income per job, p, with input x aligned to years since 2004. (Remember to paste the unrounded function model into your calculator before reporting the answer with all numerical values rounded to three decimal places.) p(x) = dollars per job gives the average amount the painter was paid per job x years since 2004✓ ✔ . 0≤x≤6 (b) The equation for the painter's annual income is t(x) = [j(x)p(x) ✔ dollars. (c) Using the unrounded…
Create multiple representations (x-> y table, graph, and equation) of the function g(x)= 2/x. Then make at least 3 summary statements.

Chapter 3 Solutions

Precalculus (6th Edition)

Ch. 3.1 - Check Point 1 Use the exponential function in...Ch. 3.1 - Check Point 2 Graph: Ch. 3.1 - Prob. 3CPCh. 3.1 - Check Point 4 Use the graph of f(x)=3x to obtain...Ch. 3.1 - Prob. 5CPCh. 3.1 - Check Point 6 Use f(x)=1145e00325x, the model...Ch. 3.1 - Prob. 7CPCh. 3.1 - Prob. 1CVCCh. 3.1 - 2. The graph of the exponential function f with...Ch. 3.1 - The value that (1+1n)n approaches as n gets larger...
Ch. 3.1 - 4. Consider the compound interest formula . This...Ch. 3.1 - If compound interest is paid twice a year, we say...Ch. 3.1 - In Exercises 1—10, approximate each number using a...Ch. 3.1 - In Exercises 1-10, approximate each number using a...Ch. 3.1 - In Exercises 1-10, approximate each number using a...Ch. 3.1 - In Exercises 1-10, approximate each number using a...Ch. 3.1 - In Exercises 1-10, approximate each number using a...Ch. 3.1 - In Exercises 1-10, approximate each number using a...Ch. 3.1 - In Exercises 1-10, approximate each number using a...Ch. 3.1 - In Exercises 1-10, approximate each number using a...Ch. 3.1 - In Exercises 1-10, approximate each number using a...Ch. 3.1 - In Exercises 1-10, approximate each number using a...Ch. 3.1 - In Exercises 11-I8, graph each function by making...Ch. 3.1 - In Exercises 11-18, graph each function by making...Ch. 3.1 - In Exercises 11-18, graph each function by making...Ch. 3.1 - In Exercises 11-18, graph each function by making...Ch. 3.1 - In Exercises 11-18, graph each function by making...Ch. 3.1 - In Exercises 11-18, graph each function by making...Ch. 3.1 - In Exercises 11-18, graph each function by making...Ch. 3.1 - In Exercises 11-18,graph each function by making a...Ch. 3.1 - In Exercises 19-24, the graph of an exponential...Ch. 3.1 - In Exercises 19-24, the graph of an exponential...Ch. 3.1 - In Exercises 19-24, the graph of an exponential...Ch. 3.1 - In Exercises 19-24, the graph of an exponential...Ch. 3.1 - In Exercises 19-24, the graph of an exponential...Ch. 3.1 - In Exercises 19-24, the graph of an exponential...Ch. 3.1 - In Exercises 25-34, begin by graphing f(x)=2x ....Ch. 3.1 - In Exercises 25-34, begin by graphing . Then use...Ch. 3.1 - In Exercises 25-34, begin by graphing f(x)=2x ....Ch. 3.1 - In Exercises 25-34, begin by graphing f(x)=2x ....Ch. 3.1 - In Exercises 25-34, begin by graphing . Then use...Ch. 3.1 - In Exercises 25-34, begin by graphing . Then use...Ch. 3.1 - In Exercises 25-34, begin by graphing . Then use...Ch. 3.1 - In Exercises 25-34, begin by graphing . Then use...Ch. 3.1 - In Exercises 25-34, begin by graphing . Then use...Ch. 3.1 - In Exercises 25-34, begin by graphing . Then use...Ch. 3.1 - The figure shows the graph of f(x)=c4 . In...Ch. 3.1 - The figure shows the graph of . In Exercises...Ch. 3.1 - The figure shows the graph of f(x)=c4 . In...Ch. 3.1 - The figure shows the graph of . In Exercises...Ch. 3.1 - The figure shows the graph of f(x)=c4 . In...Ch. 3.1 - The figure shows the graph of f(x)=c4 . In...Ch. 3.1 - The figure shows the graph of . In Exercises...Ch. 3.1 - The figure shows the graph of . In Exercises...Ch. 3.1 - The figure shows the graph of . In Exercises...Ch. 3.1 - The figure shows the graph of . In Exercises...Ch. 3.1 - The figure shows the graph of f(x)=c4 . In...Ch. 3.1 - The figure shows the graph of f(x)=c4 . In...Ch. 3.1 - In Exercises 47-52, graph functions f anti g in...Ch. 3.1 - In Exercises 47-52, graph functions f and g in the...Ch. 3.1 - In Exercises 47-52, graph functions f and g in the...Ch. 3.1 - In Exercises 47-52, graph functions f and g in the...Ch. 3.1 - In Exercises 47-52, graph functions f and g in the...Ch. 3.1 - In Exercises 47-52, graph functions f and g in the...Ch. 3.1 - Use the compound interest formulas A=P(1+rn)nt and...Ch. 3.1 - Use the compound interest formulas A=P(1+rn)nt and...Ch. 3.1 - Use the compound interest formulas and to solve...Ch. 3.1 - Use the compound interest formulas and to solve...Ch. 3.1 - In Exercises 57-58, graph f and g in the same...Ch. 3.1 - In Exercises 57-58, graph f arid g in the same...Ch. 3.1 - Graph y=2r and x=2y in the same rectangular...Ch. 3.1 - 60. Graph and in the same rectangular coordinate...Ch. 3.1 - In Exercises 61-64, give the equation of each...Ch. 3.1 - In Exercises 61-64, give the equation of each...Ch. 3.1 - In Exercises 61-64, give the equation of each...Ch. 3.1 - In Exercises 61-64, give the equation of each...Ch. 3.1 - Use a calculator with a key or a key to solve...Ch. 3.1 - Use a calculator with a yx key or a key to solve...Ch. 3.1 - Use a calculator with a yx key or a key to solve...Ch. 3.1 - Use a calculator with a key or a key to solve...Ch. 3.1 - Use a calculator with a yx key or a key to solve...Ch. 3.1 - Use a calculator with a yx key or a key to solve...Ch. 3.1 - Use a calculator with an key to solve Exercises...Ch. 3.1 - Use a calculator with an key to solve Exercises...Ch. 3.1 - Use a calculator with on key to solve Exercises...Ch. 3.1 - Use a calculator with an ex key to solve Exercises...Ch. 3.1 - The functions model the percentage of college...Ch. 3.1 - The functions f(x)=643(1027)randg(x)=4091+66e0049x...Ch. 3.1 - 77. What is an exponential function? Ch. 3.1 - What is the natural exponential function?Ch. 3.1 - 79. Use a calculator to evaluate for and...Ch. 3.1 - 80. Describe how you could use the graph of to...Ch. 3.1 - 81. You have $10,000 to invest. One bank pays 5%...Ch. 3.1 - 82. a. Graph and rectangle. b. Graph and in the...Ch. 3.1 - Make Sense? In Exercises 83-86, determine whether...Ch. 3.1 - Make Sense? In Exercises 83-86, determine whether...Ch. 3.1 - Make Sense? In Exercises 83-86, determine whether...Ch. 3.1 - Explaining the Concepts I use the natural base e...Ch. 3.1 - In Exercises 87-90, determine whether each...Ch. 3.1 - In Exercises 87-90, determine whether each...Ch. 3.1 - In Exercises 87-90, determine whether each...Ch. 3.1 - In Exercises 87-90, determine whether each...Ch. 3.1 - The graphs labeled (a)-(d) in the figure represent...Ch. 3.1 - Prob. 92PECh. 3.1 - Prob. 93PECh. 3.1 - Solve for y;7x+3y=18 (Section 1.3. Example 7)Ch. 3.1 - 95. Find all zeros of (Section 3.4, Example 4) Ch. 3.1 - 96. Solve and graph the solution set on a number...Ch. 3.1 - Prob. 97PECh. 3.1 - Prob. 98PECh. 3.1 - Prob. 99PECh. 3.2 - Check Point 1 Write each equation in its...Ch. 3.2 - Check Point 2 Write each equation in its...Ch. 3.2 - Check Point 3 Evaluate:...Ch. 3.2 - Check Point 4 Evaluate: b. . Ch. 3.2 - Check Point 5 Evaluate: b. Ch. 3.2 - Check Point 6 Graph f(x)=3xandg(x)log3x in the...Ch. 3.2 - Check Point 7 Find the domain of f(x)=log4(x5).Ch. 3.2 - Check Point 8 Use the function in Example 8 to...Ch. 3.2 - Check Point 9 Use the formula in Example 9 to...Ch. 3.2 - Check Point 10 Find the domain of each function:...Ch. 3.2 - Check Point 11 Use the function in Example 11 to...Ch. 3.2 - 1. is equivalent to the exponential...Ch. 3.2 - Prob. 2CVCCh. 3.2 - Prob. 3CVCCh. 3.2 - Prob. 4CVCCh. 3.2 - Prob. 5CVCCh. 3.2 - Prob. 6CVCCh. 3.2 - Prob. 7CVCCh. 3.2 - Prob. 8CVCCh. 3.2 - Prob. 9CVCCh. 3.2 - Prob. 10CVCCh. 3.2 - Prob. 11CVCCh. 3.2 - Prob. 12CVCCh. 3.2 - Fill in each blank so that the resulting statement...Ch. 3.2 - Prob. 14CVCCh. 3.2 - Fill in each blank so that the resulting statement...Ch. 3.2 - In Exercises 1-8, write each equation in its...Ch. 3.2 - In Exercises 1-8, write each equation in its...Ch. 3.2 - In Exercises 1-8, write each equation in its...Ch. 3.2 - In Exercises 1-8, write each equation in its...Ch. 3.2 - In Exercises 1-8, write each equation in its...Ch. 3.2 - In Exercises 1-8, write each equation in its...Ch. 3.2 - In Exercises 1-8, write each equation in its...Ch. 3.2 - In Exercises 1-8, write each equation in its...Ch. 3.2 - In Exercises 9-20, write each equation in its...Ch. 3.2 - In Exercises 9-20, write each equation in its...Ch. 3.2 - In Exercises 9-20, write each equation in its...Ch. 3.2 - In Exercises 9-20, write each equation in its...Ch. 3.2 - In Exercises 9-20, write each equation in its...Ch. 3.2 - In Exercises 9-20, write each equation in its...Ch. 3.2 - In Exercises 9-20, write each equation in its...Ch. 3.2 - In Exercises 9-20, write each equation in its...Ch. 3.2 - In Exercises 9-20, write each equation in its...Ch. 3.2 - In Exercises 9-20, write each equation in its...Ch. 3.2 - In Exercises 9-20, write each equation in its...Ch. 3.2 - In Exercises 9-20, write each equation in its...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - log218 In Exercises 21-42, evaluate each...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21-42, evaluate each expression...Ch. 3.2 - In Exercises 21- 42, evaluate each expression...Ch. 3.2 - In Exercises 21- 42, evaluate each expression...Ch. 3.2 - 43. Graph and in the same rectangular coordinate...Ch. 3.2 - 44. Graph and in the same rectangular coordinate...Ch. 3.2 - 45. Graph and in the same rectangular coordinate...Ch. 3.2 - 16. Graph and in the same rectangular coordinate...Ch. 3.2 - In Exercises 47-52, the graph of a logarithmic...Ch. 3.2 - In Exercises 47-52, the graph of a logarithmic...Ch. 3.2 - In Exercises 47-52, the graph of a logarithmic...Ch. 3.2 - In Exercises 47-52, the graph of a logarithmic...Ch. 3.2 - In Exercises 47-52, the graph of a logarithmic...Ch. 3.2 - In Exercises 47-52, the graph of a logarithmic...Ch. 3.2 - In Exercises 53-58, begin by graphing...Ch. 3.2 - In Exercises 53-58, begin by graphing f(x)=log2x ....Ch. 3.2 - In Exercises 53-58, begin by graphing f(x)=log2x ....Ch. 3.2 - In Exercises 53-58, begin by graphing Then use...Ch. 3.2 - In Exercises 53-58, begin by graphing f(x)=log2x....Ch. 3.2 - In Exercises 53-58, begin by graphing f(x)=log2x ....Ch. 3.2 - The figure shows the graph of f(x)=logx. In...Ch. 3.2 - The figure shows the graph of . In Exercises...Ch. 3.2 - The figure shows the graph of f(x)=logx . In...Ch. 3.2 - The figure shows the graph of . In Exercises...Ch. 3.2 - The figure shows the graph of f(x)=logx . In...Ch. 3.2 - The figure shows the graph of f(x)=logx . In...Ch. 3.2 - The figure shows the graph of . In Exercises...Ch. 3.2 - The figure shows the graph of . In Exercises...Ch. 3.2 - The figure shows the graph of . In Exercises...Ch. 3.2 - The figure shows the graph of f(x)=lnx . In...Ch. 3.2 - The figure shows the graph of f(x)=lnx . In...Ch. 3.2 - The figure shows the graph of . In Exercises...Ch. 3.2 - The figure shows the graph of f(x)=lnx . In...Ch. 3.2 - The figure shows the graph of f(x)=lnx . In...Ch. 3.2 - The figure shows the graph of . In Exercises...Ch. 3.2 - The figure shows the graph of . In Exercises...Ch. 3.2 - In Exercises 75-80, find the domain of each...Ch. 3.2 - In Exercises 75-80, find the domain of each...Ch. 3.2 - In Exercises 75-80, find the domain of each...Ch. 3.2 - In Exercises 75-80, find the domain of each...Ch. 3.2 - In Exercises 75-80, find the domain of each...Ch. 3.2 - f(x)=ln(x7)2Ch. 3.2 - 81. log 100 Ch. 3.2 - In Exercises 81-100, evaluate or simplify each...Ch. 3.2 - In Exercises 81-100, evaluate or simplify each...Ch. 3.2 - 84. log 108 Ch. 3.2 - 85. 10 log 33 Ch. 3.2 - 86. 10 log 53 Ch. 3.2 - In 1Ch. 3.2 - 88. In e Ch. 3.2 - In e 6Ch. 3.2 - 90. In e7 Ch. 3.2 - ln1e6Ch. 3.2 - In Exercises 81-100, evaluate or simplify each...Ch. 3.2 - In Exercises 81-100, evaluate or simplify each...Ch. 3.2 - In Exercises 81-100, evaluate or simplify each...Ch. 3.2 - In Exercises 81-100, evaluate or simplify each...Ch. 3.2 - In Exercises 81-100, evaluate or simplify each...Ch. 3.2 - In Exercises 81-100, evaluate or simplify each...Ch. 3.2 - In Exercises 81-100, evaluate or simplify each...Ch. 3.2 - In Exercises 81-100, evaluate or simplify each...Ch. 3.2 - In Exercises 81-100, evaluate or simplify each...Ch. 3.2 - In Exercises 101-104, write each equation in its...Ch. 3.2 - In Exercises 101-104, write each equation in its...Ch. 3.2 - In Exercises 101-104, write each equation in its...Ch. 3.2 - In Exercises 101-104, write each equation in its...Ch. 3.2 - In Exercises 105-108, evaluate each expression...Ch. 3.2 - In Exercises 105-108, evaluate each expression...Ch. 3.2 - In Exercises 105-108, evaluate each expression...Ch. 3.2 - In Exercises 105-108, evaluate each expression...Ch. 3.2 - In Exercises 109-112, find the domain of each...Ch. 3.2 - In Exercises 109-112, find the domain of each...Ch. 3.2 - In Exercises 109-112, find the domain of each...Ch. 3.2 - In Exercises 109-112, find the domain of each...Ch. 3.2 - The percentage of adult height attained by a girl...Ch. 3.2 - The percentage of adult height attained by a girl...Ch. 3.2 - 115. The function models the wives' weekly...Ch. 3.2 - The bar graph shows the average number of hours...Ch. 3.2 - The loudness level of a sound, D, in decibels, is...Ch. 3.2 - The loudness level of a sound, D. in decibels, is...Ch. 3.2 - Students in a psychology class look a Pinal...Ch. 3.2 - 120. Describe the relationship between an equation...Ch. 3.2 - 121. What question can be asked to help evaluate...Ch. 3.2 - 122. Explain why the logarithm of 1 with base b is...Ch. 3.2 - Describe the following property using words:...Ch. 3.2 - Explain how to use the graph of f(x)=2x to obtain...Ch. 3.2 - Explain how to find the domain of a logarithmic...Ch. 3.2 - Logarithmic models are well soiled to phenomena in...Ch. 3.2 - 127. Suppose that a girl is 4 feet 6 inches at age...Ch. 3.2 - In Exercises 128-131, graph f mill g in the some...Ch. 3.2 - In Exercises 128-131, graph f and g in the same...Ch. 3.2 - In Exercises 128-131, graph f and g in the same...Ch. 3.2 - In Exercises 128-131, graph f and g in the same...Ch. 3.2 - 132. Students in a mathematics class look a final...Ch. 3.2 - 133. In parts (a)-(c).graph f and g in the same...Ch. 3.2 - Graph each of the following functions in the same...Ch. 3.2 - Make Sense? In Exercises 135-138, determine...Ch. 3.2 - Make Sense? In Exercises 135-138, determine...Ch. 3.2 - Make Sense? In Exercises 135-138, determine...Ch. 3.2 - Make Sense? In Exercises 135-138, determine...Ch. 3.2 - In Exercises 139-142, determine whether each...Ch. 3.2 - In Exercises 139-142, determine whether each...Ch. 3.2 - In Exercises 139-142, determine whether each...Ch. 3.2 - In Exercises 139-142, determine whether each...Ch. 3.2 - Without using a calculator, find the exact value...Ch. 3.2 - 144. Without using a calculator, find the exact...Ch. 3.2 - Without using a calculator, determine which is the...Ch. 3.2 - 146. This group exercise involves exploring the...Ch. 3.2 - 147. Three or the richest comedians in the United...Ch. 3.2 - 148. If , find (Section 2.2, Example 8) Ch. 3.2 - 149. Find the inverse of . (Section 2.7, Example...Ch. 3.2 - Exercises 150-152 will help you prepare for the...Ch. 3.2 - Exercises 150-152 will help you prepare for the...Ch. 3.2 - Exercises 150-152 will help you prepare for the...Ch. 3.3 - Check Point 1 Use the product rule to expand each...Ch. 3.3 - Prob. 2CPCh. 3.3 - Check Point 3 Use the power rule to expand each...Ch. 3.3 - Prob. 4CPCh. 3.3 - Prob. 5CPCh. 3.3 - Prob. 6CPCh. 3.3 - Prob. 7CPCh. 3.3 - Prob. 8CPCh. 3.3 - Prob. 1CVCCh. 3.3 - Prob. 2CVCCh. 3.3 - Prob. 3CVCCh. 3.3 - Prob. 4CVCCh. 3.3 - Prob. 1PECh. 3.3 - Prob. 2PECh. 3.3 - In Exercises 1-40, use properties of logarithms to...Ch. 3.3 - Prob. 4PECh. 3.3 - Prob. 5PECh. 3.3 - Prob. 6PECh. 3.3 - Prob. 7PECh. 3.3 - Prob. 8PECh. 3.3 - Prob. 9PECh. 3.3 - Prob. 10PECh. 3.3 - Prob. 11PECh. 3.3 - Prob. 12PECh. 3.3 - Prob. 13PECh. 3.3 - Prob. 14PECh. 3.3 - Prob. 15PECh. 3.3 - Prob. 16PECh. 3.3 - Prob. 17PECh. 3.3 - In Exercises 1-40, use properties of logarithms to...Ch. 3.3 - Prob. 19PECh. 3.3 - Prob. 20PECh. 3.3 - Prob. 21PECh. 3.3 - Prob. 22PECh. 3.3 - Prob. 23PECh. 3.3 - In Exercises 1-40, use properties of logarithms to...Ch. 3.3 - Prob. 25PECh. 3.3 - Prob. 26PECh. 3.3 - Prob. 27PECh. 3.3 - Prob. 28PECh. 3.3 - Prob. 29PECh. 3.3 - Prob. 30PECh. 3.3 - Prob. 31PECh. 3.3 - Prob. 32PECh. 3.3 - Prob. 33PECh. 3.3 - Prob. 34PECh. 3.3 - Prob. 35PECh. 3.3 - Prob. 36PECh. 3.3 - Prob. 37PECh. 3.3 - Prob. 38PECh. 3.3 - Prob. 39PECh. 3.3 - Prob. 40PECh. 3.3 - Prob. 41PECh. 3.3 - Prob. 42PECh. 3.3 - Prob. 43PECh. 3.3 - Prob. 44PECh. 3.3 - Prob. 45PECh. 3.3 - Prob. 46PECh. 3.3 - Prob. 47PECh. 3.3 - Prob. 48PECh. 3.3 - Prob. 49PECh. 3.3 - Prob. 50PECh. 3.3 - Prob. 51PECh. 3.3 - Prob. 52PECh. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises -41-70, use properties of logarithms...Ch. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises 1-40, use properties of logarithms to...Ch. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises 41-70, use properties of logarithms...Ch. 3.3 - In Exercises 71–78, use common logarithms or...Ch. 3.3 - In Exercises 71-78, use common logarithms or...Ch. 3.3 - In Exercises 71-78, use common logarithms or...Ch. 3.3 - In Exercises 71-78, use common logarithms or...Ch. 3.3 - In Exercises 71-78, use common logarithms or...Ch. 3.3 - In Exercises 71-78, use common logarithms or...Ch. 3.3 - In Exercises 71-78, use common logarithms or...Ch. 3.3 - In Exercises 71-78, use common logarithms or...Ch. 3.3 - In Exercises 79-82, use a graphing utility and the...Ch. 3.3 - In Exercises 79-82, use a graphing utility and the...Ch. 3.3 - In Exercises 79-82, use a graphing utility and the...Ch. 3.3 - In Exercises 79-82, use a graphing utility and the...Ch. 3.3 - In Exercises 83-88, let and . Write each...Ch. 3.3 - In Exercises 83-88, let logb2=A and logb3=C ....Ch. 3.3 - In Exercises 83-88, let and . Write each...Ch. 3.3 - In Exercises 83-SS. let logb2=A and logb3=C ....Ch. 3.3 - In Exercises 83-88, let logb2=A and logb3=C. Write...Ch. 3.3 - In Exercises 83-88, let and . Write each...Ch. 3.3 - In Exercises 89-102, determine whether each...Ch. 3.3 - In Exercises 89-102, determine whether each...Ch. 3.3 - In Exercises 89-102, determine whether each...Ch. 3.3 - In Exercises 89-102, determine whether each...Ch. 3.3 - In Exercises 89-102, determine whether each...Ch. 3.3 - In Exercises 89-102, determine whether each...Ch. 3.3 - In Exercises 89-102, determine whether each...Ch. 3.3 - In Exercises 89-102, determine whether each...Ch. 3.3 - In Exercises 89-102, determine whether each...Ch. 3.3 - In Exercises 89-102, determine whether each...Ch. 3.3 - In Exercises 89-102, determine whether each...Ch. 3.3 - In Exercises 89-102, determine whether each...Ch. 3.3 - In Exercises 89–102, determine whether each...Ch. 3.3 - In Exercises 89-102, determine whether each...Ch. 3.3 - 103. The loudness level of a sound can be...Ch. 3.3 - 104 The formula describes the time. t in weeks,...Ch. 3.3 - 105. Describe the product rule for logarithms and...Ch. 3.3 - Describe the quotient rule for logarithms and give...Ch. 3.3 - Describe the power rule for logarithms and give an...Ch. 3.3 - 108. Without showing l he details, explain how to...Ch. 3.3 - Describe the change-of-base properly and give an...Ch. 3.3 - Explain how to use your calculator to find log14...Ch. 3.3 - 111. You overhear a student talking about a...Ch. 3.3 - Find In 2 using a calculator. Then calculate each...Ch. 3.3 - a. Use a graphing utility (and the change-of-base...Ch. 3.3 - Graph y=logx, y=log(10x), and y=log(0.1x) in the...Ch. 3.3 - 115. Use a graphing utility and the change-of-base...Ch. 3.3 - Disprove each statement in Exercises 116-120...Ch. 3.3 - Disprove each statement in Exercises 116-120 by a...Ch. 3.3 - Disprove each statement in Exercises 116-120 by a....Ch. 3.3 - Disprove each statement in Exercises 116-120 by a...Ch. 3.3 - Disprove each statement in Exercises 116-120 by a....Ch. 3.3 - Make Sense? In Exercises 121-124. determine...Ch. 3.3 - Make Sense? In Exercises 121-124, determine...Ch. 3.3 - Make Sense? In Exercises 121-124, determine...Ch. 3.3 - Make Sense? In Exercises 121-124, determine...Ch. 3.3 - In Exercises 125-128, determine whether each...Ch. 3.3 - In Exercises 125-128, determine whether each...Ch. 3.3 - In Exercises 125-128, determine whether each...Ch. 3.3 - In Exercises 125-128, determine whether each...Ch. 3.3 - 129. Use the change-of-base property to prove...Ch. 3.3 - If log3=A and log7=B, find log79 in terms of A and...Ch. 3.3 - Write as a single term that does not contain a...Ch. 3.3 - 132. If f(x) - logb x, show that Ch. 3.3 - 133. Use the proof of the product rule in the...Ch. 3.3 - 134. Given , find each of the following: a. b. the...Ch. 3.3 - 135. Use the Leading Coefficient Test to determine...Ch. 3.3 - 136. Graph: (Section 3.5, Example 6) Ch. 3.3 - Exercises 137-139 will help you prepare for the...Ch. 3.3 - Exercises 137-139 will help you prepare for the...Ch. 3.3 - Exercises 137-139 will help you prepare for the...Ch. 3.3 - In Exercises 1-5, graph f and g in the same...Ch. 3.3 - In Exercises 1-5, graph f and g in the same...Ch. 3.3 - In Exercises 1-5, graph f and g in the same...Ch. 3.3 - In Exercises 1-5, graph f and g in the same...Ch. 3.3 - In Exercises 1-5, graph f and g in the same...Ch. 3.3 - In Exercises 6-9, find the domain of each...Ch. 3.3 - Prob. 7MCCPCh. 3.3 - Prob. 8MCCPCh. 3.3 - Prob. 9MCCPCh. 3.3 - Prob. 10MCCPCh. 3.3 - Prob. 11MCCPCh. 3.3 - Prob. 12MCCPCh. 3.3 - Prob. 13MCCPCh. 3.3 - Prob. 14MCCPCh. 3.3 - Prob. 15MCCPCh. 3.3 - Prob. 16MCCPCh. 3.3 - Prob. 17MCCPCh. 3.3 - Prob. 18MCCPCh. 3.3 - Prob. 19MCCPCh. 3.3 - In Exercises 10-20, evaluate each expression...Ch. 3.3 - Prob. 21MCCPCh. 3.3 - Prob. 22MCCPCh. 3.3 - Prob. 23MCCPCh. 3.3 - Prob. 24MCCPCh. 3.3 - Prob. 25MCCPCh. 3.3 - Prob. 26MCCPCh. 3.4 - Check Point 1 Solve: ...Ch. 3.4 - Check Point 2 Solve: b. . Ch. 3.4 - Check Point 3 Solve: 7e2x5=58. Find the solution...Ch. 3.4 - Prob. 4CPCh. 3.4 - Prob. 5CPCh. 3.4 - Prob. 6CPCh. 3.4 - Prob. 7CPCh. 3.4 - Prob. 8CPCh. 3.4 - Check Point 9 Use the formula in Example 9 to...Ch. 3.4 - Prob. 10CPCh. 3.4 - Prob. 11CPCh. 3.4 - Prob. 1CVCCh. 3.4 - Prob. 2CVCCh. 3.4 - Prob. 3CVCCh. 3.4 - Prob. 4CVCCh. 3.4 - Prob. 5CVCCh. 3.4 - Prob. 6CVCCh. 3.4 - Prob. 7CVCCh. 3.4 - Prob. 8CVCCh. 3.4 - Prob. 9CVCCh. 3.4 - Prob. 10CVCCh. 3.4 - Prob. 11CVCCh. 3.4 - Solve each exponential equation in Exercises 1-22...Ch. 3.4 - Solve each exponential equation in Exercises 1-22...Ch. 3.4 - Solve each exponential equation in Exercises 1-22...Ch. 3.4 - Prob. 4PECh. 3.4 - Solve each exponential equation in Exercises 1-22...Ch. 3.4 - Prob. 6PECh. 3.4 - Solve each exponential equation in Exercises 1-22...Ch. 3.4 - Solve each exponential equation in Exercises 1-22...Ch. 3.4 - Solve each exponential equation in Exercises 1-22...Ch. 3.4 - Solve each exponential equation in Exercises 1-22...Ch. 3.4 - Solve each exponential equation in Exercises 1-22...Ch. 3.4 - Solve each exponential equation in Exercises 1-22...Ch. 3.4 - Prob. 13PECh. 3.4 - Solve each exponential equation in Exercises 1-22...Ch. 3.4 - Solve each exponential equation in Exercises 1-22...Ch. 3.4 - Prob. 16PECh. 3.4 - Prob. 17PECh. 3.4 - Prob. 18PECh. 3.4 - Solve each exponential equation in Exercises 1-22...Ch. 3.4 - Prob. 20PECh. 3.4 - Prob. 21PECh. 3.4 - Prob. 22PECh. 3.4 - Solve each exponential equation in Exercises 2318....Ch. 3.4 - Solve each exponential equation in Exercises...Ch. 3.4 - Solve each exponential apiarian in Exercises 2348....Ch. 3.4 - Solve each exponential equation in Exercises 2348....Ch. 3.4 - Strive each exponential equation in Exercises...Ch. 3.4 - Solve each exponential equation in Exercises...Ch. 3.4 - Solve each exponential equation in Exercises...Ch. 3.4 - Solve each exponential equation in Exercises 2348....Ch. 3.4 - Solve each exponential equation in Exercises...Ch. 3.4 - Solve each exponential equation in Exercises 2348....Ch. 3.4 - Solve each exponential equation in Exercises 2348....Ch. 3.4 - Solve each exponential equation in Exercises 2348....Ch. 3.4 - Solve each exponential equation in Exercises 2348....Ch. 3.4 - Solve each exponential equation in Exercises 2318....Ch. 3.4 - Solve each exponential equation in Exercises 2348....Ch. 3.4 - Solve each exponential equation in Exercises...Ch. 3.4 - Solve each exponential equation in Exercises 2348....Ch. 3.4 - Solve each exponential equation in Exercises...Ch. 3.4 - Solve each exponential equation in Exercises 2348....Ch. 3.4 - Solve each exponential equation in Exercises 2348....Ch. 3.4 - Solve each exponential equation in Exercises...Ch. 3.4 - Solve each exponential equation in Exercises 2348....Ch. 3.4 - Solve each exponential equation in Exercises...Ch. 3.4 - Solve each exponential equation in Exercises...Ch. 3.4 - Solve each exponential equation in Exercises 2348....Ch. 3.4 - Solve each exponential equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - Solve each logarithmic equation in Exercises...Ch. 3.4 - In Exercises 93-102, solve each equation....Ch. 3.4 - In Exercises 93-102, solve each equation. 94. Ch. 3.4 - In Exercises 93-102, solve each equation. 95. Ch. 3.4 - In Exercises 93-102, solve each equation. 96. Ch. 3.4 - In Exercises 93-102, solve each equation. 97....Ch. 3.4 - In Exercises 93-102, solve each equation. 98....Ch. 3.4 - In Exercises 93-102, solve each equation....Ch. 3.4 - In Exercises 93-102, solve each equation. 100. Ch. 3.4 - In Exercises 93-102, solve each equation....Ch. 3.4 - In Exercises 93-102, solve each equation. 102. Ch. 3.4 - 103. The formula models the population of...Ch. 3.4 - The formula A=25.1e0.0187t models the population...Ch. 3.4 - The function models the percentage of surface...Ch. 3.4 - The function f(x)=20(0.975)x models the percentage...Ch. 3.4 - In Exercises 107-110, complete the table for a...Ch. 3.4 - In Exercise 107-110, complete the table for a...Ch. 3.4 - In Excreted 107-110, complete the table for a...Ch. 3.4 - In Exercises 107-110, complete the table for a...Ch. 3.4 - In Exercises 111-114, complete the table for a...Ch. 3.4 - In Exercises 111-114, complete the table for a...Ch. 3.4 - In Exercises 111 114, complete the table for a...Ch. 3.4 - In Exercises 111-114, complete the table for a...Ch. 3.4 - By 2019, nearly $1 out of every $5 spent in the...Ch. 3.4 - By 2019, nearly S1 out of every S5 spent in the...Ch. 3.4 - The function P(x)=9530log2x models the percentage,...Ch. 3.4 - The function models the percentage, P(x), of...Ch. 3.4 - The pH scale is used to measure the acidity or...Ch. 3.4 - The pH scale is used to measure the acidity or...Ch. 3.4 - Prob. 121PECh. 3.4 - Prob. 122PECh. 3.4 - Prob. 123PECh. 3.4 - Prob. 124PECh. 3.4 - Prob. 125PECh. 3.4 - Prob. 126PECh. 3.4 - Prob. 127PECh. 3.4 - Prob. 128PECh. 3.4 - Prob. 129PECh. 3.4 - Prob. 130PECh. 3.4 - Prob. 131PECh. 3.4 - Prob. 132PECh. 3.4 - Prob. 133PECh. 3.4 - Prob. 134PECh. 3.4 - Prob. 135PECh. 3.4 - Prob. 136PECh. 3.4 - Prob. 137PECh. 3.4 - Prob. 138PECh. 3.4 - Prob. 139PECh. 3.4 - Prob. 140PECh. 3.4 - Prob. 141PECh. 3.4 - Prob. 142PECh. 3.4 - Prob. 143PECh. 3.4 - Prob. 144PECh. 3.4 - Prob. 145PECh. 3.4 - Prob. 146PECh. 3.4 - Prob. 147PECh. 3.4 - Prob. 148PECh. 3.4 - 149. Research applications of logarithmic...Ch. 3.4 - Prob. 150PECh. 3.4 - Prob. 151PECh. 3.4 - Solve the equation x39x2+26x24=0 given that 4 is a...Ch. 3.4 - Prob. 153PECh. 3.4 - Exercises 153-155 will help you prepare for the...Ch. 3.4 - Exercises 153-155 will help you prepare for the...Ch. 3.5 - Check Point 1 In 2000, the population of Africa...Ch. 3.5 - Prob. 2CPCh. 3.5 - Check Point 3 In a learning theory project,...Ch. 3.5 - Prob. 4CPCh. 3.5 - Check Point 5 Table 3.7 shows the populations of...Ch. 3.5 - Prob. 6CPCh. 3.5 - Check Point 7 Use the models f(x)=0.074x+2.294 and...Ch. 3.5 - Prob. 8CPCh. 3.5 - Fill in each blank so that the resulting statement...Ch. 3.5 - Prob. 2CVCCh. 3.5 - Prob. 3CVCCh. 3.5 - Prob. 4CVCCh. 3.5 - Prob. 5CVCCh. 3.5 - Prob. 6CVCCh. 3.5 - Prob. 7CVCCh. 3.5 - The exponential models describe the population of...Ch. 3.5 - The exponential models describe the population of...Ch. 3.5 - Prob. 3PECh. 3.5 - The exponential models describe the population of...Ch. 3.5 - The exponential models describe the population of...Ch. 3.5 - Prob. 6PECh. 3.5 - About the size of New Jersey, Israel has seen its...Ch. 3.5 - About the size of New Jersey, Israel has seen its...Ch. 3.5 - In Exercises 9-14, complete the table. Round...Ch. 3.5 - In Exercises 9-14, complete the table. Round...Ch. 3.5 - Prob. 11PECh. 3.5 - Prob. 12PECh. 3.5 - In Exercises 9-14, complete the table. Round...Ch. 3.5 - Prob. 14PECh. 3.5 - Prob. 15PECh. 3.5 - Prob. 16PECh. 3.5 - Prob. 17PECh. 3.5 - Prob. 18PECh. 3.5 - Use the exponential decay model for carbon-14,...Ch. 3.5 - Use the exponential decay model for carbon-14, ,...Ch. 3.5 - Prob. 21PECh. 3.5 - Prob. 22PECh. 3.5 - Prob. 23PECh. 3.5 - Prob. 24PECh. 3.5 - Prob. 25PECh. 3.5 - Prob. 26PECh. 3.5 - Prob. 27PECh. 3.5 - Use the exponential decay model, A=A0ekt , to...Ch. 3.5 - Prob. 29PECh. 3.5 - Prob. 30PECh. 3.5 - Prob. 31PECh. 3.5 - Prob. 32PECh. 3.5 - Prob. 33PECh. 3.5 - Prob. 34PECh. 3.5 - Prob. 35PECh. 3.5 - Prob. 36PECh. 3.5 - 37. The logistic growth function describes the...Ch. 3.5 - Prob. 38PECh. 3.5 - Prob. 39PECh. 3.5 - Shown, again, in the following table is world...Ch. 3.5 - Shown, again, in the following table is world...Ch. 3.5 - Shown, again, in the following table is world...Ch. 3.5 - The logistic growth function models the...Ch. 3.5 - The logistic growth function models the...Ch. 3.5 - The logistic growth function P(x)=901+271e0.122x...Ch. 3.5 - The logistic growth Junction models the...Ch. 3.5 - Use Newtons Law of Cooling, T=C+(T0C)ekt, to solve...Ch. 3.5 - Use Newtons Law of Cooling, T=C+(T0C)ekt, to solve...Ch. 3.5 - Use Newton’s Law of Cooling, , to solve exercise...Ch. 3.5 - The Newtons Law of Cooling, T=C+(T0C)ekt, to solve...Ch. 3.5 - Exercises 47-52 present data in the form of...Ch. 3.5 - Exercises 47-51 present data in the form of...Ch. 3.5 - Exercises -17-52 present data in the form of...Ch. 3.5 - Exercises 47-52 present data in the form of...Ch. 3.5 - Exercises 47-52 present data in the form of...Ch. 3.5 - Exercises 47-52 present data in the form of...Ch. 3.5 - In Exercises 53-56, rewrite the equation in terms...Ch. 3.5 - In Exercises 53-56, rewrite the equation in terms...Ch. 3.5 - In Exercises 53-56, rewrite the equation in terms...Ch. 3.5 - In Exercises 53-56, rewrite the equation in terms...Ch. 3.5 - 57. Nigeria has a growth rate of 0.025 or 2.5%....Ch. 3.5 - How can you tell whether an exponential model...Ch. 3.5 - Suppose that a population that is growing...Ch. 3.5 - 60. What is the half-life of a substance? Ch. 3.5 - 61. Describe a difference between exponential...Ch. 3.5 - Describe the shape of a scatter plot that suggests...Ch. 3.5 - 63. You take up weightlifting and record the...Ch. 3.5 - Would you prefer that your salary be modeled...Ch. 3.5 - 65. One problem with all exponential growth models...Ch. 3.5 - In Example 1 on page 520, we used two data paints...Ch. 3.5 - In Example 1 on page 520, we used two data points...Ch. 3.5 - In Example 1 on page 520, we used two data points...Ch. 3.5 - In Example 1 on page 520, we used two data points...Ch. 3.5 - In Example 1 on page 520, we used two data points...Ch. 3.5 - The figure shows the number of people in the...Ch. 3.5 - In Exercises 47-52, you determined the best choice...Ch. 3.5 - Make Sense? In Exercises 73-76, determine whether...Ch. 3.5 - Make Sense? In Exercises 73-76, determine whether...Ch. 3.5 - Make Sense? In Exercises 73-76, determine whether...Ch. 3.5 - Make Sense? In Exercises 73-76, determine whether...Ch. 3.5 - The exponential growth models describe the...Ch. 3.5 - The exponential growth models describe the...Ch. 3.5 - The exponential growth models describe the...Ch. 3.5 - The exponential growth models describe the...Ch. 3.5 - Use Newtons Law of Cooling, T=C+(T0C)ekt, to solve...Ch. 3.5 - 82. Each group member should consult an almanac,...Ch. 3.5 - 83. After a 60% price reduction, you purchase a...Ch. 3.5 - Begin by graphing y=|x|. Then use this graph to...Ch. 3.5 - 85. Write an equation in point-slope form and...Ch. 3.5 - Exercises 86-88 will help you prepare for the...Ch. 3.5 - Exercises 86-88 will help you prepare for the...Ch. 3.5 - Exercises 86-88 will help you prepare for the...Ch. 3 - Prob. 1RECh. 3 - In Exercises 1-4, the graph of an exponential...Ch. 3 - In Exercises 1-4, the graph of an exponential...Ch. 3 - In Exercises 1-4, the graph of an exponential...Ch. 3 - In Exercises 5-9, graph f and g in the same...Ch. 3 - In Exercises 5-9, graph f and g in the same...Ch. 3 - In Exercises 59, graph f and g in the same...Ch. 3 - In Exercises 5-9, graph f and g in the same...Ch. 3 - In Exercises 5-9, graph f and g in the same...Ch. 3 - Use the compound interest formulas to solve...Ch. 3 - Suppose that you have $14,000 to invest. Which...Ch. 3 - A cup of coffee is taken out of a microwave oven...Ch. 3 - 13. Ch. 3 - 3=log4xCh. 3 - 15. Ch. 3 - In Exercises 16-18, write each equation in its...Ch. 3 - In Exercises 16-18, write each equation in its...Ch. 3 - In Exercises 16-18, write each equation in its...Ch. 3 - In Exercises 19-29, evaluate each expression...Ch. 3 - In Exercises 19-29, evaluate each expression...Ch. 3 - In Exercises 19-29, evaluate each expression...Ch. 3 - In Exercises 19-29, evaluate each expression...Ch. 3 - In Exercises 19-29, evaluate each expression...Ch. 3 - In Exercises 19-29, evaluate each expression...Ch. 3 - In Exercises 19-29, evaluate each expression...Ch. 3 - In Exercises 19-29, evaluate each expression...Ch. 3 - In Exercises 19-29, evaluate each expression...Ch. 3 - In Exercises 19-29, evaluate each expression...Ch. 3 - In Exercises 19-29, evaluate each expression...Ch. 3 - Graph f(x)=2x and g(x)=log2x in the same...Ch. 3 - Graph f(x)=(13)x and g(x)=log11x in the same...Ch. 3 - In Exercises 32-35, the graph of a logarithmic...Ch. 3 - In Exercises 32-35, the graph of a logarithmic...Ch. 3 - In Exercises 32-35, the graph of a logarithmic...Ch. 3 - In Exercises 32-35, the graph of a logarithmic...Ch. 3 - In Exercises 36-38, begin by graphing f(x)=log2x....Ch. 3 - In Exercises 36-38, begin by graphing Then use...Ch. 3 - In Exercises 36-38, begin by graphing Then use...Ch. 3 - In Exercises 39—40, graph f and g in the same...Ch. 3 - In Exercises 39-40, graph f and g in the same...Ch. 3 - In Exercises 41-43, find the domain of each...Ch. 3 - In Exercises 41-43, find the domain of each...Ch. 3 - In Exercises 41-43, find the domain of each...Ch. 3 - In Exercises 44-46, use inverse properties of...Ch. 3 - In Exercises 44-46, use inverse properties of...Ch. 3 - In Exercises 44-46, use inverse properties of...Ch. 3 - 47. On the Richter scale, the magnitude, R, of an...Ch. 3 - Students in a psychology class look a final...Ch. 3 - The formula t=1cln(AAN) describes the lime, t, in...Ch. 3 - In Exercises 50-53, use properties of logarithms...Ch. 3 - In Exercises 50-53, use properties of logarithms...Ch. 3 - In Exercises 50-53, use properties of logarithms...Ch. 3 - Prob. 53RECh. 3 - Prob. 54RECh. 3 - Prob. 55RECh. 3 - Prob. 56RECh. 3 - Prob. 57RECh. 3 - Prob. 58RECh. 3 - In Exercises 58-59, use common logarithms or...Ch. 3 - Prob. 60RECh. 3 - Prob. 61RECh. 3 - Prob. 62RECh. 3 - Prob. 63RECh. 3 - Prob. 64RECh. 3 - Prob. 65RECh. 3 - Prob. 66RECh. 3 - Prob. 67RECh. 3 - Prob. 68RECh. 3 - Prob. 69RECh. 3 - Prob. 70RECh. 3 - Prob. 71RECh. 3 - Prob. 72RECh. 3 - Prob. 73RECh. 3 - Prob. 74RECh. 3 - Prob. 75RECh. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - Prob. 78RECh. 3 - Prob. 79RECh. 3 - 80. The function models the average atmospheric...Ch. 3 - Prob. 81RECh. 3 - Prob. 82RECh. 3 - Prob. 83RECh. 3 - Prob. 84RECh. 3 - Prob. 85RECh. 3 - Prob. 86RECh. 3 - 87. Use the exponential decay model, , to solve...Ch. 3 - 88. The function. models the number of people...Ch. 3 - Prob. 89RECh. 3 - Prob. 90RECh. 3 - Prob. 91RECh. 3 - Prob. 92RECh. 3 - Prob. 93RECh. 3 - Prob. 94RECh. 3 - Prob. 95RECh. 3 - 1. Graph and in the same rectangular coordinate...Ch. 3 - Prob. 2TCh. 3 - Prob. 3TCh. 3 - Prob. 4TCh. 3 - Prob. 5TCh. 3 - Prob. 6TCh. 3 - Prob. 7TCh. 3 - Prob. 8TCh. 3 - Prob. 9TCh. 3 - Prob. 10TCh. 3 - Prob. 11TCh. 3 - Prob. 12TCh. 3 - Prob. 13TCh. 3 - Prob. 14TCh. 3 - Prob. 15TCh. 3 - Prob. 16TCh. 3 - Prob. 17TCh. 3 - Prob. 18TCh. 3 - Prob. 19TCh. 3 - Prob. 20TCh. 3 - Prob. 21TCh. 3 - Prob. 22TCh. 3 - Use the compound interest formulas to solve...Ch. 3 - Prob. 24TCh. 3 - Prob. 25TCh. 3 - Prob. 26TCh. 3 - Prob. 27TCh. 3 - Prob. 28TCh. 3 - Prob. 29TCh. 3 - Prob. 30TCh. 3 - Prob. 31TCh. 3 - In Exercises 30-33, determine whether the values...Ch. 3 - Prob. 33TCh. 3 - Prob. 34TCh. 3 - Prob. 1CRECh. 3 - Prob. 2CRECh. 3 - Prob. 3CRECh. 3 - Prob. 4CRECh. 3 - Prob. 5CRECh. 3 - Prob. 6CRECh. 3 - Prob. 7CRECh. 3 - Prob. 8CRECh. 3 - Prob. 9CRECh. 3 - Prob. 10CRECh. 3 - Prob. 11CRECh. 3 - Prob. 12CRECh. 3 - Prob. 13CRECh. 3 - Prob. 14CRECh. 3 - Prob. 15CRECh. 3 - Prob. 16CRECh. 3 - Prob. 17CRECh. 3 - Prob. 18CRECh. 3 - Prob. 19CRECh. 3 - Prob. 20CRE
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Text book image
College Algebra
Algebra
ISBN:9781938168383
Author:Jay Abramson
Publisher:OpenStax
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Text book image
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Chain Rule dy:dx = dy:du*du:dx; Author: Robert Cappetta;https://www.youtube.com/watch?v=IUYniALwbHs;License: Standard YouTube License, CC-BY
CHAIN RULE Part 1; Author: Btech Maths Hub;https://www.youtube.com/watch?v=TIAw6AJ_5Po;License: Standard YouTube License, CC-BY