
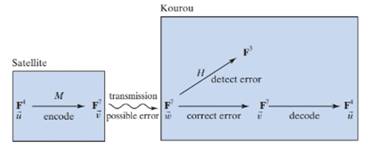
See Exercise 53 for some background. When information is transmitted, there may be some errors in the communication. We present a method of adding extra information to messages so that most errors that occur during transmission can be detected and corrected. Such methods are referred to as error-correcting codes. (Compare these with codes whose purpose is to conceal information.) The pictures of man’s first landing on the Moon (in 1969) were televised just as they had been received and were not very clear, since they contained many errors induced during transmission. On later missions, much clearer error-corrected pictures were obtained.
In computers, information is stored and processed in the form of strings of binary digits, 0 and 1. This stream of binary digits is often broken up into “blocks” of eight binary digits (bytes). For the sake of simplicity, we will work with blocks of only four binary digits (i.e., with
Suppose these vectors in
a. Let H he the Hamming matrix introduced in Exercise 53. How can the computer in Kourou use
b. Suppose the vector
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
Linear Algebra With Applications (classic Version)
- Use the graph to solve 3x2-3x-8=0arrow_forwardÎntr-un bloc sunt apartamente cu 2 camere și apartamente cu 3 camere , în total 20 de apartamente și 45 de camere.Calculați câte apartamente sunt cu 2 camere și câte apartamente sunt cu 3 camere.arrow_forward1.2.19. Let and s be natural numbers. Let G be the simple graph with vertex set Vo... V„−1 such that v; ↔ v; if and only if |ji| Є (r,s). Prove that S has exactly k components, where k is the greatest common divisor of {n, r,s}.arrow_forward
- Question 3 over a field K. In this question, MË(K) denotes the set of n × n matrices (a) Suppose that A Є Mn(K) is an invertible matrix. Is it always true that A is equivalent to A-¹? Justify your answer. (b) Let B be given by 8 B = 0 7 7 0 -7 7 Working over the field F2 with 2 elements, compute the rank of B as an element of M2(F2). (c) Let 1 C -1 1 [4] [6] and consider C as an element of M3(Q). Determine the minimal polynomial mc(x) and hence, or otherwise, show that C can not be diagonalised. [7] (d) Show that C in (c) considered as an element of M3(R) can be diagonalised. Write down all the eigenvalues. Show your working. [8]arrow_forwardR denotes the field of real numbers, Q denotes the field of rationals, and Fp denotes the field of p elements given by integers modulo p. You may refer to general results from lectures. Question 1 For each non-negative integer m, let R[x]m denote the vector space consisting of the polynomials in x with coefficients in R and of degree ≤ m. x²+2, V3 = 5. Prove that (V1, V2, V3) is a linearly independent (a) Let vi = x, V2 = list in R[x] 3. (b) Let V1, V2, V3 be as defined in (a). Find a vector v € R[×]3 such that (V1, V2, V3, V4) is a basis of R[x] 3. [8] [6] (c) Prove that the map ƒ from R[x] 2 to R[x]3 given by f(p(x)) = xp(x) — xp(0) is a linear map. [6] (d) Write down the matrix for the map ƒ defined in (c) with respect to the basis (2,2x + 1, x²) of R[x] 2 and the basis (1, x, x², x³) of R[x] 3. [5]arrow_forwardQuestion 4 (a) The following matrices represent linear maps on R² with respect to an orthonormal basis: = [1/√5 2/√5 [2/√5 -1/√5] " [1/√5 2/√5] A = B = [2/√5 1/√5] 1 C = D = = = [ 1/3/5 2/35] 1/√5 2/√5 -2/√5 1/√5' For each of the matrices A, B, C, D, state whether it represents a self-adjoint linear map, an orthogonal linear map, both, or neither. (b) For the quadratic form q(x, y, z) = y² + 2xy +2yz over R, write down a linear change of variables to u, v, w such that q in these terms is in canonical form for Sylvester's Law of Inertia. [6] [4]arrow_forward
- part b pleasearrow_forwardQuestion 5 (a) Let a, b, c, d, e, ƒ Є K where K is a field. Suppose that the determinant of the matrix a cl |df equals 3 and the determinant of determinant of the matrix a+3b cl d+3e f ГЪ e [ c ] equals 2. Compute the [5] (b) Calculate the adjugate Adj (A) of the 2 × 2 matrix [1 2 A = over R. (c) Working over the field F3 with 3 elements, use row and column operations to put the matrix [6] 0123] A = 3210 into canonical form for equivalence and write down the canonical form. What is the rank of A as a matrix over F3? 4arrow_forwardQuestion 2 In this question, V = Q4 and - U = {(x, y, z, w) EV | x+y2w+ z = 0}, W = {(x, y, z, w) € V | x − 2y + w − z = 0}, Z = {(x, y, z, w) € V | xyzw = 0}. (a) Determine which of U, W, Z are subspaces of V. Justify your answers. (b) Show that UW is a subspace of V and determine its dimension. (c) Is VU+W? Is V = UW? Justify your answers. [10] [7] '00'arrow_forward
- Tools Sign in Different masses and Indicated velocities Rotational inert > C C Chegg 39. The balls shown have different masses and speeds. Rank the following from greatest to least: 2.0 m/s 8.5 m/s 9.0 m/s 12.0 m/s 1.0 kg A 1.2 kg B 0.8 kg C 5.0 kg D C a. The momenta b. The impulses needed to stop the balls Solved 39. The balls shown have different masses and speeds. | Chegg.com Images may be subject to copyright. Learn More Share H Save Visit > quizlet.com%2FBoyE3qwOAUqXvw95Fgh5Rw.jpg&imgrefurl=https%3A%2F%2Fquizlet.com%2F529359992%2Fc. Xarrow_forwardSimplify the below expression. 3 - (-7)arrow_forward(6) ≤ a) Determine the following groups: Homz(Q, Z), Homz(Q, Q), Homz(Q/Z, Z) for n E N. Homz(Z/nZ, Q) b) Show for ME MR: HomR (R, M) = M.arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





