
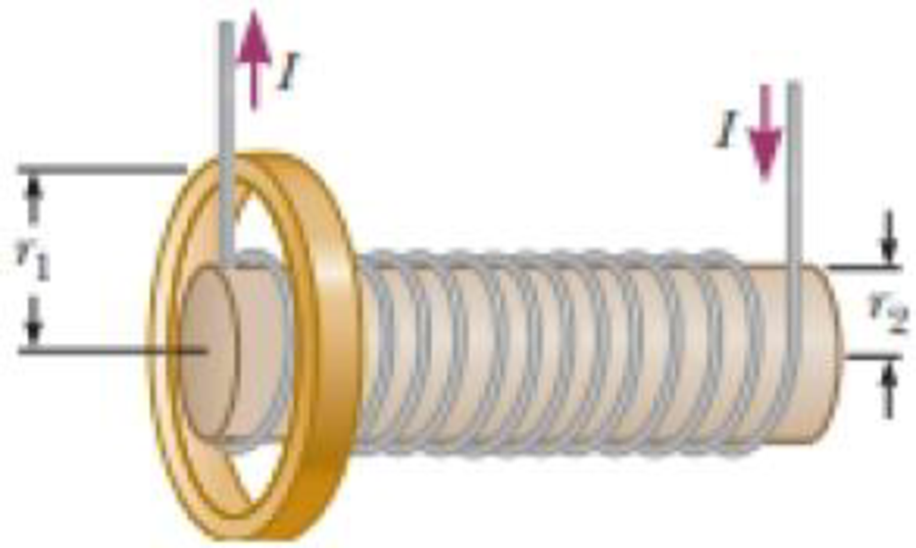
An aluminum ring of radius r1 = 5.00 cm and resistance 3.00 × 10−4 Ω is placed around one end of a long air-core solenoid with 1 000 turns per meter and radius r2 = 3.00 cm as shown in Figure P30.5. Assume the axial component of the field produced by the solenoid is one-half as strong over the area of the end of the solenoid as at the center of the solenoid. Also assume the solenoid produces negligible field outside its cross-sectional area. The current in the solenoid is increasing at a rate of 270 A/s. (a) What is the induced current in the ring? At the center of the ring, what are (b) the magnitude and (c) the direction of the magnetic field produced by the induced current in the ring?
Figure P30.5 Problems 5 and 6.
(a)
The induced current in the ring.
Answer to Problem 5P
The induced current in the ring is
Explanation of Solution
Given info: Radius of aluminum ring is
The magnetic field due to solenoid can be given as,
Here,
The area of the coil can be given as,
Here,
Substitute
The emf generated in the coil can be given as,
Here,
Substitute
Substitute
As the ring is placed around one end and also the field produced by the end of the solenoid is half at the centre of the solenoid.
Then, emf induced in the ring can be given as,
Here,
Substitute
The current induced in the ring can be given as,
Here,
Substitute
Thus, the current induced in the ring is
Conclusion:
Therefore, the current induced in the ring is
(b)
The magnitude of the magnetic field at the centre of the ring.
Answer to Problem 5P
The magnitude of the magnetic field at the centre of the ring is
Explanation of Solution
Given info: Radius of aluminum ring is
The magnetic field at the center of the ring can be given as,
Here,
Substitute
Thus, the magnitude of the magnetic field is
Conclusion:
Therefore, the magnitude of the magnetic field at the center of ring is
(c)
The direction of magnetic field at the center of the ring.
Answer to Problem 5P
The direction of magnetic field at the center of the ring is towards the left.
Explanation of Solution
Given info: Radius of aluminum ring is

Figure (1)
The solenoid’s field points to the right through the ring as shown in the figure (I). So, to oppose the increasing field, the direction of magnetic field at the center of the ring will be towards the left.
Conclusion:
Therefore, the direction of magnetic field at the center of the ring will be towards towards the left.
Want to see more full solutions like this?
Chapter 30 Solutions
Bundle: Physics For Scientists And Engineers With Modern Physics, Loose-leaf Version, 10th + Webassign Printed Access Card For Serway/jewett's Physics For Scientists And Engineers, 10th, Single-term
Additional Science Textbook Solutions
Essential University Physics (3rd Edition)
Loose Leaf For Explorations: Introduction To Astronomy
MODERN PHYSICS (LOOSELEAF)
College Physics: A Strategic Approach (4th Edition)
An Introduction to Thermal Physics
Physics (5th Edition)
- A solenoid has a ferromagnetic core, n = 1000 turns per meter, and I = 5.0 A. If B inside the solenoid is 2.0 T, what is for the core material?arrow_forwardA wire is bent in the form of a square loop with sides of length L (Fig. P30.24). If a steady current I flows in the loop, determine the magnitude of the magnetic field at point P in the center of the square. FIGURE P30.24arrow_forwardA long thin solenoid has 808 turns per meter and radius 3.00cm. The current in the solenoid is increasing at a rate of 60A/s. What is the magnitude of the induced electric field (in V/m) at a point near the center of the solenoid and 0.8cm from its axis?arrow_forward
- A long thin solenoid has 779 turns per meter and radius 2.00cm. The current in the solenoid is increasing at a rate 23 A/s. What is the magnitude of the induced Electric field (in V/m) at a point near the center of the solenoid and 1.3 cm from its axis?arrow_forwardAn aluminum ring of radius r1 = 5.00 cm and resistance 3.00 x 10-4 V is placed around one end of a long aircore solenoid with 1 000 turns per meter and radius r2 = 3.00 cm as shown. Assume the axial component of the field produced by the solenoid is one-half as strong over the area of the end of the solenoid as at the center of the solenoid. Also assume the solenoid produces negligible field outside its cross-sectional area. The current in the solenoid is increasing at a rate of 270 A/s. (a) What is the induced current in the ring? At the center of the ring, what are (b) the magnitude and (c) the direction of the magnetic field produced by the induced current in the ring?arrow_forwardAn aluminum ring of radius r₁=5.00 cm and a resistance of 3.95 x 10-4 is placed around one end of a long air-core solenoid with 900 turns per meter and radius r₂ = 3.00 cm as shown in the figure below. Assume the axial component of the field produced by the solenoid is one-half as strong over the area of the end of the solenoid as at the center of the solenoid. Also assume the solenoid produces negligible field outside its cross-sectional area. The current in the solenoid is increasing at a rate of 270 A/s. 71 0 (a) What is the induced current in the ring? A Ⓡ (b) At the center of the ring, what is the magnitude of the magnetic field produced by the induced current in the ring? μT (c) At the center of the ring, what is the direction of the magnetic field produced by the induced current in the ring? O to the left O to the right O upward O downwardarrow_forward
- The magnetic field at the center of a solenoid L = 65 cm long is B = 0.42 T when a current of I = 3.5 A flows through the solenoid wire. Part (a) Solve the formula for the magnetic field near the center of a long, tightly wound solenoid for the number of turns, N, in the solenoid. The expression should be in terms of the given variables. Part (b) Calculate the value of the number of turns, N.arrow_forward= 0.500 mm. The For a class demonstration, a professor needs to create a solenoid using copper wire with diameter d resistance of the solenoid needs to be 4.10 Q and the magnetic field of the solenoid with a current of 3.30 A should be 6.30 x 10-2 T. Assume the resistance does not change significantly with temperature, and the radius of the solenoid is 1.00 cm. (Use p = 1.70 x 10-8 0· m for the resistivity of copper.) (a) How many turns of wire does the professor need? turns (b) Determine the required length (in cm) of the solenoid. cmarrow_forwardA long solenoid (radius = 3.0 cm, 2500 turns per meter) carries a current given by I = 0.30 sin(200 t) A, where t is measured in s. When t = 2.5 ms, what is the magnitude of the induced electric field at a point which is 4.0 cm from the axis of the solenoid? O 9.3 x 10-3 V/m O 1.9 x 10-3 V/m O 8.0 x 10-3 V/m O 6.7 x 10-3 V/m O 5.3 10-3 V/marrow_forward
- An aluminum ring of radius r₁=5.00 cm and a resistance of 3.25 × 10-4 is placed around one end of a long air-core solenoid with 980 turns per meter and radius r₂ = 3.00 cm as shown in the figure below. Assume the axial component of the field produced by the solenoid is one-half as strong over the area of the end of the solenoid as at the center of the solenoid. Also assume the solenoid produces negligible field outside its cross-sectional area. The current in the solenoid is increasing at a rate of 270 A/s. r₁ 0 (a) What is the induced current in the ring? A (b) At the center of the ring, what is the magnitude of the magnetic field produced by the induced current in the ring? μTarrow_forwardThe magnetic field at the center of a solenoid L = 65 cm long is B = 0.13 T when a current of I = 6.5 A travels through the solenoid wire. Solve the formula for the magnetic field near the center of a long, tightly wound solenoid for the number of turns, N, in the solenoid. The expression should be in terms of the given variables.arrow_forwardSolenoid 1 is 50 cm long and has a cross-sectional diameter of 3.0 cm. This solenoid has a winding of 2000 turns per meter, and the electric current through the windings is changing at a rate dl/dt = 1.5 A/s. A small coil consisting of N = 20 turns has a cross- sectional diameter of 1.0 cm, and it is placed in the middle of the solenoid such that the plane of the coil is perpendicular to the central axis of the solenoid. Find the magnitude of the emf induced in this inside coil, solenoid 2. Solenoid 1 Solenoid 2 Common axisarrow_forward
 Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning




