
Concept explainers
Repeat Example 30.1, but use the midpoint method to generate your solution.
To calculate: The solution of the one-dimensional heat conduction equation using midpoint method for a thing rod of length
Answer to Problem 1P
Solution: The desired result is as shown below.
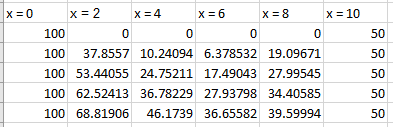
Explanation of Solution
Given Information:
The expression of the temperature distribution of long, thin rod is,
Calculation:
Calculate
and
The expression of temperature,
Rewrite the above equation,
Rewrite the above equation,
Substitute the value at t = 0.1 s for the node at x = 2 cm,
The results at the other interior points are,
Therefore,
Next,
And,
The value at t = 0.2 s; the interior points are four are,
Therefore,
Next,
And,
The Midpoint method in this subpart is,
And,
Use
predictor is calculating as follow:
Slop-midpoint,
Calculate corrector,
Use Excel to create the table as follow,
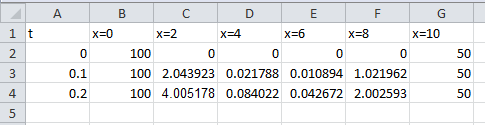
Use excel to solve this problem.
Step 1 Open the excel-spreadsheet and then press Alt+F11.
Step 2 Then there is a window opened in which write the coding to find optimal solution is as below,
Step 3 Now press F5, a new popup window will appear as shown below.
Step 4 Press run after selecting the program name, the desired result will be,
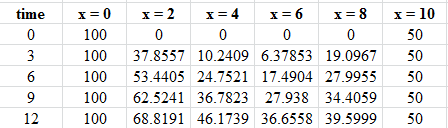
The flotation of the table is,
Want to see more full solutions like this?
Chapter 30 Solutions
Numerical Methods for Engineers
- Need detailed report without CHATGPT, accept if you can give with code and plots, previous reported Plots are required.arrow_forwardNeed detailed report without CHATGPT, accept if you can give with code and plots, previous reportedarrow_forward1. Which set of parametric equations is shown in the graph below? Explain your reasoning. a) x = t; y = t² b) x = = t²; y = t -3-2-1 5 4 3 2 1 12 3 2. Using the graph of f, a. determine whether dy/dt is positive or negative given that dx/dt is negative and b. determine whether dx/dt is positive or negative given that dy/dt is positive. Explain your reasoning. 2 f x 1 2 3 4arrow_forward
- Find the perimeter of the triangle. Express the perimeter using the same unit of measure that appears on the given sides. 9 ft 13 ft 6 ft The perimeter isarrow_forwardUse the formula for Pr to evaluate the following expression. 9P5 9P5 =☐arrow_forwardFind the volume of the figure. The volume of the figure is 3 m 3 m 3 marrow_forward
- Find the circumference and area of the circle. Express answers in terms of and then round to the nearest tenth. Find the circumference in terms of C= (Type an exact answer in terms of x.) Find the circumference rounded to the nearest tenth. C= Find the area in terms of A= (Type an exact answer in terms of x.) Find the area rounded to the nearest tenth. A= 10 cmarrow_forwardIn Exercises 62-64, sketch a reasonable graph that models the given situation. The number of hours of daylight per day in your hometown over a two-year period The motion of a diving board vibrating 10 inches in each direction per second just after someone has dived off The distance of a rotating beam of light from a point on a wallarrow_forwardThe manager of a fleet of automobiles is testing two brands of radial tires and assigns one tire of each brand at random to the two rear wheels of eight cars and runs the cars until the tires wear out. The data (in kilometers) follow. CAR BRAND1 BRAND2 DIFFERENCE = (BRAND1 - BF 1 36,925 33,018 3,907 2 45,300 43,280 2,020 3 36,240 35,500 740 4 32,100 31,200 900 5 37,210 37,015 195 6 48,360 46,800 1,560 7 38,200 37,810 390 8 33,500 33,215 285arrow_forward
- Diabetes and obesity are serious health concerns in the United States and much of the developed world. Measuring the amount of body fat a person carries is one way to monitor weight control progress, but measuring it accurately involves either expensive X-ray equipment or a pool in which to dunk the subject. Instead body mass index (BMI) is often used as a proxy for body fat because it is easy to measure: BMI = mass(kg)/(height(m))² = 703 mass(lb)/(height(in))². In a study of 15 men at TXST, both BMI and body fat were measured. Researchers imported the data into statistical software for analysis. A few values are missing from the output. Complete the table by filling in the missing values. Model Summary S R-sq % (three decimal places) (two decimal places. e.g. 12.3456%, enter 12.35) Analysis of Variance Source Model Error Total DF SS MS F P 17.600 0.001 DF: whole numbers SS or MS; three decimal places 34.810 Does a simple linear regression model seem reasonable in this situation?…arrow_forwardThe use of electromyostimulation (EMS) as a method to train healthy skeletal muscle is studied. EMS sessions consisted of 30 contractions (4-second duration, 85 Hz) and were carried out three times per week for three weeks on 17 ice hockey players. The 10-meter skating performance test showed a standard deviation of 0.90 seconds. Is there strong evidence to conclude that the standard deviation of performance time exceeds the historical value of 0.75 seconds? Use a = 0.05.arrow_forwardOne-Sample Z Test Test of М = 45 vs not === 45 The assumed standard deviation = 2.8 VARIABLE N MEAN STDEV SE MEAN X Instructions: 46.377 2.500 0.626 95% CI (,) Fill in the missing values. N: Round the answer to the nearest whole number. Cl: Round to three decimal places. Z: Round to two decimal places. P: Round to three decimal places.arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw HillAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw HillAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,





