
Concept explainers
(a)
The time taken by a ball released from an airplane to hit the ground.
Answer to Problem 69QAP
The ball hits the ground after 9.24 s.
Explanation of Solution
Given:
The speed of the airplane when the ball is released
Angle made by the plane to the horizontal
Height of the airplane above the ground when the ball is released
Formula used:
The time of flight of the ball is determined using the equation for the vertical motion of the ball.
Here,
Calculation:
When the airplane releases the ball, the ball has the velocity of the airplane. Its speed is 35.3 m/s and it is released at an angle 30.0o to the horizontal.
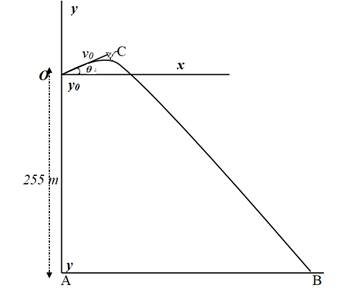
Assume the origin to be located at the point where the ball is released. With the x axis parallel to the ground and the + y axis directed upwards.
The ball travels a parabolic path and lands on the ground at point B. Its vertical displacement when it lands on the ground, is equal to
This is shown in the diagram below.
Calculate the vertical component of the ball's velocity.
The ball falls under the action of the gravitational force. Hence the acceleration acting on the ball in the vertical direction is the acceleration of free fall.
In equation (1), substitute
Solve the quadratic equation to determine t.
Taking the positive root,
Conclusion:
Thus, the ball hits the ground after 9.24 s.
(b)
The maximum height of the ball from the ground.
Answer to Problem 69QAP
The ball reaches a maximum height of 270.9 m from the ground.
Explanation of Solution
Given:
The speed of the airplane when the ball is released
Angle made by the plane to the horizontal
Height of the airplane above the ground when the ball is released
Formula used:
The maximum height reached by the ball can be calculated using the equation of motion,
Here, vy is vertical component of the ball's velocity at the position y,
The maximum height h reached by the ball, when measured from the ground is given by,
Calculation:
The vertical component of the ball's velocity reduces as it moves up, due to the action of the gravitational force. When the vertical component reaches a value zero, the ball can no longer make an upward displacement, hence after this point it starts its motion in the downward direction.
Therefore, at maximum height,
In equation (2) substitute 0 m/s for vy,
This point is 15.89 m above the point of projection. Therefore, its height from the ground is given by,
Conclusion:
Thus, the ball reaches a maximum height of 270.9 m from the ground.
(c)
The horizontal distance traveled by the ball from the point of release to the ground.
Answer to Problem 69QAP
The ball travels a horizontal distance of 282.5 m.
Explanation of Solution
Given:
The speed of the airplane when the ball is released
Angle made by the plane to the horizontal
Height of the airplane above the ground when the ball is released
Time of flight of the ball
Formula used:
The horizontal distance traveled by the ball is calculated using the equation
Here,
Calculation:
The ball makes a vertical displacement of
Calculate the horizontal component of the ball's velocity.
Substitute the values of v0x, ax and t in equation (3) and solve for
Conclusion:
Thus, the ball travels a horizontal distance of 282.5 m.
Want to see more full solutions like this?
Chapter 3 Solutions
FlipIt for College Physics (Algebra Version - Six Months Access)
- Diamond has an index of refraction of about 2.4. Suppose you cut a diamond so it has a flat surface, and shine a laser pointer beam so that it makes a 27 degree angle with respect to the normal line to that surface. What angle will the laser beam make with respect to the normal after it passes through the air-diamond boundary and is inside the diamond? Give your answer as the number of degrees.arrow_forwardFind current of each line of D,E, and F. Where V1 is 9V, V2 is 7V, R1 is 989 , R2 is 2160, R3 is 4630 , R4 is 5530, R5 is 6720, and E is 16V. Please explain all steps. Thank youarrow_forwardYou are tasked with designing a parallel-plate capacitor using two square metal plates, eachwith an area of 0.5 m², separated by a 0.1 mm thick layer of air. However, to increase the capacitance,you decide to insert a dielectric material with a dielectric constant κ = 3.0 between the plates. Describewhat happens (and why) to the E field between the plates when the dielectric is added in place of theair.arrow_forward
- Calculate the work required to assemble a uniform charge Q on a thin spherical shell of radiusR. Start with no charge and add infinitesimal charges dq until the total charge reaches Q, assuming thecharge is always evenly distributed over the shell’s surface. Show all steps.arrow_forwardRod AB is fixed to a smooth collar D, which slides freely along the vertical guide shown in (Figure 1). Point C is located just to the left of the concentrated load P = 70 lb. Suppose that w= 17 lb/ft. Follow the sign convention. Part A Figure 3 ft -1.5 ft √30° 1 of 1 Determine the normal force at point C. Express your answer in pounds to three significant figures. ΜΕ ΑΣΦ Η vec Nc= Submit Request Answer Part B Determine the shear force at point C. Express your answer in pounds to three significant figures. VC= ΜΕ ΑΣΦΗ vec Submit Request Answer Part C Determine the moment at point C. Express your answer in pound-feet to three significant figures. Mc= Ο ΑΣΦ Η vec Submit Request Answer Provide Feedback ? ? lb lb ? lb-ftarrow_forwardConsider a uniformly charged ring of radius R with total charge Q, centered at the origin inthe xy-plane. Find the electric field (as a vector) at a point on the z-axis at a distance z above thecenter of the ring. Assume the charge density is constant along the ring.arrow_forward
- 3) If the slider block C is moving at 3m/s, determine the angular velocity of BC and the crank AB at the instant shown. (Use equation Vs Vc wx fuc, then use equation Vs VA + Ve/athen write it in terms of w and the appropriate r equate the two and solve) 0.5 m B 1 m 60° A 45° vc = 3 m/sarrow_forward3) If the slider block C is moving at 3m/s, determine the angular velocity of BC and the crank AB at the instant shown. (Use equation Vs Vc wxf, then use equation V, VA + Va/Athen write it in terms of w and the appropriate r equate the two and solve) f-3marrow_forwardPls help ASAParrow_forward
- Pls help ASAParrow_forward14. A boy is out walking his dog. From his house, he walks 30 m North, then 23 m East, then 120 cm South, then 95 m West, and finally 10 m East. Draw a diagram showing the path that the boy walked, his total displacement, and then determine the magnitude and direction of his total displacement.arrow_forwardPls help ASAParrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





