Chapter 3, Problem 46P

To determine

To verify the Stokes’s theorem for the given region.

Explanation of Solution

Given:

The vector field $F$ is $2\rho z{a}_{\rho }+3z\sin \varphi a_{\varphi }-4\rho \cos \varphi a_z$.

The open surface is defined by the parameters, $z=1,0<\rho <2,0<\varphi <45°$.

Calculation:

According to the Stokes’s theorem,

  ${\displaystyle \underset{L}{\oint }F\cdot dl}={\displaystyle \underset{S}{\int }\left(\nabla \times F\right)dS}$

Calculate ${\displaystyle \underset{L}{\oint }F\cdot dl}$ along the contour as shown in the below figure.

  ${\displaystyle \underset{L}{\oint }F\cdot dl}={\displaystyle \underset{P}{\int }F\cdot dl+{\displaystyle \underset{Q}{\int }F\cdot dl+{\displaystyle \underset{R}{\int }F\cdot dl}}}$        (I)

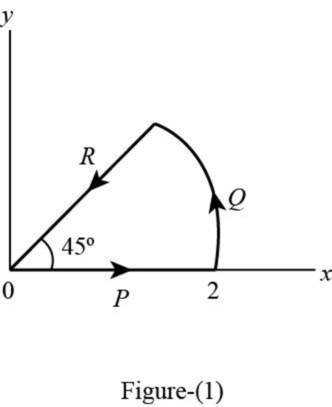
For the segment $P$, $z=1$ and $dl=d\rho a_{\rho }$.

Therefore,

  $\begin{array}{l}F=2\rho z{a}_{\rho }+3z\sin \varphi a_{\varphi }-4\rho \cos \varphi a_z\\ F=2\rho \left(1\right)a_{\rho }+3\left(1\right)\sin \varphi a_{\varphi }-4\rho \cos \varphi a_z\\ F=2\rho a_{\rho }+3\sin \varphi a_{\varphi }-4\rho \cos \varphi a_z\end{array}$

Calculate the integral $\left({\displaystyle \underset{P}{\oint }F\cdot dl}\right)$ in the segment $P$ using the relation.

  $\begin{array}{c}{\displaystyle \underset{P}{\oint }F\cdot dl}={\displaystyle \underset{0}{\overset{2}{\int }}\left(2\rho a_{\rho }+3\sin \varphi a_{\varphi }-4\rho \cos \varphi a_z\right)\cdot \left(d\rho a_{\rho }\right)}\\ {\displaystyle \underset{P}{\oint }F\cdot dl}={\displaystyle \underset{0}{\overset{2}{\int }}2\rho d\rho }\\ {\displaystyle \underset{P}{\oint }F\cdot dl}=2{\left[\frac{{\rho }^2}{2}\right]}_0^2\\ {\displaystyle \underset{P}{\oint }F\cdot dl}=4\end{array}$

For segment $Q$, $\rho =2,z=1\text{and}dl=\rho d\varphi a_{\varphi }$.

Therefore,

  $\begin{array}{l}F=2\rho z{a}_{\rho }+3z\sin \varphi a_{\varphi }-4\rho \cos \varphi a_z\\ F=2\left(2\right)\left(1\right)a_{\rho }+3\left(1\right)\sin \varphi a_{\varphi }-4\left(2\right)\cos \varphi a_z\\ F=4a_{\rho }+3\sin \varphi a_{\varphi }-8\cos \varphi a_z\end{array}$

Calculate the integral $\left({\displaystyle \underset{Q}{\oint }F\cdot dl}\right)$ in the segment $Q$ using the relation.

  $\begin{array}{c}{\displaystyle \underset{Q}{\oint }F\cdot dl}={\displaystyle \underset{0}{\overset{45°}{\int }}\left(4a_{\rho }+3\sin \varphi a_{\varphi }-8\cos \varphi a_z\right)\cdot \left(\rho d\varphi a_{\varphi }\right)}\\ {\displaystyle \underset{Q}{\oint }F\cdot dl}={\displaystyle \underset{0}{\overset{45°}{\int }}3\rho \sin \varphi d\varphi }\\ {\displaystyle \underset{Q}{\oint }F\cdot dl}=3\rho {\left[-\cos \varphi \right]}_0^{45°}\\ {\displaystyle \underset{Q}{\oint }F\cdot dl}=3\times 2\left[-\frac{1}{\sqrt{2}}+1\right]\end{array}$

  ${\displaystyle \underset{Q}{\oint }F\cdot dl}=1.7573$

For segment $R$, $\varphi =45°,z=1\text{and}dl=d\rho a_{\rho }$.

Therefore,

  $\begin{array}{l}F=2\rho z{a}_{\rho }+3z\sin \varphi a_{\varphi }-4\rho \cos \varphi a_z\\ F=2\rho \left(1\right)a_{\rho }+3\left(1\right)\sin \left(45°\right)a_{\varphi }-4\rho \cos \left(45°\right)a_z\\ F=2\rho a_{\rho }+2.12a_{\varphi }-2.82a_z\end{array}$

Calculate the integral $\left({\displaystyle \underset{R}{\oint }F\cdot dl}\right)$ in the segment $R$ using the relation.

  $\begin{array}{c}{\displaystyle \underset{Q}{\oint }F\cdot dl}={\displaystyle \underset{2}{\overset{0}{\int }}\left(2\rho a_{\rho }+2.12a_{\varphi }-2.82a_z\right)\cdot \left(d\rho a_{\rho }\right)}\\ {\displaystyle \underset{Q}{\oint }F\cdot dl}={\displaystyle \underset{2}{\overset{0}{\int }}2\rho d\rho }\\ {\displaystyle \underset{Q}{\oint }F\cdot dl}=2{\left[\frac{{\rho }^2}{2}\right]}_2^0\\ {\displaystyle \underset{Q}{\oint }F\cdot dl}=-4\end{array}$

Calculate the value of integral $\left({\displaystyle \underset{L}{\oint }F\cdot dl}\right)$ using the relation.

  $\begin{array}{l}{\displaystyle \underset{L}{\oint }F\cdot dl}={\displaystyle \underset{P}{\int }F\cdot dl+{\displaystyle \underset{Q}{\int }F\cdot dl+{\displaystyle \underset{R}{\int }F\cdot dl}}}\\ {\displaystyle \underset{L}{\oint }F\cdot dl}=4+1.7573-4\\ {\displaystyle \underset{L}{\oint }F\cdot dl}=1.7573\end{array}$        (I)

Calculate the value of the curl $\left(\nabla \times F\right)$ using the relation.

  $\begin{array}{l}\nabla \times F=\left[\frac{1}{\rho }\frac{\partial \left(F_z\right)}{\partial \varphi }-\frac{\partial F_{\varphi }}{\partial z}\right]a_{\rho }+\left[\frac{\partial F_{\rho }}{\partial z}-\frac{\partial F_z}{\partial \rho }\right]a_{\varphi }+\frac{1}{\rho }\left[\frac{\partial \left(\rho F_{\varphi }\right)}{\partial \rho }-\frac{\partial F_{\rho }}{\partial \varphi }\right]a_z\\ \nabla \times F=\left[\begin{array}{l}\left[\frac{1}{\rho }\frac{\partial \left(-4\rho \cos \varphi \right)}{\partial \varphi }-\frac{\partial \left(3z\sin \varphi \right)}{\partial z}\right]a_{\rho }+\left[\frac{\partial \left(2\rho z\right)}{\partial z}-\frac{\partial \left(-4\rho \cos \varphi \right)}{\partial \rho }\right]a_{\varphi }\\ +\frac{1}{\rho }\left[\frac{\partial \left(\rho \times 3z\sin \varphi \right)}{\partial \rho }-\frac{\partial \left(2\rho z\right)}{\partial \varphi }\right]a_z\end{array}\right]\\ \nabla \times F=\left[\sin \varphi \right]a_{\rho }+\left[2\rho +4\cos \varphi \right]a_{\varphi }+\left[\frac{3z\sin \varphi }{\rho }\right]a_z\end{array}$

Now calculate the integral ${\displaystyle {\int }_{}^{}\left({\displaystyle \underset{S}{\int }\left(\nabla \times F\right)\cdot dS}\right)}$ using the relation.

  $\begin{array}{l}{\displaystyle \underset{S}{\int }\left(\nabla \times F\right)\cdot dS}={\displaystyle \underset{S}{\int }\left(\left[\sin \varphi \right]a_{\rho }+\left[2\rho +4\cos \varphi \right]a_{\varphi }+\left[\frac{3z\sin \varphi }{\rho }\right]a_z\right)}\cdot \left(\rho d\varphi d\rho a_z\right)\\ {\displaystyle \underset{S}{\int }\left(\nabla \times F\right)\cdot dS}={\displaystyle \underset{S}{\int }3z\sin \varphi d\varphi d\rho }\\ {\displaystyle \underset{S}{\int }\left(\nabla \times F\right)\cdot dS}={\displaystyle \underset{\rho =0}{\overset{2}{\int }}{\displaystyle \underset{\varphi =0}{\overset{45°}{\int }}{\left(3z\sin \varphi d\varphi d\rho \right)}_{z=1}}}\\ {\displaystyle \underset{S}{\int }\left(\nabla \times F\right)\cdot dS}=3{\left[-\cos \varphi \right]}_0^{45°}{\left[\rho \right]}_0^2\end{array}$

  ${\displaystyle \underset{S}{\int }\left(\nabla \times F\right)\cdot dS}=1.758$        (II)

From Equations (I) and Equation (II).

  ${\displaystyle \underset{L}{\oint }F\cdot dl}={\displaystyle \underset{S}{\int }\left(\nabla \times F\right)\cdot dS}$

Thus, the Stokes’s theorem is verified.