Excursions in Mathematics, Loose-Leaf Edition Plus MyLab Math with Pearson eText -- 18 Week Access Card Package
9th Edition
ISBN: 9780136208754
Author: Tannenbaum, Peter
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 3, Problem 39E
Exercises 39 and 40 refer to the following: Arthur, Brian, and Carl are dividing the cake shown in Fig. 3-27 using the lone-chooser method. Arthur loves chocolate cake and orange cake equally but hates strawberry cake and vanilla cake. Brian loves chocolate cake and strawberry cake equally but hates orange cake and vanilla cake. Carl loves chocolate cake and vanilla cake equally but hates orange cake and strawberry cake. In your answers, assume all cuts are normal “cake cuts” from the center to the edge of the cake. You can describe each piece of cake by giving the angles of its parts, as in “15° strawberry–40° chocolate” or “60° orange only.”
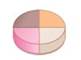
Figure 3-27
39. Suppose that Arthur and Brian are the dividers and Carl is the chooser. In the first division, Arthur cuts the cake vertically through the center as shown in Fig. 3-28 and Brian picks the share he likes better. In the second division, Brian subdivides the share he chose into three pieces and Arthur subdivides the other share into three pieces.
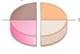
Figure 3-28
a. Describe which share (s or s ) Brian picks and how he might subdivide it.
b. Describe how Arthur might subdivide the other share.
c. Based on the subdivisions in (a) and (b), describe a possible final fair division of the cake.
d. For the final fair division you described in (c), find the value of each share (as a percentage of the total value of the cake) in the eyes of the player receiving it.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
7. Rank and Nullity
•
Prove the Rank-Nullity Theorem: dim(ker(T)) + dim(im(T)) = dim(V) for a linear
transformation T: VW.
•
Compute the rank and nullity of the matrix:
[1 2 37
C
=
45 6
7
8 9
5. Inner Product Spaces
•
•
Prove that the space C[a, b] of continuous functions over [a, b] with the inner product
(f,g) = f f (x)g(x)dx is an inner product space.
Use the Gram-Schmidt process to orthogonalize the vectors (1, 1, 0), (1, 0, 1), and
(0, 1, 1).
19. Block Matrices
• Prove that the determinant of a block matrix:
A B
0 D
.
is det(A) · det (D), where A and D are square matrices.
•
Show how block matrices are used in solving large-scale linear systems.
Chapter 3 Solutions
Excursions in Mathematics, Loose-Leaf Edition Plus MyLab Math with Pearson eText -- 18 Week Access Card Package
Ch. 3 - Henry, Tom, and Fred are breaking up their...Ch. 3 - Alice, Bob, and Carlos are dividing among...Ch. 3 - Angie, Bev, Ceci, and Dina are dividing among...Ch. 3 - Mark, Tim, Maia, and Kelly are dividing among...Ch. 3 - Allen, Brady, Cody, and Diane are sharing a cake....Ch. 3 - Carlos, Sonya, Tanner, and Wen are sharing a cake....Ch. 3 - Four partners Adams, Benson, Cagle, and Duncan...Ch. 3 - Prob. 8ECh. 3 - Suppose that Angelina values strawberry cake twice...Ch. 3 - Suppose that Brad values chocolate cake thrice as...
Ch. 3 - Suppose that Brad values chocolate cake four as...Ch. 3 - Suppose that Angelina values strawberry cake five...Ch. 3 - Karla and five other friends jointly buy the...Ch. 3 - Marla and five other friends jointly buy the...Ch. 3 - Suppose that they flip a coin and Jackie ends up...Ch. 3 - Suppose they flip a coin and Karla ends up being...Ch. 3 - Suppose that they flip a coin and Martha ends up...Ch. 3 - Suppose that they flip a coin and Nick ends up...Ch. 3 - Suppose that David is the divider and Paula is the...Ch. 3 - Suppose that Paula is the divider and David is the...Ch. 3 - Three partners are dividing a plot of land among...Ch. 3 - Three partners are dividing a plot of land among...Ch. 3 - Four partners are dividing a plot of land among...Ch. 3 - Four partners are dividing a plot of land among...Ch. 3 - Mark, Tim, Maia, and Kelly are dividing a cake...Ch. 3 - Allen, Brady, Cody; and Diane are sharing a cake...Ch. 3 - Prob. 27ECh. 3 - Four partners are dividing a plot of land among...Ch. 3 - Prob. 29ECh. 3 - Five players are dividing a cake among themselves...Ch. 3 - Four partners Egan, Fine, Gong, and Hart jointly...Ch. 3 - Four players Abe, Betty, Cory, and Dana are...Ch. 3 - Exercises 33 and 34 refer to the following...Ch. 3 - Exercises 33 and 34 refer to the following...Ch. 3 - Exercise 35 through 38 refer to the following...Ch. 3 - Exercise 35 through 38 refer to the following...Ch. 3 - Prob. 37ECh. 3 - Prob. 38ECh. 3 - Exercises 39 and 40 refer to the following:...Ch. 3 - Exercises 39 and 40 refer to the following:...Ch. 3 - Jackie, Karla, and Lori are dividing the foot-long...Ch. 3 - Jackie, Karla, and Lori are dividing the foot-long...Ch. 3 - Ana, Belle, and Chloe are dividing four pieces of...Ch. 3 - Andre, Bea, and Chad are dividing an estate...Ch. 3 - Five heirs A,B,C,D, and E are dividing an estate...Ch. 3 - Oscar, Bert, and Ernie are using the method of...Ch. 3 - Anne, Bette, and Chia jointly own a flower shop....Ch. 3 - Al, Ben and Cal jointly own a fruit stand. They...Ch. 3 - Ali, Briana, and Caren are roommates planning to...Ch. 3 - Anne, Bess and Cindy are the roommates planning to...Ch. 3 - Prob. 51ECh. 3 - Three players (A,B and C) are dividing the array...Ch. 3 - Three players (A,B,andC) are dividing the array of...Ch. 3 - Three players (A,B,andC) are dividing the array of...Ch. 3 - Five players (A,B,C,D,andE) are dividing the array...Ch. 3 - Four players (A,B,C,andD) are dividing the array...Ch. 3 - Prob. 57ECh. 3 - Queenie, Roxy, and Sophie are dividing a set of 15...Ch. 3 - Ana, Belle, and Chloe are dividing 3 Choko bars, 3...Ch. 3 - Prob. 60ECh. 3 - Prob. 61ECh. 3 - Prob. 62ECh. 3 - Prob. 63ECh. 3 - Prob. 64ECh. 3 - Three players A, B, and C are sharing the...Ch. 3 - Angeline and Brad are planning to divide the...Ch. 3 - Prob. 67ECh. 3 - Efficient and envy-free fair divisions. A fair...Ch. 3 - Suppose that N players bid on M items using the...Ch. 3 - Asymmetric method of sealed bids. Suppose that an...Ch. 3 - Prob. 73E
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 6. Norms and Metrics • Show that the function || || norm on Rn. = √xT Ax, where A is a positive definite matrix, defines a . Prove that the matrix norm induced by the vector L²-norm satisfies ||A||2 ✓ max (ATA), where Amax is the largest eigenvalue.arrow_forward2. Linear Transformations • • Let T: R3 R³ be a linear transformation such that T(x, y, z) = (x + y, y + z, z + → x). Find the matrix representation of T with respect to the standard basis. Prove that a linear transformation T : VV is invertible if and only if it is bijective.arrow_forward11. Positive Definiteness Prove that a matrix A is positive definite if and only if all its eigenvalues are positive.arrow_forward
- 21. Change of Basis Prove that the matrix representation of a linear transformation T : V → V depends on the choice of basis in V. If P is a change of basis matrix, show that the transformation matrix in the new basis is P-¹AP.arrow_forward14. Projection Matrices Show that if P is a projection matrix, then P² = P. Find the projection matrix onto the subspace spanned by the vector (1,2,2)T.arrow_forward4. Diagonalization Prove that a square matrix A is diagonalizable if and only if A has n linearly independent eigenvectors. • Determine whether the following matrix is diagonalizable: [54 2 B = 01 -1 3arrow_forward
- 8. Determinants • • Prove that the determinant of a triangular matrix is the product of its diagonal entries. Show that det(AB) = det(A)det(B) for any two square matrices A and B.arrow_forward15. Tensor Products • • Define the tensor product of two vector spaces. Compute the tensor product of (1,0) and (0, 1) in R². Discuss the role of tensors in multilinear algebra and provide an example of a second-order tensor.arrow_forward20. Numerical Methods • Describe the QR decomposition method and explain its use in solving linear systems. • Solve the following system numerically using Jacobi iteration: 10x+y+z = 12, 2x+10y+z = 13, 2x+2y+10z = 14.arrow_forward
- 1. Vector Spaces • Prove that the set of all polynomials of degree at most n forms a vector space over R. Determine its dimension. • = Let VR³ and define a subset W = {(x, y, z) Є R³ | x + y + z = 0}. Prove that W is a subspace of V and find its basis.arrow_forward24. Spectral Decomposition Explain the spectral decomposition of a symmetric matrix and its applications. • Compute the spectral decomposition of: A = 5 4arrow_forward3. Eigenvalues and Eigenvectors • Find the eigenvalues and eigenvectors of the matrix: 2 1 A = = Prove that if A is a symmetric matrix, then all its eigenvalues are real.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Mod-01 Lec-01 Discrete probability distributions (Part 1); Author: nptelhrd;https://www.youtube.com/watch?v=6x1pL9Yov1k;License: Standard YouTube License, CC-BY
Discrete Probability Distributions; Author: Learn Something;https://www.youtube.com/watch?v=m9U4UelWLFs;License: Standard YouTube License, CC-BY
Probability Distribution Functions (PMF, PDF, CDF); Author: zedstatistics;https://www.youtube.com/watch?v=YXLVjCKVP7U;License: Standard YouTube License, CC-BY
Discrete Distributions: Binomial, Poisson and Hypergeometric | Statistics for Data Science; Author: Dr. Bharatendra Rai;https://www.youtube.com/watch?v=lHhyy4JMigg;License: Standard Youtube License