Chapter 3, Problem 3.5.4P

To determine

(a)

The maximum factored load using Load and Resistance Factor Design (LRFD).

Answer to Problem 3.5.4P

The maximum factored load using LRFD is $125.789\text{kips}$.

Explanation of Solution

Given:

The following figure shows the A36 steel connection with $\frac{3}{4}\text{in}$ bolts.

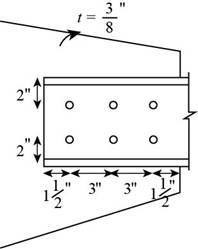
Figure-(1)

Concept Used:

Write the expression for the factored strength in yielding.

$P_{\text{y}}={\Phi }_{\text{y}}\times P_{\text{ny}}$ …… (I)

Write the expression for the factored strength in rupture.

$P_{\text{r}}={\Phi }_{\text{f}}\times P_{\text{nf}}$ …… (II)

Here, the factored yielding strength of the material is $P_{\text{y}}$, the factored strength in rupture is $P_{\text{r}}$, the resistance factor for yielding is ${\Phi }_{\text{y}}$, the resistance factor for rupture is ${\Phi }_{\text{f}}$, the nominal strength in yielding is $P_{\text{ny}}$ and the nominal strength in rupture is $P_{\text{nr}}$.

Write the expression for block shear.

$R_{\text{u}}=0.6F_{\text{u}}{A}_{\text{nv}}+U_{\text{bs}}{F}_{\text{u}}{A}_{\text{nt}}$ …… (III)

Write the expression for the upper limit of block shear.

$UL=0.6F_{\text{y}}{A}_{\text{gv}}+U_{\text{bs}}{F}_{\text{u}}{A}_{\text{nt}}$ …… (IV)

Here, the upper limit is $UL$, the block shear is $R_{\text{u}}$, the ultimate stress is $F_{\text{u}}$, the yield stress is $0.6F_{\text{y}}$, the factor for tension stress is $U_{\text{bs}}$, the gross area along the shear surface is $A_{\text{gv}}$, the net area along the shear surface is $A_{\text{nv}},$ and the net area along the tension surface is $A_{\text{nt}}$ .The design strength of LRFD is the minimum of Equation (I) and (II).

Write the expression for the design block shear strength.

$P=R\Phi$ …… (V)

Here the design block shear strength, the minimum of Equation (III) and (IV), is $R$ and the resistance factor is $\Phi$.

The maximum factored load is the minimum of Equation (I), (II), and (V).

Write the expression for the nominal strength in yielding for the tension member.

$P_{\text{ny}}=F_{\text{y}}\times A_{\text{g}}$ …… (VI)

Here, the yield strength in yielding is $F_{\text{y}}$, the gross area of the gross member is $A_{\text{g}}$.

Write the expression for the nominal strength in rupture for the tension member.

$P_{\text{nf}}=F_{\text{u}}\times A_{\text{e}}$ …… (VII)

Here, the yield strength in rupture is $F_{\text{u}}$, the effective area is $A_{\text{e}}$.

Write the expression for the effective area.

$A_{\text{e}}=A_{\text{n}}U$ …… (VIII)

Here, the area reduction factor is $U$, the effective area is $A_{\text{e}}$, the net area is $A_{\text{n}}$

Write the expression for the area reduction factor.

$U=1-\frac{\overline{x}}{l}$ …… (IX)

Here the distance from the centroid of the connected area $\overline{x}$ and the length of the connection is $l$.

Write the expression for the net area of the tension member.

$A_{\text{n}}=A_{\text{g}}-t\times d_{\text{holes}}$ …… (X)

Here, the thickness of the tension member is $t$, the diameter of holes is $d_{\text{holes}}$.

Write the expression for the diameter of the holes.

$d_{\text{holes}}=d+\frac{1}{8}\text{in}$ …… (XI)

Here the diameter of the bolts is $d$ and $\frac{3}{16}\text{in}$ is the allowance for side clearance for bolts greater than $1\text{in}$.

Calculation:

Calculate the nominal shear strength of the tension member in yielding.

Substitute $50\text{ksi}$ for $F_{\text{y}}$ and $3.60{\text{in}}^2$ for $A_{\text{g}}$ in the Equation (VI).

$\begin{array}{c}{P}_{\text{ny}}=50\text{ksi}\times \text{3}\text{.60}{\text{in}}^2\\ =180\text{kips}\end{array}$

Calculate the diameter of the holes.

Substitute $\frac{3}{4}\text{in}$ for $d$ in the Equation (XI).

$\begin{array}{c}{d}_{\text{holes}}=\frac{3}{4}\text{in}+\frac{1}{8}\text{in}\\ =0.\text{875}\text{in}\end{array}$

Calculate the net area of the tension member.

Substitute $3.60{\text{in}}^2$ for $A_{\text{g}}$ and $0.875\text{in}$ for $d_{\text{holes}}$ in the Equation (X).

$\begin{array}{c}{A}_{\text{n}}=3.60{\text{in}}^2-2\times \left(0.314\times 0.875\right){\text{in}}^2\\ =3.60-2\times 0.278\\ =3.60-2\times 0.550\\ =3.051{\text{in}}^2\end{array}$

Calculate the length of the connection.

$\begin{array}{c}l=3\text{in}+\text{3}\text{in}\\ =\text{6}\text{in}\end{array}$

Calculate the area reduction factor.

Substitute $6\text{in}$ for $l$ and $0.525\text{in}$ for $\overline{x}$ in the Equation (IX).

$\begin{array}{c}U=1-\frac{0.525\text{in}}{6\text{in}}\\ =1-0.088\\ =0.913\end{array}$

Calculate the effective area of the member.

Substitute $3.051{\text{in}}^2$ for $A_{\text{n}}$ and $0.913$ for $U$ in Equation (VIII).

$\begin{array}{c}{A}_{\text{e}}=\left(3.051{\text{in}}^2\right)\times 0.913\\ =2.784{\text{in}}^2\end{array}$

Calculate the nominal shear strength of the tension member in rupture.

Substitute $65\text{ksi}$ for $F_{\text{u}}$ and $2.784{\text{in}}^2$ for $A_{\text{e}}$ in the Equation (VII).

$\begin{array}{c}{P}_{\text{nf}}=\left(65\text{ksi}\right)\times \left(\text{2}\text{.784}{\text{in}}^2\right)\\ =180.963\text{kips}\end{array}$

Calculate the net area along the shear surface of the tension member.

$\begin{array}{c}{A}_{\text{n}}=0.314{\text{in}}^2\left[2\times \left(1\frac{1}{2}+3+3\right)\text{in}-2\times \left(2.5\times 0.875\right)\text{in}\right]\\ =0.314\left[15-4.375\right]{\text{in}}^2\\ =0.314\left[10.625\right]{\text{in}}^2\\ =3.336{\text{in}}^2\end{array}$

Calculate the net area along the tension surface of the tension member.

$\begin{array}{c}{A}_{\text{nt}}=0.314\times 3{\text{in}}^2-2\times 0.314\times 0.5\left(\frac{3}{4}+\frac{1}{8}\right){\text{in}}^2\\ =0.942{\text{in}}^2-0.314\times 0.875{\text{in}}^2\\ =0.942{\text{in}}^2-0.278{\text{in}}^2\\ =0.667{\text{in}}^2\end{array}$

Calculate the gross area along the shear surface in the gusset plate.

$\begin{array}{c}{A}_{\text{gv}}=2\times \left(\frac{3}{8}\text{in}\times \left(1\frac{1}{2}\text{in}+3\text{in+3}\text{in}\right)\right)\\ =2\times \left(\frac{3}{8}\text{in}\times 7.5\text{in}\right)\\ =2\times 2.813{\text{in}}^2\\ =5.625{\text{in}}^2\end{array}$

Calculate the net area along the shear surface of the gusset plate.

$\begin{array}{c}{A}_{\text{nv}}=2\times \left[\frac{3}{8}\text{in}\times \left(1\frac{1}{2}\text{in}+3\text{in+3}\text{in}\right)-\frac{3}{8}\text{in}\left(2.5\times \left(\frac{3}{4}+\frac{1}{8}\right)\text{in}\right)\right]\\ =2\times \left[\frac{3}{8}\text{in}\times \left(7.5\text{in}\right)-\frac{3}{8}\text{in}\left(2.5\times 0.875\right)\right]\\ =2\times \left[2.813{\text{in}}^2\text{-}\frac{3}{8}\times 2.188{\text{in}}^2\right]\\ =2\times \left[2.813{\text{in}}^2-0.820{\text{in}}^2\right]\end{array}$

Substitute further.

$\begin{array}{c}{A}_{\text{nv}}=2\times 1.993{\text{in}}^2\\ =3.985{\text{in}}^2\end{array}$

Calculate the net area along the tension surface of the gusset plate.

$\begin{array}{c}{A}_{\text{nt}}=\frac{3}{8}\text{in}\times \left(3-2\times 0.5\times \left(\frac{3}{4}+\frac{1}{8}\right)\right)\text{in}\\ =\frac{3}{8}\text{in}\times \left[3-0.875\right]\text{in}\\ =\frac{3}{8}\times 2.125{\text{in}}^2\\ =0.797{\text{in}}^2\end{array}$

Calculate the shear strength for the tension member.

Substitute $3.336{\text{in}}^2$ for $A_{\text{nv}}$, $0.667{\text{in}}^2$ for $A_{\text{nt}}$, $65\text{ksi}$ for $F_{\text{u}}$ and $1$ for $U_{\text{bs}}$ in Equation (III).

$\begin{array}{c}{R}_{\text{u}}=\left(0.6\times 65\text{ksi}\times 3.336{\text{in}}^2\right)+\left(1\times 65\times 0.667{\text{in}}^2\right)\\ =130.104\text{kips}+43.355\text{kips}\\ =173.459\text{kips}\end{array}$

Calculate the upper limit.

Substitute $0.667{\text{in}}^2$ for $A_{\text{nt}}$

$4.71{\text{in}}^2$ for $A_{\text{gv}}$, $50\text{ksi}$ for $F_{\text{y}}$, $65\text{ksi}$ for $F_{\text{u}}$ and $1$ for $U_{\text{bs}}$ in the Equation(IV).

$\begin{array}{c}UL=0.6\times \left(50\text{ksi}\right)\times \left(4.71{\text{in}}^2\right)+1\times \left(65\text{ksi}\right)\times \left(0.667{\text{in}}^2\right)\\ =141.3\text{kips}+43.355\text{kips}\\ =184.655\text{kips}\end{array}$

The value of the shear is larger than the upper limit. Hence, it is not feasible.

Adopt the shear strength of the tension member to be $173.459\text{kips}$.

Calculate the shear strength for the gusset plate.

Substitute $3.985{\text{in}}^2$ for $A_{\text{nv}}$, $0.797{\text{in}}^2$ for $A_{\text{nt}}$, $58\text{ksi}$ for $F_{\text{u}},$ and $1$ for $U_{\text{bs}}$ in the Equation (III)

$\begin{array}{c}{R}_{\text{u}}=\left(0.6\times 58\text{ksi}\times 3.985{\text{in}}^2\right)+\left(1\times 58\times 0.797{\text{in}}^2\right)\\ =136.678\text{kips}+46.219\text{kips}\\ =184.897\text{kips}\end{array}$

Calculate the upper limit

Substitute $0.797{\text{in}}^2$ for $A_{\text{nt}}$

$5.625{\text{in}}^2$ for $A_{\text{gv}}$, $36\text{ksi}$ for $F_{\text{y}}$, $58\text{ksi}$ for $F_{\text{u}}$ and $1$ for $U_{\text{bs}}$ in the Equation (IV).

$\begin{array}{c}UL=0.6\times \left(36\text{ksi}\right)\times \left(5.625{\text{in}}^2\right)+1\times \left(58\text{ksi}\right)\times \left(0.797{\text{in}}^2\right)\\ =121.5\text{kips}+46.219\text{kips}\\ =167.719\text{kips}\end{array}$

The value of the shear is larger than the upper limit. Hence, it is not feasible.

Adopt the shear strength of the gusset plate to be $167.719\text{kips}$.

Compare the shear strength of the tension member and that of the gusset plate.

Thus the block shear strength is $167.719\text{kips}$.

Calculate the design block shear strength of the connection.

Calculate the factored yielding strength.

Substitute $0.90$ for ${\Phi }_{\text{y}}$ and $180\text{kips}$ for $P_{\text{ny}}$ in the Equation (I).

$\begin{array}{c}{P}_{\text{y}}=0.90\times 180\text{kips}\\ =162\text{kips}\end{array}$

Calculate the factored rupture strength.

Substitute $0.75$ for ${\Phi }_{\text{y}}$ and $180.963\text{kips}$ for $P_{\text{ny}}$ in the Equation (I).

$\begin{array}{c}{P}_{\text{r}}=0.75\times 180.963\text{kips}\\ =135.722\text{kips}\end{array}$

Calculate the factored strength of block shear.

Substitute $167.719\text{kips}$ for $R_{\text{u}}$ and $0.75$ for $\Phi$ in the Equation (V).

$\begin{array}{c}P=\left(167.719\text{kips}\right)\times \text{0}\text{.75}\\ \text{=125}\text{.789}\text{kips}\end{array}$

Conclusion:

Thus, the maximum factored load is $125.789\text{kips}$.

To determine

(b)

The allowable block shear strength of the connection.

Answer to Problem 3.5.4P

The allowable block shear strength of the connection is $83.860\text{kips}$.

Explanation of Solution

Concept used:

Write the expression for the factored design block shear strength.

$P_{\text{a}}=\frac{R_{\text{u}}}{\Omega }$ …… (XII)

Here the safety factor is $\Omega$, the allowable block shear strength value is $P_{\text{a}}$.

Calculation:

Calculate the allowable block shear strength of the connection.

Calculate the allowable yielding strength.

Substitute $2$ for $\Omega$ and $180\text{kips}$ for $R_{\text{u}}$ in the Equation (XII).

$\begin{array}{c}{P}_{\text{a}}=\frac{180}{2}\\ =90\text{kips}\end{array}$

Calculate the allowable rupture strength.

Substitute $2$ for $\Omega$ and $180.963\text{kips}$ for $R_{\text{u}}$ in the Equation (XII).

$\begin{array}{c}{P}_{\text{a}}=\frac{180.963}{2}\\ =90.482\text{kips}\end{array}$

Calculate the factored strength of block shear.

Substitute $167.719\text{kips}$ for $R_{\text{u}}$ and $2$ for $\Omega$ in the Equation (XII).

$\begin{array}{c}{P}_{\text{a}}=\frac{167.719\text{kips}}{2}\\ =83.\text{860}\text{kips}\end{array}$

Conclusion:

Thus, the maximum allowable block shear strength of the connection is $83.860\text{kips}$.