Chapter 3, Problem 1RE

In Exercises 1–6, graph the given equations and determine how many solutions the system has, if any.

$\begin{array}{c}x+2y=4\\ 2x-y=1\end{array}$

To determine

To graph: The system of equations consisting of $x+2y=4$ and $2x-y=1$. Also, determine the number of solutions the system has, if any.

Explanation of Solution

Given Information:

The system of equations is;

$\begin{array}{c}x+2y=4\\ 2x-y=1\end{array}$

Graph:

Consider the equations,

$\begin{array}{c}x+2y=4\\ 2x-y=1\end{array}$

Rewrite the given equations,

$\begin{array}{c}y=-\frac{x}{2}+2\\ y=2x-1\end{array}$

Use the graphing calculator to determine the solution of the given system of equation,

Step 1: In the TI-83 calculator press the ON key.

Step 2: Click on the $\boxed{\text{Y}=}$ button.

Step 3: Write the desired equation in $Y_1$ and $Y_2$ as follows:

$\begin{array}{l}{\text{Y}}_{\text{1}}=-\frac{\text{X}}{2}+2\\ {\text{Y}}_{\text{2}}=2\text{X}-1\end{array}$

Step 4: Press the $\boxed{\text{WINDOW}}$ button and set the window as;

${\text{X}}_{\min }=-10,{\text{X}}_{\max }=10,X_{scl}=5,{\text{Y}}_{\min }=-5,{\text{Y}}_{\max }=5,Y_{scl}=5$

Step 5: Press the $\boxed{\text{GRAPH}}$ button to get the graph.

The graph is shown below;

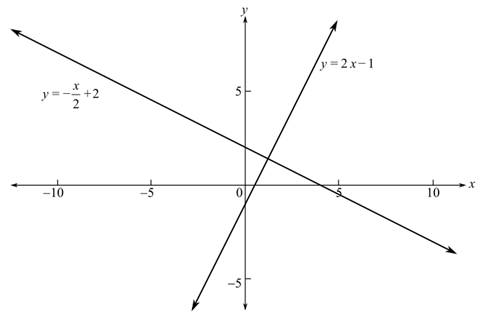
From the graph, it can be observed that the graphs of the system of equation intersect at a single point.

Interpretation:

As the graphs of the equation intersect at a single point there is a unique solution for the given system of equation.