
Concept explainers
Simulate five sample trajectories of Eq.
Hint: For the
Equation
where
The five sample trajectories of the equation
Answer to Problem 1P
Solution:
The five sample trajectories for
The five sample trajectories for
For
Explanation of Solution
Given information:
The discrete model for change in the price of a stock over a time interval
The parameter values are
Highly volatile have a large value for
A sequence of numbers
Explanation:
The discrete model for change in the price of a stock over a time interval
Where
The parameter values are
Substitute the above values in the equation (1)
Here,
Thus, equation (1) becomes,
Now, to find the value of
By using the computer technology,
For
Substitute the values in equation (2)
For
Substitute the values in equation (2)
For
Substitute the values in equation (2)
For
Substitute the values in equation (2)
For
Substitute the values in equation (2)
Hence, the graph of trajectories for
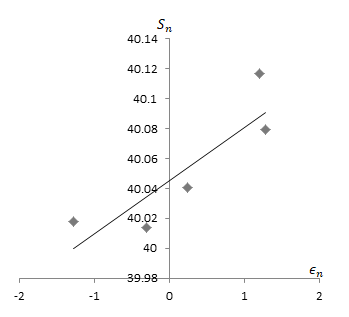
Now, for the value
Here,
Thus, equation (1) becomes,
Now, to find the value of
By using computer technology,
For
Substitute the values in equation (3)
For
Substitute the values in equation (3)
For
Substitute the values in equation (3)
For
Substitute the values in equation (2)
For
Substitute the values in equation (3)
The graph of trajectories for
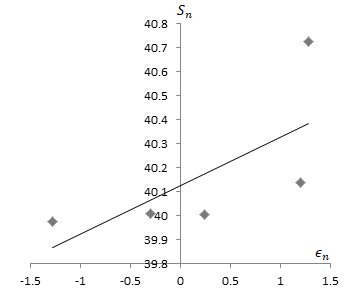
Since the approximation in the graph of trajectories for
Therefore, for
Want to see more full solutions like this?
Chapter 2 Solutions
Differential Equations: An Introduction to Modern Methods and Applications
Additional Math Textbook Solutions
Algebra and Trigonometry (6th Edition)
Calculus: Early Transcendentals (2nd Edition)
Introductory Statistics
Probability And Statistical Inference (10th Edition)
University Calculus: Early Transcendentals (4th Edition)
- II Consider the following data matrix X: X1 X2 0.5 0.4 0.2 0.5 0.5 0.5 10.3 10 10.1 10.4 10.1 10.5 What will the resulting clusters be when using the k-Means method with k = 2. In your own words, explain why this result is indeed expected, i.e. why this clustering minimises the ESS map.arrow_forwardX Acellus | Student admin192c.acellus.com go 0:0 Hannah wants to have concrete stairs for her backdoor. How much concrete will be needed to build the stairs? 20 cm 70 cm 30 cm 15 cm 10 cm 45 cm cm 70 cm GIF 自 لاarrow_forwardwhy the answer is 3 and 10?arrow_forward
- 1 Hannah wants to have concrete stairs for her backdoor. How much concrete will be needed to build the stairs? 70 cm 30 cm 15 cm 10 cm 10 cm 20 cm 45 cm cm³ GIF GIF/ 2 3 4 qwe asdf 5 6 自 yu ty u 8 ghjk 9 P Z X C cv b vbnm ×arrow_forwardPS 9 Two films are shown on screen A and screen B at a cinema each evening. The numbers of people viewing the films on 12 consecutive evenings are shown in the back-to-back stem-and-leaf diagram. Screen A (12) Screen B (12) 8 037 34 7 6 4 0 534 74 1645678 92 71689 Key: 116|4 represents 61 viewers for A and 64 viewers for B A second stem-and-leaf diagram (with rows of the same width as the previous diagram) is drawn showing the total number of people viewing films at the cinema on each of these 12 evenings. Find the least and greatest possible number of rows that this second diagram could have. TIP On the evening when 30 people viewed films on screen A, there could have been as few as 37 or as many as 79 people viewing films on screen B.arrow_forwardskip A swimming pool plan has concrete stairs leading down into the shallow end How much concrete will be needed to build the stairs? Bift 9 ft 2 ft 1 ft 9 ft 2 ft 5 ft [ ? ] ft³arrow_forward

 Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning





