Chapter 2.P3, Problem 1P

Simulate five sample trajectories of Eq. $\left(1\right)$ for the following parameter values and plot the trajectories on the same set of coordinate axes: $\mu =0.12,\sigma =0.1,T=1,s=\$40,N=254$. Then repeat the experiment using the value $\sigma =0.25$ for the volatility. Do the sample trajectories generated in the latter case appear to exhibit a greater degree of variability in their behaviour?

Hint: For the ${\epsilon }_n$’s it is permissible to use a random number generator that creates normally distributed random numbers with mean $0$ and variance $1$.

Equation $\left(1\right)$: The discrete model for change in the price of a stock over a time interval $\left[0,T\right]$ is

$\begin{array}{ccc}{S}_{n+1}=S_n+\mu S_n\Delta t+\sigma S_n{\in }_{n+1}\sqrt{\Delta t},& & S_0=s\end{array},$

where $S_n=S\left(t_n\right)$ is the stock price at time $t_n=n\Delta t,n=0,...,N-1,\Delta t=T/N\text{},\mu$ is the annual growth rate of the stock, and $\sigma$ is a measure of the stock’s annual price volatility or tendency to fluctuate.

To determine

The five sample trajectories of the equation $S_{n+1}=S_n+\mu S_n\Delta t+\sigma S_n{\in }_{n+1}\sqrt{\Delta t},S_0=s$ over the time interval $\left[0,T\right]$ and plot the trajectories on the same set of coordinate axes, where the parameter values are $\mu =0.12,\sigma =0.1,T=1,s=\$40,N=254$ and repeat the experiment using the value $\sigma =0.25$ also determine whether the sample trajectories for $\sigma =0.25$ has a greater degree of variability or not as compared to $\sigma =0.1$.

Answer to Problem 1P

Solution:

The five sample trajectories for $\sigma =0.1$ is

$S_1=40.014117,S_2=40.017659,S_3=40.04040,S_4=40.07913$ and $S_5=40.1167$.

The five sample trajectories for $\sigma =0.25$ is

$S_1=40.007,S_2=39.97596,S_3=40.004,S_4=40.072587$ and $S_5=40.13822$.

For $\sigma =0.25$, the degree of variability is greater than the degree of variability for $\sigma =0.1$.

Explanation of Solution

Given information:

The discrete model for change in the price of a stock over a time interval $\left[0,T\right]$ is $S_{n+1}=S_n+\mu S_n\Delta t+\sigma S_n{\in }_{n+1}\sqrt{\Delta t},S_0=s$, where $S_n=S\left(t_n\right)$ is the stock price at time $t_n=n\Delta t,n=0,...,N-1,\Delta t=T/N\text{},\mu$ is the annual growth rate of the stock, and $\sigma$ is a measure of the stock’s annual price volatility.

The parameter values are $\mu =0.12,\sigma =0.1,T=1,s=\$40,N=254$.

Highly volatile have a large value for $\sigma$.

A sequence of numbers ${\in }_n$ can easily be created by using one of the random number generators.

Explanation:

The discrete model for change in the price of a stock over a time interval $\left[0,T\right]$ is $S_{n+1}=S_n+\mu S_n\Delta t+\sigma S_n{\in }_{n+1}\sqrt{\Delta t},S_0=s$ (1)

Where $S_n=S\left(t_n\right)$ is the stock price at time $t_n=n\Delta t,n=0,...,N-1,\Delta t=T/N\text{}$.

The parameter values are $\mu =0.12,\sigma =0.1,T=1,s=\$40,N=254$.

Substitute the above values in the equation (1)

$\Rightarrow S_{n+1}=S_n+0.12S_n\Delta t+0.1S_n{\in }_{n+1}\sqrt{\Delta t}$.

Here, $\Delta t=T/N\text{}$

$\Rightarrow \Delta t=1/254\text{}=0.0039$.

Thus, equation (1) becomes,

$S_{n+1}=S_n+0.12S_n\times 0.0039+0.1S_n{\in }_{n+1}\times 0.0039$

$S_{n+1}=S_n+0.00047S_n+0.00039S_n{\in }_{n+1}$

$S_{n+1}=1.00047S_n+0.00039S_n{\in }_{n+1}$ ... (2)

Now, to find the value of ${\in }_n$ for five sample trajectories,

By using the computer technology,

For $n=0,{\in }_1=-0.30023$

Substitute the values in equation (2)

$\Rightarrow S_{0+1}=1.00047S_0+0.00039S_0{\in }_{0+1}$

$\Rightarrow S_1=1.00047s+0.00039s{\in }_1$

$\Rightarrow S_1=1.00047\times 40+0.00039\times 40\times \left(-0.30023\right)$

$\Rightarrow S_1=40.0188-0.004683$

$\Rightarrow S_1=40.014117$.

For $n=1,{\in }_2=-1.27768$

Substitute the values in equation (2)

$\Rightarrow S_{1+1}=1.00047S_1+0.00039S_1{\in }_{1+1}$

$\Rightarrow S_2=1.00047S_1+0.00039S_1{\in }_2$

$\Rightarrow S_2=1.00047\times 40.0188+0.00039\times 40.0188\times \left(-1.27768\right)$

$\Rightarrow S_2=40.0376-0.019941$

$\Rightarrow S_2=40.017659$.

For $n=2,{\in }_3=0.244257$

Substitute the values in equation (2)

$\Rightarrow S_{2+1}=1.00047S_2+0.00039S_2{\in }_{2+1}$

$\Rightarrow S_3=1.00047S_2+0.00039S_2{\in }_3$

$\Rightarrow S_3=1.00047\times 40.017659+0.00039\times 40.017659\times \left(0.244257\right)$

$\Rightarrow S_3=40.0365+0.0038121$

$\Rightarrow S_3=40.04040$.

For $n=3,{\in }_4=1.276474$

Substitute the values in equation (2)

$\Rightarrow S_{3+1}=1.00047S_3+0.00039S_3{\in }_{3+1}$

$\Rightarrow S_4=1.00047S_3+0.00039S_3{\in }_4$

$\Rightarrow S_4=1.00047\times 40.04040+0.00039\times 40.04040\times \left(1.276474\right)$

$\Rightarrow S_4=40.0592+0.019933$

$\Rightarrow S_4=40.07913$.

For $n=4,{\in }_5=1.19835$

Substitute the values in equation (2)

$\Rightarrow S_{4+1}=1.00047S_4+0.00039S_4{\in }_{4+1}$

$\Rightarrow S_5=1.00047S_4+0.00039S_4{\in }_5$

$\Rightarrow S_5=1.00047\times 40.07913+0.00039\times 40.07913\times \left(1.19835\right)$

$\Rightarrow S_5=40.09797+0.018731$

$\Rightarrow S_5=40.1167$.

Hence, the graph of trajectories for $\sigma =0.1$ as shown in below figure:

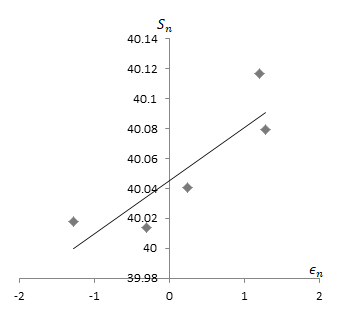
Now, for the value $\sigma =0.25$,

$\Rightarrow S_{n+1}=S_n+0.12S_n\Delta t+0.25S_n{\in }_{n+1}\sqrt{\Delta t}$.

Here, $\Delta t=T/N\text{}$

$\Rightarrow \Delta t=1/254\text{}=0.0039$.

Thus, equation (1) becomes,

$S_{n+1}=S_n+0.12S_n\times 0.0039+0.25S_n{\in }_{n+1}\times 0.0039$

$S_{n+1}=S_n+0.00047S_n+0.000975S_n{\in }_{n+1}$

$S_{n+1}=1.00047S_n+0.000975S_n{\in }_{n+1}$ ... (3)

Now, to find the value of ${\in }_n$ for five sample trajectories,

By using computer technology,

For $n=0,{\in }_1=-0.30023$

Substitute the values in equation (3)

$\Rightarrow S_{0+1}=1.00047S_0+0.000975S_0{\in }_{0+1}$

$\Rightarrow S_1=1.00047s+0.000975s{\in }_1$

$\Rightarrow S_1=1.00047\times 40+0.000975\times 40\times \left(-0.30023\right)$

$\Rightarrow S_1=40.0188-0.0117$

$\Rightarrow S_1=40.007$.

For $n=1,{\in }_2=-1.27768$

Substitute the values in equation (3)

$\Rightarrow S_{1+1}=1.00047S_1+0.000975S_1{\in }_{1+1}$

$\Rightarrow S_2=1.00047S_1+0.000975S_1{\in }_2$

$\Rightarrow S_2=1.00047\times 40.007+0.000975\times 40.007\times \left(-1.27768\right)$

$\Rightarrow S_2=40.0258-0.049838$

$\Rightarrow S_2=39.97596$.

For $n=2,{\in }_3=0.244257$

Substitute the values in equation (3)

$\Rightarrow S_{2+1}=1.00047S_2+0.000975S_2{\in }_{2+1}$

$\Rightarrow S_3=1.00047S_2+0.000975S_2{\in }_3$

$\Rightarrow S_3=1.00047\times 39.97596+0.000975\times 39.97596\times \left(0.244257\right)$

$\Rightarrow S_3=39.9947+0.00952$

$\Rightarrow S_3=40.004$.

For $n=3,{\in }_4=1.276474$

Substitute the values in equation (2)

$\Rightarrow S_{3+1}=1.00047S_3+0.000975S_3{\in }_{3+1}$

$\Rightarrow S_4=1.00047S_3+0.000975S_3{\in }_4$

$\Rightarrow S_4=1.00047\times 40.004+0.000975\times 40.004\times \left(1.276474\right)$

$\Rightarrow S_4=40.0228+0.049787$

$\Rightarrow S_4=40.072587$.

For $n=4,{\in }_5=1.19835$

Substitute the values in equation (3)

$\Rightarrow S_{4+1}=1.00047S_4+0.000975S_4{\in }_{4+1}$

$\Rightarrow S_5=1.00047S_4+0.000975S_4{\in }_5$

$\Rightarrow S_5=1.00047\times 40.072587+0.000975\times 40.072587\times \left(1.19835\right)$

$\Rightarrow S_5=40.0914+0.04682$

$\Rightarrow S_5=40.13822$.

The graph of trajectories for $\sigma =0.25$ is as shown in the below figure:

Since the approximation in the graph of trajectories for $\sigma =0.1$ is better than the graph of trajectories for $\sigma =0.25$.

Therefore, for $\sigma =0.25$, the degree of variability is greater than the degree of variability for $\sigma =0.1$.