
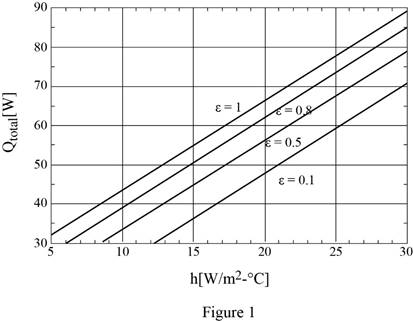
The plotting of rate of heat transfer against the convection heat transfer coefficient for the surface emissivities of 0.1, 0.5, 0.8, and 1. Also, discuss the results.
Answer to Problem 100P
The plotting of rate of heat transfer against the convection heat transfer coefficient for the surface emissivities of 0.1, 0.5, 0.8, and 1 are shown in Figure (1) and results are discussed as below.
Explanation of Solution
Calculate the rate of heat transfer by convection.
Here, change in the temperature is
Calculate the rate of heat transfer by radiation.
Here, surface temperature is
Calculate the total rate of heat transfer from the ball.
Conclusion:
Let us solve for
Substitute
Substitute
Substitute 34.35 W for
Follow the above process to calculate the rate of heat transfer against the convection heat transfer coefficient for the surface emissivities of 0.1 and 0.5 using spreadsheet including equations (I), (II), and (III) as in table (1).
| 5 | 11.4511 | 2.04127 | 13.4924 | 10.2064 | 21.6575 |
| 7.5 | 17.1767 | 2.04127 | 19.2179 | 10.2064 | 27.383 |
| 10 | 22.9022 | 2.04127 | 24.9435 | 10.2064 | 33.1086 |
| 12.5 | 28.6278 | 2.04127 | 30.669 | 10.2064 | 38.8341 |
| 15 | 34.3533 | 2.04127 | 36.3946 | 10.2064 | 44.5597 |
| 17.5 | 40.0789 | 2.04127 | 42.1201 | 10.2064 | 50.2852 |
| 20 | 45.8044 | 2.04127 | 47.8457 | 10.2064 | 56.0108 |
| 22.5 | 51.53 | 2.04127 | 53.5712 | 10.2064 | 61.7363 |
| 25 | 57.2555 | 2.04127 | 59.2968 | 10.2064 | 67.4619 |
| 27.5 | 62.9811 | 2.04127 | 65.0224 | 10.2064 | 73.1874 |
| 30 | 68.7066 | 2.04127 | 70.7479 | 10.2064 | 78.913 |
Continue table (1) for
| 16.3302 | 27.7813 | 20.4127 | 31.8638 |
| 16.3302 | 33.5068 | 20.4127 | 37.5894 |
| 16.3302 | 39.2324 | 20.4127 | 43.3149 |
| 16.3302 | 44.9579 | 20.4127 | 49.0405 |
| 16.3302 | 50.6835 | 20.4127 | 54.766 |
| 16.3302 | 56.4091 | 20.4127 | 60.4916 |
| 16.3302 | 62.1346 | 20.4127 | 66.2172 |
| 16.3302 | 67.8602 | 20.4127 | 71.9427 |
| 16.3302 | 73.5857 | 20.4127 | 77.6683 |
| 16.3302 | 79.3113 | 20.4127 | 83.3938 |
| 16.3302 | 85.0368 | 20.4127 | 89.1194 |
Show the plotting of rate of heat transfer against the convection heat transfer coefficient for the surface emissivities of 0.1, 0.5, 0.8, and 1.0 using Table (1) and (2) as in Figure (1).
Want to see more full solutions like this?
Chapter 2 Solutions
THERMODYNAMICS: ENG APPROACH LOOSELEAF
- (Manning equation) The triangular flume shown in the figure below is built to carry its design flowrate, Qo, at a depth of 0.991 m as is indicated. If the flume is to be able to carry up to twice its design flowrate, Q = 2Qo, determine the freeboard, I, needed. ✓ -90°- 0.991 m i marrow_forwardWater flows in a 2-ft-wide rectangular channel at a rate of 10 ft³/s. If the water depth downstream of a hydraulic jump is 2.5 ft, determine (a) the water depth upstream of the jump, (b) the upstream and (c) downstream Froude numbers, and (d) the head loss across the jump. (a) y₁ = i (b) Fr₁ = i (c) Fr₂ = i (d) h₁ = ft ftarrow_forwardA hydraulic jump at the base of a spillway of a dam is such that the depths upstream and downstream of the jump are 0.8 and 3.2 m, respectively (see the Video). If the spillway is 12 m wide, what is the flowrate over the spillway? Q= i m³/sarrow_forward
- (Manning equation) Water flows in a rectangular channel of width b at a depth of b/2. Determine the diameter of a circular channel (in terms of b) that carries the same flowrate when it is half-full. Both channels have the same Manning coefficient, n, and slope. barrow_forward(Manning equation) A weedy irrigation canal of trapezoidal cross section is to carry 20 m³/s when built on a slope of 0.60 m/km. If the sides are at a 45° angle and the bottom is 8 m wide, determine the width of the waterline at the free surface. i marrow_forwardWater flows in a 1.2-m-diameter finished concrete pipe so that it is completely full and the pressure is constant all along the pipe. If the slope is So = 0.0073, (a) determine the flowrate by using open-channel flow methods. Compare this result with (b) that obtained using the pipe flow methods of Chapter 8 (Use Colebrook formula, Table 8.1, Table 10.1 and assume that Re > 10º). (a) Q = i (b) Q = i m³/s m³/sarrow_forward
- for this 4 figuredarw the Kinematic Diagram:DoF:F=Type/Name ofmechanismEvolution:arrow_forwardTwo channels and two plates are used to formthe column section shown. For b = 200 mm,determine the moments of inertia and theradii of gyration of the combined section withrespect to the centroidal x and y axes.For the section of problem, determine thefirst moment of the upper plate about thecentroidal x-axisarrow_forwardDetermine by direct integration the moment of inertia of theshaded area at right with respect to the x axis shown. Determine by direct integration the moment of inertia of theshaded area of the figure with respect to the y axis shown.arrow_forward
- For the following MATLAB code, I need to answer a few questions. Can you identify the curves as elliptic functions? Which curves reflect the sn, cn, and dn functions?From the curves, determine the maximum amplitudes and the period corresponding toeach angular velocity component. clc; clear all; I = [500; 125; 425]; w = [0.2; 0.1; 0.2]; rev = 0:0.01:10; C = eye(3); % Using ode45 to integrate the KDE and DDE options = odeset('RelTol',1e-9,'AbsTol',1e-9); result = ode45(@K_DDE, rev, [w; I; C(:)], options); v = result.x; % Extracting information from the ode45 solver w = result.y(1:3, :); C_ode = reshape(result.y(7:end, :), [3,3,length(v)]); plot(v, w) xlabel('rev') ylabel('w (rad/s)') legend('w1', 'w2', 'w3') % Functions function dwCdt = K_DDE(~, w_IC) % Extracting the initial condtions to a variable w = w_IC(1:3); I = w_IC(4:6); C = reshape(w_IC(7:end), [3, 3]); I1 = I(1); I2 = I(2); I3 = I(3); K1 = -(I3-I2)/I1; K2 = -(I1-I3)/I2; K3 = -(I2-I1)/I3; %…arrow_forwardplease show a drawing/image and explain how to properly do the question. thanksarrow_forwardFor the four-bar- linkage shown in the following figure. BC=68mm, CD=100mm, AD=120mm. Determine the range of AB to make it a crank-rocker mechanism. B Darrow_forward
 Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
