Chapter 27, Problem 22P

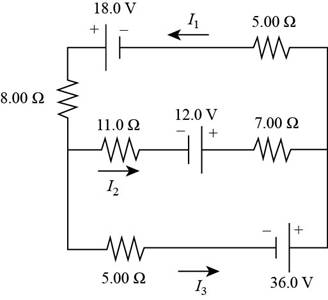
For the circuit shown in Figure P27.22, we wish to find the currents I₁, I₂, and I₃. Use Kirchhoff’s rules to obtain equations for (a) the upper loop, (b) the lower loop, and (c) the junction on the left side. In each case, suppress units for clarity and simplify, combining the terms. (d) Solve the junction equation for I₃. (e) Using the equation found in part (d), eliminate I₃ from the equation found in part (b). (f) Solve the equations found in parts (a) and (e) simultaneously for the two unknowns I₁ and I₂. (g) Substitute the answers found in part (f) into the junction equation found in part (d), solving for I₃. (h) What is the significance of the negative answer for I₂?

Figure P27.22

To determine

The equation by using Kirchhoff’s rules in the upper loop.

Answer to Problem 22P

The equation by using Kirchhoff’s rules in the upper loop is $\left(13.008\Omega \right)I_1+\left(18.0\Omega \right)I_2=30.0\text{V}$.

Explanation of Solution

Given info: The figure is given as,

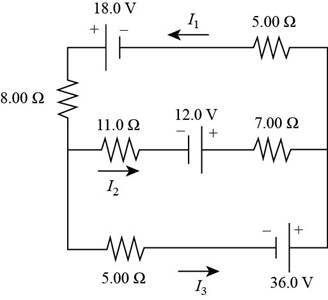
By going counterclockwise around the upper loop and suppressing the unites, the Kirchhoff’s law is applied.

The equation for the upper loop is,

$\begin{array}{c}\left[\begin{array}{l}-\left(11.0\Omega \right)I_2+12.0\text{V}-\left(7.00\Omega \right)I_2\\ -\left(5.00\Omega \right)I_1+18.0\text{V}-\left(8.00\Omega \right)I_1\end{array}\right]=0\\ \left(13.0\Omega \right)I_1+\left(18.0\Omega \right)I_2=30.0\text{V}\end{array}$ (1)

Conclusion:

Therefore, the equation by using Kirchhoff’s rules in the upper loop is $\left(13.008\Omega \right)I_1+\left(18.0\Omega \right)I_2=30.0\text{V}$.

To determine

The equation by using Kirchhoff’s rules in the lower loop.

Answer to Problem 22P

The equation by using Kirchhoff’s rules in the lower loop is $\left(18.0\Omega \right)I_2-\left(5.00\Omega \right)I_3=-24.0\text{V}$.

Explanation of Solution

Given info: The figure is given as,

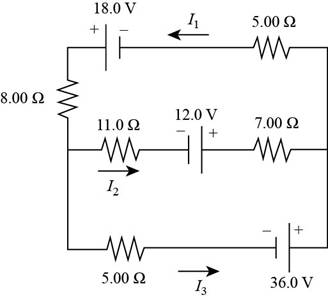
By going counterclockwise around the lower loop and suppressing the unites, the Kirchhoff’s law is applied.

The equation for the lower loop is,

$\begin{array}{c}\left[\begin{array}{l}-\left(5.00\Omega \right)I_3+36.0\text{V}+\left(7.00\Omega \right)I_2\\ -12.0\text{V}+\left(11.0\Omega \right)I_2\end{array}\right]=0\\ \left(18.0\Omega \right)I_2-\left(5.00\Omega \right)I_3=-24.0\text{V}\end{array}$ (2)

Conclusion:

Therefore, the equation by using Kirchhoff’s rules in the lower loop is $\left(18.0\Omega \right)I_2-\left(5.00\Omega \right)I_3=-24.0\text{V}$.

To determine

The equation by using Kirchhoff’s rules at the junction on the left side.

Answer to Problem 22P

The equation by using Kirchhoff’s rules at the junction on the left side is $I_1-I_2-I_3=0$.

Explanation of Solution

Given info: The figure is given as,

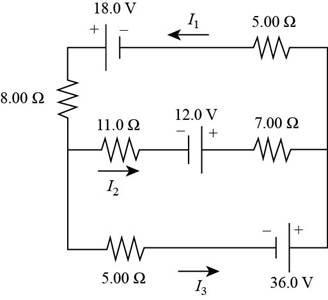
Apply the junction rule at the node in the left end of the circuit.

The equation for the junction on the left side is,

$I_1-I_2-I_3=0$ (3)

Conclusion:

Therefore, the equation by using Kirchhoff’s rules at the junction on the left side is $I_1-I_2-I_3=0$.

To determine

To solve: The junction on the left side for $I_3$.

Answer to Problem 22P

The junction on the left side for $I_3$ is $I_1-I_2$.

Explanation of Solution

Given info: The figure is given as,

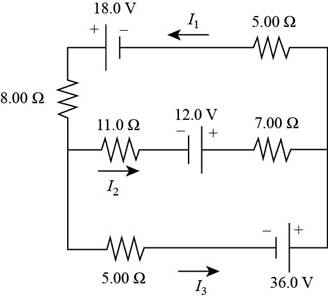
Apply the junction rule at the node in the left end of the circuit.

Rearrange the equation (3) as,

$\begin{array}{c}{I}_1-I_2-I_3=0\\ I_3=I_1-I_2\end{array}$

Conclusion:

Therefore, the junction on the left side for $I_3$ is $I_1-I_2$.

To determine

To eliminate: The current $I_3$ from the equation of part (b) by using equation of part (d).

Answer to Problem 22P

The equation after elimination\ for $I_3$ is $\left(5.00\Omega \right)I_1-\left(23.0\Omega \right)I_2=24.0\text{V}$.

Explanation of Solution

Given info: The figure is given as,

The equation for $I_3$ is,

$I_3=I_1-I_2$

Substitute $I_1-I_2$ for $I_3$ in equation (2).

$\begin{array}{c}\left(18.0\Omega \right)I_2-\left(5.00\Omega \right)\left(I_1-I_2\right)=-24.0\text{V}\\ \left(18.0\Omega \right)I_2-\left(5.00\Omega \right)I_1+\left(5.00\Omega \right)I_2=-24.0\text{V}\\ \left(5.00\Omega \right)I_1-\left(23.0\Omega \right)I_2=24.0\text{V}\end{array}$ (4)

Conclusion:

Therefore, the equation after elimination for $I_3$ is $\left(5.00\Omega \right)I_1-\left(23.0\Omega \right)I_2=24.0\text{V}$.

To determine

The value of $I_1$ and $I_2$ from the equation of part (a) and part (e).

Answer to Problem 22P

The value of $I_1$ and $I_2$ from the equation of part (a) and part (e) is $2.88\text{A}$ and $-0.416\text{A}$ respectively.

Explanation of Solution

Given info: The figure is given as,

Rearrange the equation (4) for $I_1$.

$\begin{array}{c}\left(5.00\Omega \right)I_1-\left(23.0\Omega \right)I_2=24.0\text{V}\\ I_1=\frac{\left(24.0\text{V}\right)+\left(23.0\Omega \right)I_2}{\left(5.00\Omega \right)}\end{array}$ (5)

Recall the equation (1).

$\left(13.0\Omega \right)I_1+\left(18.0\Omega \right)I_2=30.0\text{V}$

Substitute $\frac{\left(24.0\text{V}\right)+\left(23.0\Omega \right)I_2}{\left(5.00\Omega \right)}$ for $I_1$ in above equation (1).

$\begin{array}{c}\left(13.0\Omega \right)\left(\frac{\left(24.0\text{V}\right)+\left(23.0\Omega \right)I_2}{\left(5.00\Omega \right)}\right)+\left(18.0\Omega \right)I_2=30.0\text{V}\\ \left(13.0\Omega \right)\left(\left(24.0\text{V}\right)+\left(23.0\Omega \right)I_2\right)+\left(5.00\Omega \right)\left(18.0\Omega \right)I_2=\left(5.00\Omega \right)\left(30.0\text{V}\right)\\ 312\Omega \cdot \text{V}+\left(299{\Omega }^2\right)I_2+\left(90{\Omega }^2\right)I_2=150\Omega \cdot \text{V}\\ \left(389{\Omega }^2\right)I_2=-162\Omega \cdot \text{V}\end{array}$

Further, solve,

$\begin{array}{c}\left(389{\Omega }^2\right)I_2=-162\Omega \cdot \text{V}\\ I_2=\frac{-162\Omega \cdot \text{V}}{\left(389{\Omega }^2\right)}\\ =-0.416\text{A}\end{array}$

Thus, the value of $I_2$ is $-0.416\text{A}$.

Substitute $-0.416\text{A}$ for $I_2$ in equation (5).

$\begin{array}{c}{I}_1=\frac{\left(24.0\text{V}\right)+\left(23.0\Omega \right)\left(-0.416\text{A}\right)}{\left(5.00\Omega \right)}\\ =2.88\text{A}\end{array}$

Conclusion:

Therefore, the value of $I_1$ and $I_2$ from the equation of part (a) and part (e) is $2.88\text{A}$ and $-0.416\text{A}$ respectively.

To determine

The value of $I_3$.

Answer to Problem 22P

The value of $I_3$ is $3.29\text{A}$.

Explanation of Solution

Given info: The figure is given as,

The equation for $I_3$ is,

$I_3=I_1-I_2$

Substitute $2.88\text{A}$ for $I_1$ and $-0.416\text{A}$ for $I_3$ in above equation to find $I_3$.

$\begin{array}{c}{I}_3=\left(2.88\text{A}\right)-\left(-0.416\text{A}\right)\\ =3.29\text{A}\end{array}$

Conclusion:

Therefore, the value of $I_3$ is $3.29\text{A}$.

To determine

The significant of the negative sign of answer of $I_2$.

Answer to Problem 22P

The negative sign in the answer for $I_2$ means that this current flows in the opposite direction.

Explanation of Solution

Given info: The figure is given as,

The negative sign in the answer for $I_2$ means that this current flows in the opposite direction to that shown in the circuit diagram. That is the actual current in the middle branch of the circuit flows from right to left and has a magnitude of $0.416\text{A}$.

Conclusion:

Therefore, the negative sign in the answer for $I_2$ means that this current flows in the opposite direction.